Algebraic Division
Algebraic Division Revision
Algebraic Division
Algebraic division is the process of dividing a polynomial by a linear expression. It’s useful as it breaks down complex polynomials into easier ones.
There are some key terms that you need to understand first:
- Degree – the highest power in a polynomial.
- Divisor – the thing you are dividing by.
- Quotient – what you get when you divide by a divisor (it includes the remainder).
- Remainder – what is left over (this will be a constant in A level Maths).
There are 3 methods for algebraic division that you will see.
Make sure you are happy with the following topics before continuing.
The Factor Theorem
The Factor Theorem is defined as:
“If f(x) is a polynomial, and f(k)=0, then (x-k) is a factor of f(x)”
or
“If f \left(\dfrac{b}{a} \right)=0, then (ax-b) is a factor of f(x)”
i.e. if you know the roots then you know the factors, and if you know the factors then you know the roots.
Method 1: Subtracting Multiples of the Divisor
This method uses the following procedure:
Step 1: Subtract a multiple of (x-k) to cancel the highest power of x.
Step 2: Repeat Step 1, until there are no powers of x remaining.
Step 3: Work out how many lots of (x-k) you subtracted, and write this as an expression with the remainder.
Example: Divide 2x^3 - 5x^2 + 4x - 3 by \textcolor{limegreen}{(x-3)}
Step 1: Subtract 2x^2 lots of x-3, so that the x^3 term is cancelled:
(2x^3 - 5x^2 + 4x - 3) - \textcolor{red}{2x^2}\textcolor{limegreen}{(x-3)} = (2x^3 - 5x^2 + 4x - 3) - 2x^3 + 6x^2 = x^2+ 4x - 3
Step 2: Repeat this process, to remove all powers of x.
Start subtracting x lots of x-3 to remove the x^2 term in x^2 + 4x - 3:
(x^2 + 4x - 3) - \textcolor{red}{x}\textcolor{limegreen}{(x-3)} = (x^2 + 4x - 3) - x^2 + 3x = 7x - 3
Then, subtract 7 lots of (x-3) to remove the x term:
(7x-3) - \textcolor{red}{7}\textcolor{limegreen}{(x-3)} = (7x-3) - 7x + 21 = \textcolor{blue}{18}
Step 3: In total, we have subtracted \textcolor{red}{2x^2 + x + 7} lots of \textcolor{limegreen}{(x-3)}, and there is \textcolor{blue}{18} left over.
So,
(2x^3 - 5x^2 + 4x - 3) \div \textcolor{limegreen}{(x-3)} = \textcolor{red}{2x^2 + x + 7} remainder \textcolor{blue}{18}
Method 2: Algebraic Long Division
This method uses the same principles as long division for numbers, but for algebraic expressions.
Example: Divide x^3 + 6x^2 - 11x + 4 by \textcolor{limegreen}{(x-2)}
Step 1: Divide x^3 by x to get \textcolor{red}{x^2}, and put this at the top
Step 2: Multiply x^2 by \textcolor{limegreen}{(x-2)} to get x^3 - 2x^2
Step 3: Subtract to get 8x^2 and bring the -11x down
Step 4: Divide 8x^2 by x to get \textcolor{red}{8x}, and put this at the top
Step 5: Multiply 8x by \textcolor{limegreen}{(x-2)} to get 8x^2 - 16x
Step 6: Subtract to get 5x and bring the +4 down
Step 7: Divide 5x by x to get \textcolor{red}{5}, and put this at the top
Step 8: Multiply 5 by \textcolor{limegreen}{(x-2)} to get 5x-10
Step 9: Subtract to get \textcolor{blue}{14}, which is the remainder – since this term has a degree that’s less than the divisor, therefore it can’t be divided.
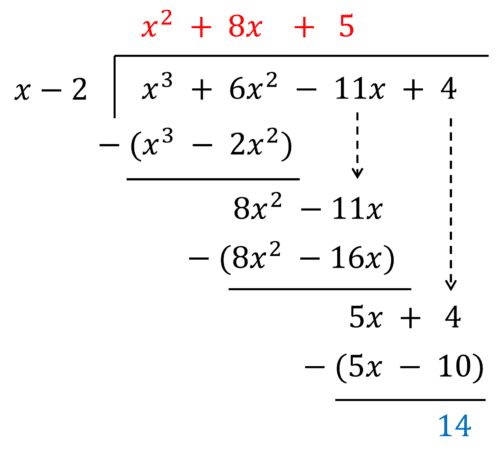
Hence,
(x^3 + 6x^2 - 11x + 4) \div \textcolor{limegreen}{(x-2)} = \textcolor{red}{x^2 + 8x + 5} remainder \textcolor{blue}{14}
Note: If the polynomial you are dividing doesn’t have an x^2 term for example, just put 0x^2 where the x^2 usually goes.
Method 3: Using a Formula
This method makes use of the following identity.
“A polynomial, f(x), can be written as
f(x) \equiv q(x)d(x) + r(x)
where q(x) is the quotient, d(x) is the divisor and r(x) is the remainder.”
You then use the following procedure:
Step 1: Find the degrees of the quotient and remainder. The degree of the quotient is \text{deg } f(x) - \text{deg } d(x). For the degree of the remainder, \text{deg } r(x) < \text{deg } d(x).
Step 2: Write the division in the form above, replacing q(x) and r(x) with general polynomials (i.e. Ax^2 + Bx + C is a general polynomial of degree 2)
Step 3: Find the values of the constants A, B and C etc., by substituting in values for x and equating coefficients.
Step 4: Replace A, B and C etc. in the general polynomial with the values you have just found.
Example: Divide x^3 + 4x^2 + 6x + 8 by \textcolor{orange}{(x+2)}
Step 1: This polynomial has degree 3, since the highest power if x is 3, and the divisor has degree 1. Therefore the quotient has degree 3-1=2 (so it is a quadratic). The remainder has degree 0.
Step 2: Write the division in the form f(x) \equiv q(x)d(x) + r(x):
x^3 + 4x^2 + 6x + 8 \equiv (Ax^2 + Bx + C)\textcolor{orange}{(x+2)} + D
Step 3: Substitute x= -2 to make d(x)=0, therefore the q(x)d(x) part will disappear and will leave the remainder, D.
\begin{aligned} (-2)^3 + 4(-2)^2 +6(-2) + 8 &= D \\ 4 &= D \end{aligned}
Now, substitute D=4 and x=0 into the equation:
\begin{aligned} 8 &= 2C +4 \\ 2 &= C \end{aligned}
So, we have
\begin{aligned} &x^3 + 4x^2 + 6x + 8 \\ &\equiv (Ax^2 + Bx + 2)\textcolor{orange}{(x+2)} + 4 \\ &\equiv Ax^3 + (2A + B)x^2 + (2B+2)x + 8 \end{aligned}
Equating coefficients x^3, x^2 and x gives:
A = 1 and 2A + B = 4 so B = 2
Step 4: Put the values of \textcolor{purple}{A=1}, \textcolor{limegreen}{B=2}, \textcolor{blue}{C=2} and \textcolor{red}{D=4} into the identity, which gives
x^3 + 4x^2 + 6x + 8 \equiv (x^2 + \textcolor{limegreen}{2}x + \textcolor{blue}{2})\textcolor{orange}{(x+2)} + \textcolor{red}{4}
Hence,
(x^3 + 4x^2 + 6x + 8) \div \textcolor{orange}{(x+2)} = (x^2 + \textcolor{limegreen}{2}x + \textcolor{blue}{2}) remainder \textcolor{red}{4}
Note: For A level maths, you will only see questions involving \text{deg } d(x) = 1 and \text{deg } r(x) = 0
Note:
The Factor Theorem can be combined with the 3 methods for dividing polynomials, which will enable you to factorise cubics and quartics.
Example: The Factor Theorem
a) Show that (x-2) is a factor of f(x) = x^3 + 5x^2 - 19x + 10
[2 marks]
b) The polynomial g(x) = x^3 - 8x^2 + 11x + 20 has roots at x=4, x=5 and x=-1. Factorise g(x) completely.
[2 marks]
a) If f(2) = 0, then (x-2) is a factor of f(x) by the Factor Theorem.
f(2) = (2)^3 +5(2)^2 - 19(2) + 10 = 0
Hence, by the Factor Theorem, (x-2) is a factor of f(x).
b) By the Factor Theorem, if a is a root of g(x), then g(a) = 0. So (x-a) is a factor of g(x).
We’re given all the roots of the cubic, so we can factorise it using the Factor Theorem.
g(x) = x^3 - 8x^2 + 11x + 20 = (x-4)(x-5)(x+1)
Algebraic Division Example Questions
Question 1: Determine whether (3x-1) is a factor of f(x) = 3x^3 + 8x^2 - 15x + 4
[2 marks]
Use the factor theorem with a =3 and b = 1
If f \left( \dfrac{1}{3} \right)=0, then (3x-1) is a factor of f(x)
f \left( \dfrac{1}{3} \right) = 3 \left( \dfrac{1}{3} \right)^3 + 8 \left( \dfrac{1}{3} \right)^2 - 15 \left(\dfrac{1}{3} \right) + 4 = 0
Hence, (3x-1) is a factor of f(x)
Question 2:
a) Determine whether (x+1) is a factor of f(x) = 2x^3 + 7x^2 + 2x - 3
b) Fully factorise f(x).
[5 marks]
a) Use the Factor Theorem with a = -1
If f(-1)=0 then (x+1) is a factor of f(x).
f(-1) = 2(-1)^3 + 7(-1)^2 + 2(-1) - 3 = 0
Hence, by the Factor Theorem, (x+1) is a factor of f(x).
b) (x+1) is a factor of f(x), so divide f(x) = 2x^3 + 7x^2 + 2x - 3 by (x+1)
(2x^3 + 7x^2 + 2x - 3) - 2x^2(x+1) \\ = (2x^3 + 7x^2 + 2x - 3) - 2x^3 - 2x^2 \\ = 5x^2 + 2x - 3
(5x^2 + 2x - 3) - 5x(x+1) \\ = (5x^2 + 2x - 3) - 5x^2 - 5x \\ = -3x - 3
(-3x - 3) - (-3(x+1)) \\ = (-3x - 3) + 3x + 3 = 0
So,
2x^3 + 7x^2 + 2x - 3 = (x+1)(2x^2 + 5x - 3)
Then, factorise the quadratic:
(2x^2 + 5x - 3) = (2x-1)(x+3)
Hence,
2x^3 + 7x^2 + 2x - 3 = (x+1)(2x-1)(x+3)
Question 3: Write 2x^3 + 17x^2 + 37x + 18 in the form (Ax^2 + Bx + C)(x+5) + D, where A, B, C and D are constants to be found.
[3 marks]
Put x = -5 into both sides of the identity 2x^3 + 17x^2 + 37x + 18 \equiv (Ax^2 + Bx + C)(x+5) + D:
2(-5)^3 + 17(-5)^2 + 37(-5) + 18 = D
D = 8
Now, let x=0
18 = 5C + 8, so C = 2
Equate the coefficients of x^3 to get A=2
Equate the coefficients of x^2 to get 5A + B = 17, so B = 7
Hence,
2x^3 + 17x^2 + 37x + 18 = (2x^2 + 7x + 2)(x+5) + 8
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






