Standard Form
Standard Form Revision
Standard Form
Sometimes in biology, chemistry and physics, we have the deal with very large and very small numbers. Standard form is a way of expressing these numbers, and it saves you from having write out the numbers in their entirety. You will need to know how to convert normal numbers into standard form and vice versa.
What is Standard Form?
Standard form is always written as number between 1 and 10, multiplied by 10 to the power of a whole number. Here are some examples:
5.4 \times 10^7
6.2 \times 10^{-3}
1.1 \times 10^{23}
6.63 \times 10^{-34}
The positive powers indicate bigger numbers and the negative powers indicate smaller numbers.
Writing Numbers in Standard Form
It is useful to write both very small and very large numbers in standard form.
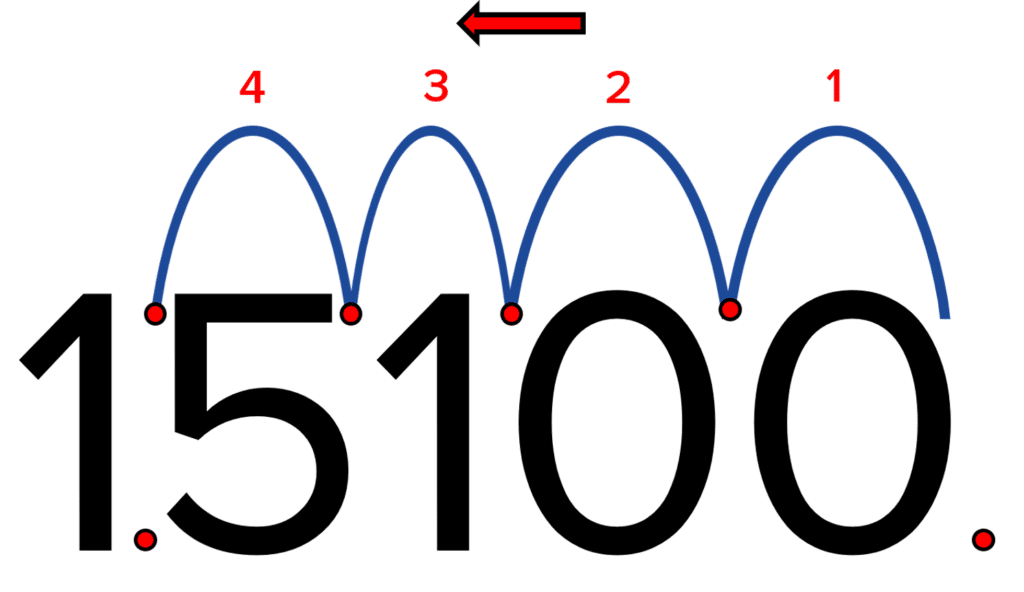

Example 1: Write 15 100 in standard form.
We need to write this as a number between 1 and 10. We know this must be 1.5. We can then count how many times the decimal place moves over:
The decimal place has moved over 4 times, from \boldsymbol{15100} to \boldsymbol{1.51}. The number of times the decimal moves over is the power. The power will be positive because the number is a big one (also because the decimal place has moved to the right). So the power will be positive 4. Therefore we can write 15100 as 1.51 \times 10^4.
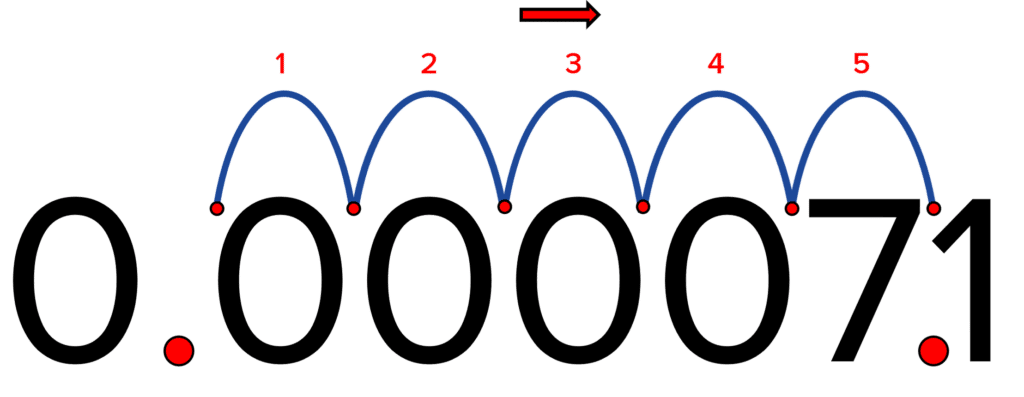

Example 2: Write 0.000071 in standard form.
We use the same method as the previous example. The number between 1 and 10 will be 7.1. We now count how many times we move the decimal place to get to 7.1:
The power is negative because the number is a small one (also because the decimal place has moved to the right). Therefore, 0.000071 in standard form is 7.1 \times 10^{-5}.
Converting from Standard Form
Converting from standard form is simple once you know how to write numbers in standard form. You simply count either forwards or back, moving the decimal place by the number of the power.
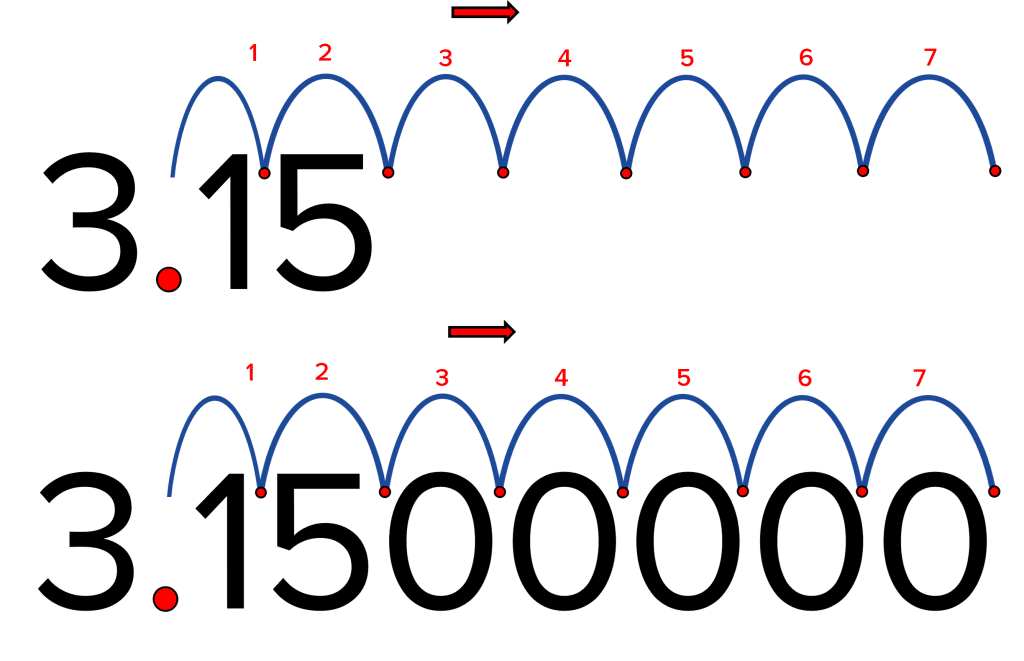

Example 1: Convert 3.15 \times 10^{7} from standard form.
The power is a positive 7 so need to move the decimal place 7 spaces up the number (to the right), and add zeros in the missing spaces:
Therefore 3.15 \times 10^7 converted from standard form is 31500000.


Example 2: Convert 6.78 \times 10^{-4} from standard form.
The power is a negative 4 so need to move the decimal place 4 spaces down the number (to the left) and add zeros in the missing spaces:
Therefore 6.78 \times 10^{-4} converted from standard form is 0.000678.
Standard Form Example Questions
Question 1: Write 52567 in standard form.
[1 mark]
Question 2: Write 0.009061 in standard form.
[1 mark]
Question 3: Determine which of the following numbers is larger.
5.36 \times 10^{-3}
7.82 \times 10^{-2}
[1 mark]
Converting each from standard form:
5.36 \times 10^{-3} = 0.00536
7.82 \times 10^{-2} = 0.0782
0.0782 > 0.00536 therefore 7.82 \times 10^{-2} is the larger number.

MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now