Volume
Volume Revision
Volume
Volume is a measure of how much space a 3\text{D} shape fills, just as area is a measure of how much 2\text{D} space a shape fills.
It is measured in distance cubed, so units of measurements are predominantly \text{cm}^3, \text{m}^3
Volume of Cubes and Cuboids
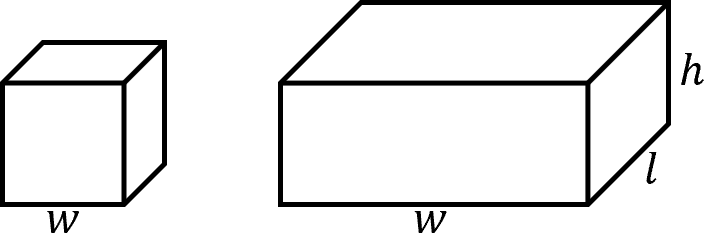
A cube has the same width, length and height in all dimensions, and as such, for a cube with width w, the volume of a cube is
\text{Volume of a Cube} = w^3
For a cuboid with, the width, height and length may all be different. So for a cuboid with a width, w, height, h and length, l, the volume of a cuboid is
\text{Volume of a Cuboid} = hlw
Volume of Prisms and Cylinders
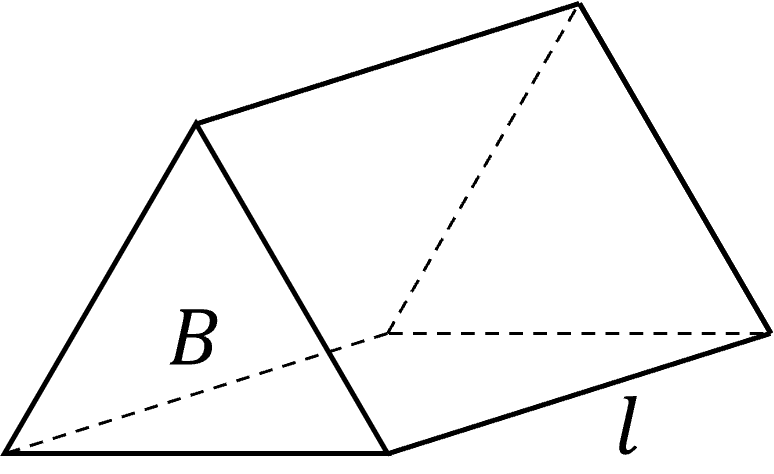

A prism is a 3\text{D} shape the same shape on both ends, connected by perpendicular edges. As if a 2\text{D} shape has been stretched into 3\text{D}.
Here is a triangular prism.
We call the shape of the ends of the prism, the base. The volume of a prism is related the area of it’s base and its length. If the area if the base is B, and the length is l, then the volume of a prism is
\text{Volume of a prism}= B\times l
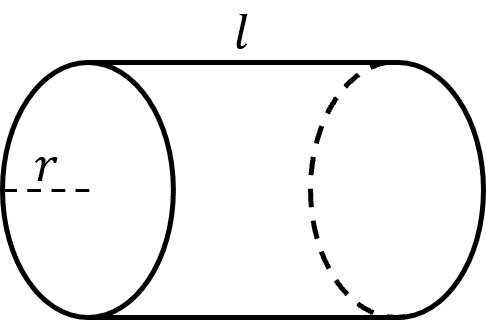

A cylinder is essentially a prism whose base is a circle. So it has a curved length joining the base and the top. Although the formula is essentially the same, only this time we can find the area of the base in terms of the circle’s radius.
For for a circle with radius, r, the area of the base, B is
B = \pi r^2
which is just the formula for the area of a circle. So the volume of a cylinder is
\text{Volume of a Cylinder} = \pi r^2l
Volume of Pyramids
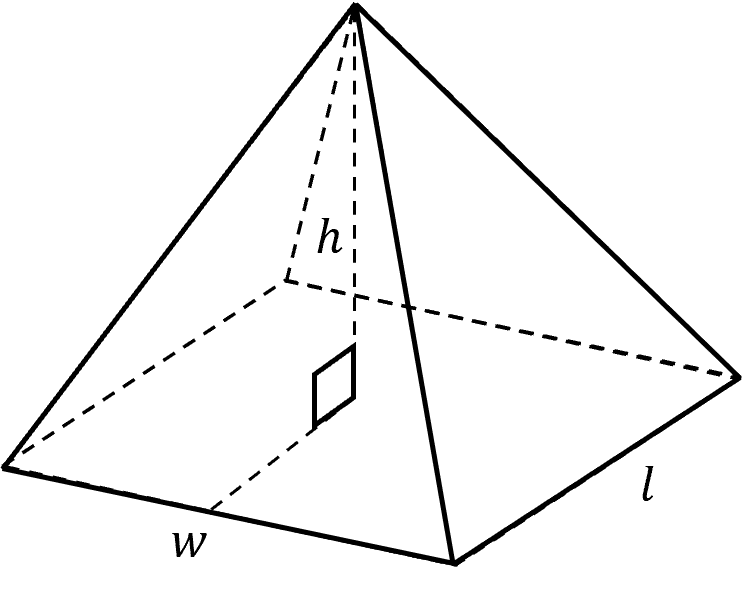

A pyramid is a 3\text{D} shape, with a 2\text{D} base, that shares edges with triangular faces the converge into a point. Once again, the volume is dependent on the area of the base, B and the height, h. The volume for a pyramid is
\text{Volume of a Pyramid} = \dfrac{1}{3} \times B \times h
So for a rectangular pyramid with width, w and length, l,
B = wl,
So
\text{Volume of a Rectangular Pyramid} = \dfrac{1}{3} \times w \times l \times h
Sometimes you may have the height of the triangles from their base edge to the peak, or the slant height, s. Then you may need to use Pythagoras theorem to find the height by constructing a right angle triangle, whose hypotenuse is the slant height, it’s height is the height of the pyramid.
For example with this rectangular pyramid, the front face may have a slant height of s, then the base of the constructed right angle triangle would be \dfrac{l}{2}, giving
h = \sqrt{s^2 - \left( \dfrac{l}{2}\right) ^2}
Volume of Cones
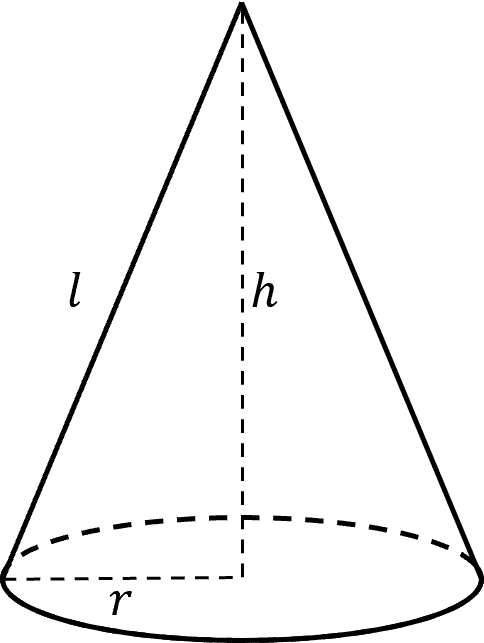

We may think of a cone as a pyramid with a circle for a base. In this sense, we can repurpose our equation for volume of a pyramid, only adapt it for a cone instead. Instead of a generic base, B, we can use the formula for the area of a circle, radius r,
B = \pi r^2
Then for a cone, with a height, h, we get the volume of a cone as
\text{Volume of a Cone} = \dfrac{1}{3} \times \pi r^2 \times h
Volume of Spheres
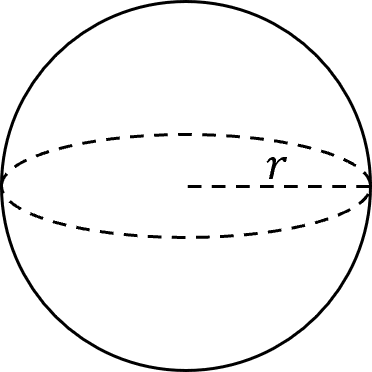

A sphere is a 3\text{D} shape that has the same radius from it’s centre to all points on the shapes surface. Which means the only variable to the volume of a sphere is it’s radius. So for a radius r, the volume of a sphere is
\text{Volume of a Sphere}= \dfrac{4}{3}\pi r^3
You may also be asked for the volume of a hemisphere, which is half of a sphere, just like how Earth is divided into the northern and southern hemispheres. The volume of a hemisphere is, sensibly, half that of a sphere.
\text{Volume of a Hemisphere} = \dfrac{2}{3} \pi r^3
Volume of Compound Shapes
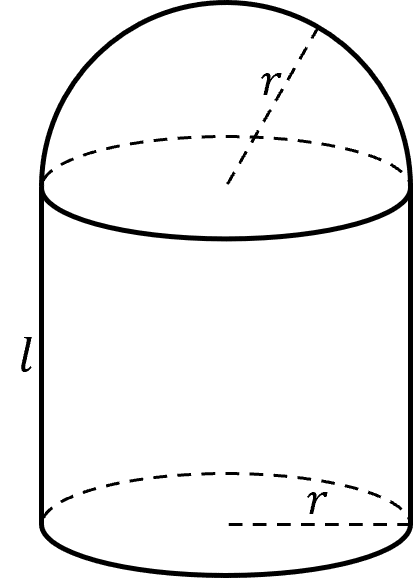

A compound shape is made up of other simpler shapes. So naturally, when measuring the amount of 3\text{D} space a shape fills, then the space filled by a compound shape is just the amount of space filled by the simpler shapes.
If a compound shape is made up of three 3\text{D} shapes, A, B and C, then the volume of the compound shape is simply
\text{Volume of the Compound Shape} = \text{Vol}(A) + \text{Vol}(B) + \text{Vol}(C)
Where \text{Vol}(A) is the volume of shape A and \text{Vol}(B) for shape B and so on.
Example 1: Finding the Volume of a Sphere
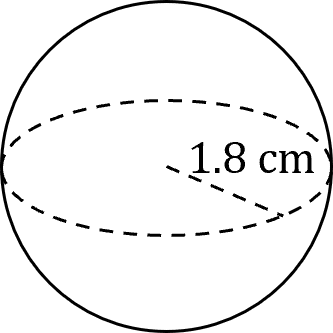

Find the volume of a sphere with a radius 1.8 \text{ cm}.
[3 marks]
We can simply use the equation, although it may be hard to remember. So let r = 1.8 \text{ cm}, then that gives the equation
\text{Volume} = \dfrac{4}{3}\pi \times 1.8^3
\text{Volume} = 7.776 \pi = 24.43 \text{ cm}^3
to 2 decimal places.
Example 2: Finding the Volume of a Cone
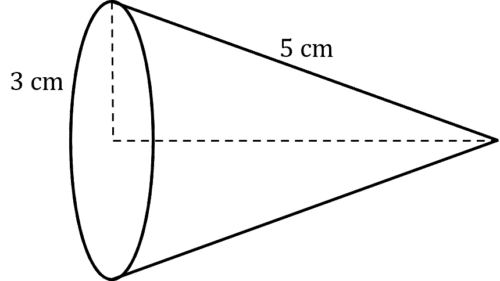
Find the volume of a cone with radius 3\text{ cm} and a slant length of 5\text{ cm}
[4 marks]
Well, first we need to find the real length of the cone. We can see that from the centre of the circle to the point on the cone is the real length, which means that we can construct a right angled triangle to find it.
This triangle will have a base of the length of the cone, l, and a height of the radius 3 \text{ cm}, which means that its hypotenuse is the slant height 5 \text{ cm}, so using Pythagoras
l = \sqrt{5^2-3^2}= \sqrt{16} = 4 \text{ cm}
Now, we can use the formula for the volume of a cone.
\text{Volume} = \dfrac{1}{3} \times \pi \times 3^2 \times 4
\text{Volume} = 12 \pi \text{ cm}^3
So the volume of the cone is 12 \pi \text{ cm}^3 or 37.7 \text{ cm}^3 to 1 decimal place.
Example 3: Finding the Volume of Compound Shapes
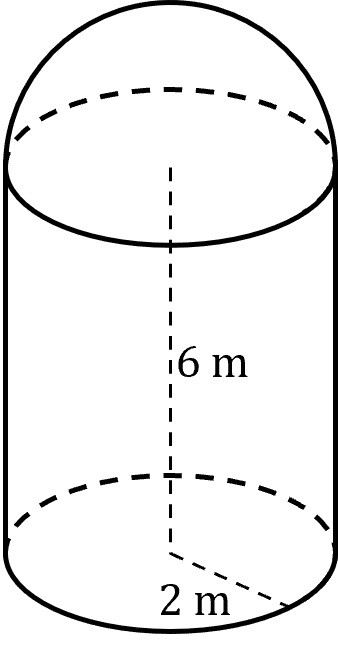

The top of a cylinder is adjoined to a hemisphere. The radius of the hemisphere and cylinder is 2\text{ m}, and the height of the cylinder is 6\text{ m}
Find the volume of the compound shape.
[5 marks]
A hemisphere is half a sphere, and so will have half the volume. The volume of the total compound shape will be the volume of the hemisphere plus the volume of the cylinder.
We can use the formula for the volume of a cylinder to find its volume. Let r = 2 \text{ m} and l = 6 \text{ m}, which gives us
\text{Cylinder volume} = \pi \times 2^2 \times 6 = 24 \pi \text{ m}^3
Now we can half the formula for the volume of a sphere to find the volume of the hemisphere, so letting r = 2 we get
\text{Hemisphere volume} = \dfrac{1}{2} \times \dfrac{4}{3}\pi r^3
\text{Hemisphere volume} =\dfrac{2}{3}\pi \times 2^3 = \dfrac{16\pi}{3}
Now we can add the two volumes to get
\text{Compound shape volume} = 24 \pi + \dfrac{16\pi}{3} = \dfrac{88\pi}{3}
\text{Compound shape volume} = 92.15 \text{ m}^3
to 2 decimal places.
Volume Example Questions
Question 1: This prism has an isosceles triangle for it’s base.
Work out the volume of the prism.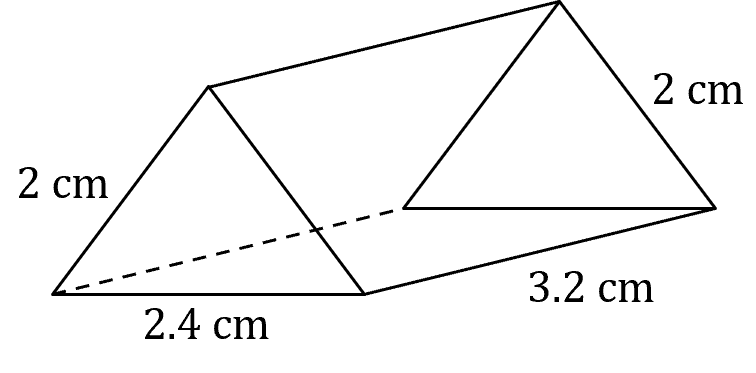
[3 marks]
Firstly, we must find the area of the base triangle. It is isosceles, with two edges of length 2\text{ cm} and one of length 2.4\text{ cm}. So we can split the isosceles into two right angle triangles to find the height of the triangle.
So there is a right angle triangle, with hypotenuse 2 \text{ cm} and a base of 1.2 \text{ cm}, using Pythagoras to find the height
\text{height}= \sqrt{2^2-1.2^2} = 1.6 \text{ cm}
So now he have the height the area of the triangle is
\text{Triangle area}= \dfrac{1}{2} \times 2.4 \times 1.6
\text{Triangle area}= 1.92 \text{ cm}^2
Now we can find the total volume.
\text{Volume} = 1.92 \times 3.2 = 6.144 \text{ cm}^3
Question 2: This pyramid has a right angle triangle as its base.
The pyramid has a height of 4 \text{ m}.
Work out the volume of the pyramid.
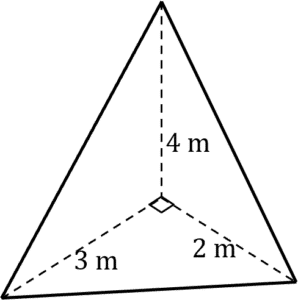
[3 marks]
Firstly we must find the area of the base, as it is a right angled triangle, its height is 3 \text{ m} and its width is 2 \text{ m}.
\text{Base area} = \dfrac{1}{2}\times 2 \times 3 = 3 \text{ m}^3
Now we can use the formula for the volume of a pyramid. So let B = 3 and h = 4, then
\text{Volume} = \dfrac{1}{3} \times 3 \times 4 = 4 \text{ m}^3
Question 3: A compound shape is made from a cone, with length 9 \text{ cm} and radius 3 \text{ cm}, and a hemisphere with the same radius.
Work out the volume of the compound shape.
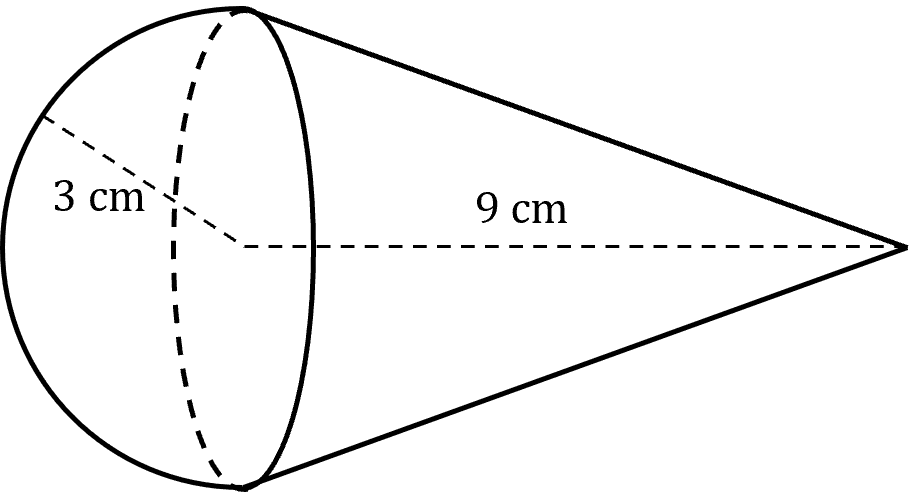
[5 marks]
Lets first find the volume of the hemisphere, which is half of the volume of a sphere with the same radius. This gives us
\text{Hemisphere volume} = \dfrac{1}{2} \times \dfrac{4}{3} \times 3^3 \pi
\text{Hemisphere volume} = 18 \pi
Now let’s find the volume of the cone, with the formula
\dfrac{1}{3} \times \pi 3^2 \times 9 = 27 \pi
So the total volume is
\text{Volume} = 18 \pi + 27 \pi = 45 \pi = 141.4 \text{ cm}^3
to one decimal place.







