Surface Area
Surface Area Revision
Surface Area
Surface area is the area of the outside of a 3\text{D} shape. If you picture the 3\text{D} shape, unfolded and placed flat out on a 2\text{D} surface, then the area of that shape is the surface area.
Surface Area of Cubes and Cuboids
The surface of a cube is made up of 6 square faces. The surface area of a cube is the sum of the area of the 6 squares.

For example, for a cube with side length \textcolor{red}{a}, each face has an area of \textcolor{red}{a}\times\textcolor{red}{a}=\textcolor{red}{a}^{2}, so the total surface area is:
\text{Surface Area of a Cube}=6\textcolor{red}{a}^{2}
A cuboid has six rectangular faces, which form three pairs of rectangles where opposite rectangles are identical.
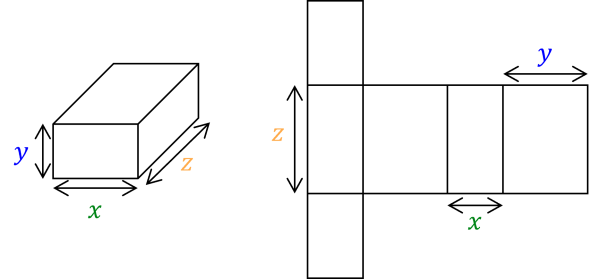
For example, for a cuboid with side lengths \textcolor{green}{x}, \textcolor{blue}{y} and \textcolor{orange}{z}, the areas of the rectangles are \textcolor{green}{x}\textcolor{blue}{y}, \textcolor{green}{x}\textcolor{orange}{z} and \textcolor{blue}{y}\textcolor{orange}{z}, with two of each type of rectangle. So the total surface area is:
\text{Surface Area of a Cuboid}=2(\textcolor{green}{x}\textcolor{blue}{y}+\textcolor{green}{x}\textcolor{orange}{z}+\textcolor{blue}{y}\textcolor{orange}{z})
Surface Area of Prisms and Cylinders
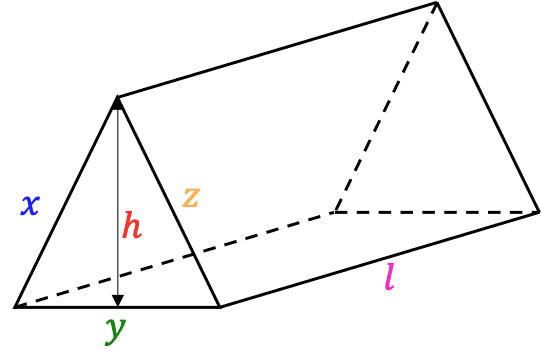

A prism is a type of 3\text{D} shape with a constant cross section. There are many different types such as a triangular prism, trapezoidal prism etc.
On the right is a triangular prism.
To find the surface area of a prism, imagine folding it out into a net. This results in two identical cross sections and a series of rectangles. The rectangles will all be the same length as the length of prism, but may vary in width. Summing the areas of these shapes results in the surface area.


Folding out this prism into its net results in the image on the right. We have three rectangles all of length \textcolor{magenta}{l}, but widths of \textcolor{blue}{x}, \textcolor{green}{y} and \textcolor{orange}{z} respectively. The two cross-sections from this shape are identical triangles of height \textcolor{red}{h} and base \textcolor{green}{y}.
The two triangles have an area of \dfrac{1}{2} \times \textcolor{green}{y} \times \textcolor{red}{h} each.
The rectangles have areas of \textcolor{blue}{x}\textcolor{magenta}{l}, \textcolor{green}{y}\textcolor{magenta}{l} and \textcolor{orange}{z}\textcolor{magenta}{l} respectively.
Thus, the total surface area is 2 \times \dfrac{1}{2} \textcolor{green}{y} \textcolor{red}{h} + \textcolor{blue}{x}\textcolor{magenta}{l} + \textcolor{green}{y}\textcolor{magenta}{l} +\textcolor{orange}{z}\textcolor{magenta}{l}= \textcolor{green}{y} \textcolor{red}{h} + \textcolor{blue}{x}\textcolor{magenta}{l} + \textcolor{green}{y}\textcolor{magenta}{l} +\textcolor{orange}{z}\textcolor{magenta}{l}
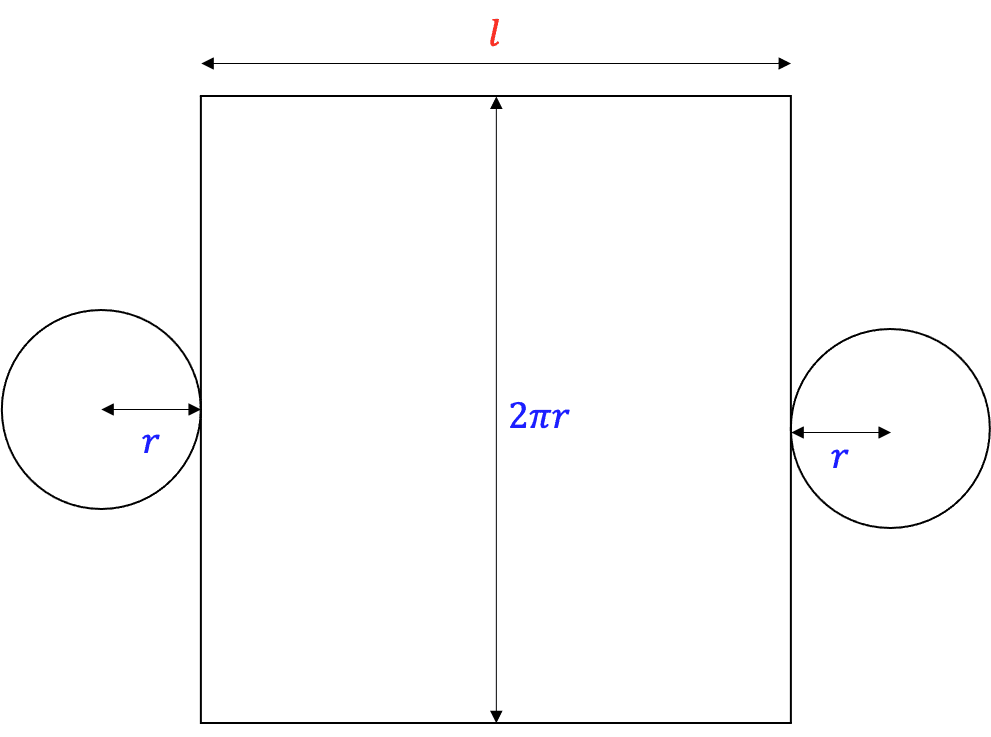

A cylinder is a prism whose base is a circle. So, to find the surface area we must fold it out into it’s net again. This results in the image on the right, two circles and a single rectangle. The rectangle shares the same length as the cylinder, while it’s width is the circumference of the circular cross-section.
Thus,
The rectangle’s width is \textcolor{blue}{2\pi r} where \textcolor{blue}{r} is the radius of the circular cross-section.
The rectangles area is then \textcolor{blue}{2\pi r} \times \textcolor{red}{l} =\textcolor{blue}{2\pi r}\textcolor{red}{l}
The area of each circle is \textcolor{blue}{\pi r^2}
Finally, the total surface area must be:
\text{Surface Area of a Cylinder} = 2\textcolor{blue}{\pi r^2} + \textcolor{blue}{2\pi r}\textcolor{red}{l} = 2\pi\textcolor{blue}{r} (\textcolor{blue}{r} + \textcolor{red}{l})
Surface Area of Pyramids
The surface area of a pyramid is the sum of the areas of the base and all of the triangular sides.
Recall: The formula for the area of a triangle is \dfrac{1}{2}\times\text{base}\times\text{height}
However, the height of the triangles is different to the height of the pyramid, because the triangles are slanted.
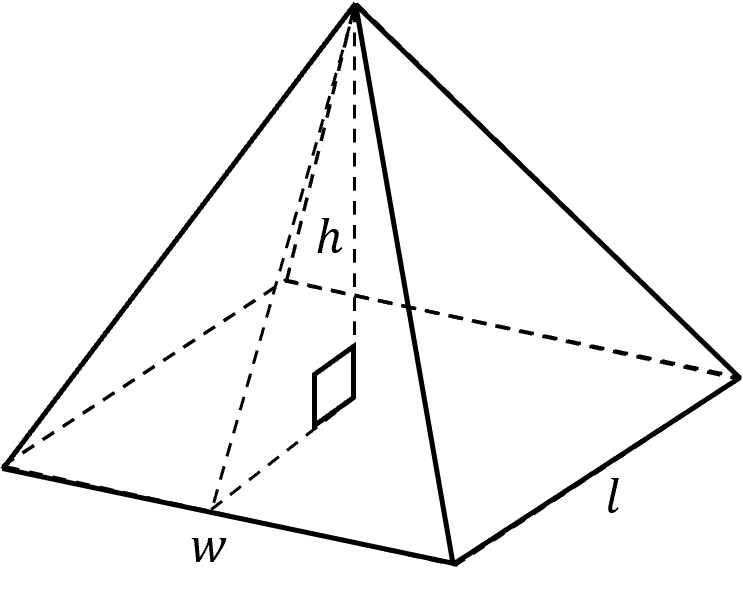

The image on the right shows a rectangular-based pyramid.
The area of the rectangular base is wl.
We can use Pythagoras’ Theorem to find the height of the triangle by constructing a right-angled triangle to the centre of the pyramid as pictured.
The width of this right-angled triangle to the centre is half the base length, so is \dfrac{l}{2}.
The height of this right-angled triangle is the height of the pyramid, h.
Hence, the height of the triangular face is: \sqrt{\left(\dfrac{l}{2}\right)^{2}+h^{2}}
And we can use this in the formula for the area of a triangle to give the area of the triangular face as:
\dfrac{1}{2}\times w\times \sqrt{\left(\dfrac{l}{2}\right)^{2}+h^{2}}
We can repeat this for all of the sides of the pyramid – however in most examples there will be many identical faces, for example for this rectangular based pyramid opposite triangles are identical so we only need to work out two triangle areas.
Then, we can add together the areas of all of the triangles, plus the area of the base, to find the surface area of the pyramid.
Surface Area of Cones
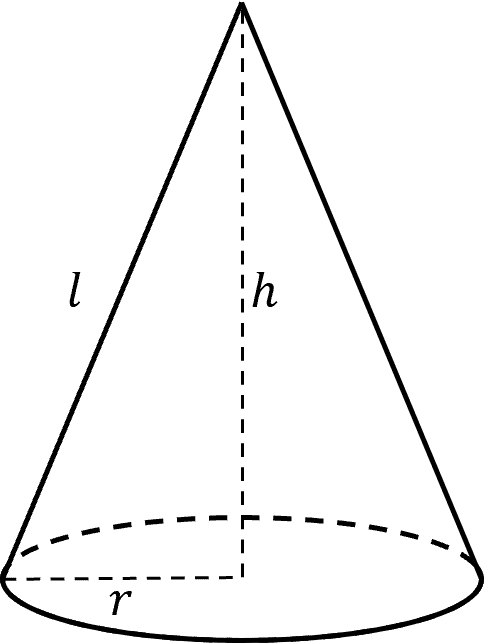

A cone is like a pyramid but with a circular base. The surface area of the pyramid is the area of the circular base added to the area of the curved surface. In the pictured example, the radius of the circle is r, the height of the cone is h and the slant height of the cone is l.
The area of the circular base is \pi r^{2}
The curved surface forms a circle sector when laid out flat, which has an area of \text{Area of the Curved Face} = \pi r l
Hence, the total surface area is:
\text{Surface area of a Cone}= \pi r^2 + \pi rl = \pi r (r+l)
Surface Area of Spheres
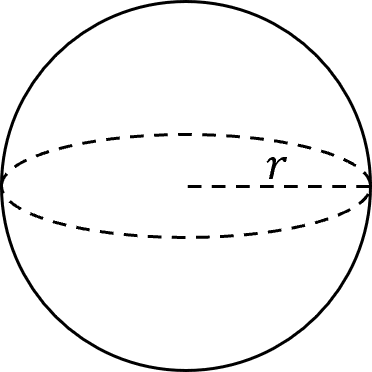

A sphere has no net, so you can’t work out its surface area by adding together the surface area of all the shapes in a net. However, the only variable in a sphere’s shape is the radius, r.
The formula to calculate the surface area of a sphere is:
\text{Surface Area of a Sphere}= 4\pi r^2
Surface Area of Compound Shapes
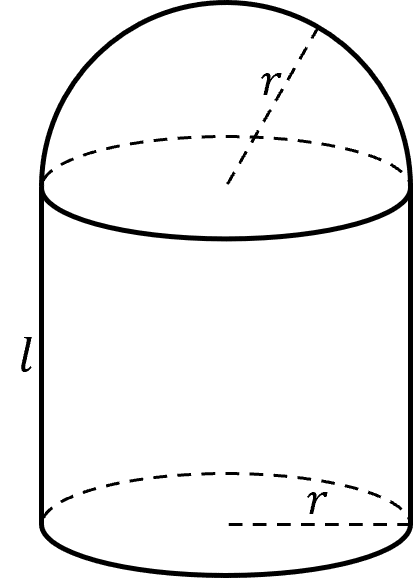

You will also be asked to give the surface area of 3\text{D} shapes made up of multiple other shapes called compound shapes. Here we have a hemisphere (half a sphere) attached to a cylinder of the same radius, r, with a length l.
The surface area of a hemisphere is half that of a sphere, plus the area of the base of the hemisphere, which is a circle, of the same radius.
\text{Surface Area of a Hemisphere}= 2 \pi r^2 + \pi r^2 = 3 \pi r^2
We already know the surface area of a cylinder is 2\pi r^2 +2\pi r l.
However we do not just add them together, as the base of the hemisphere and the top of the cylinder are not faces on the compound shape. So they must be subtracted from the combined surface area. The base of the hemisphere and the top of the cylinder have an area of \pi r^2, so 2\pi r^2 but be subtracted. Which gives us a surface area of
\text{Surface Area} = 3 \pi r^2 + 2\pi r^2 +2\pi r l -2\pi r^2
\text{Surface Area} = 3 \pi r^2 +2\pi r l
Example 1: Finding the Surface Area of Prisms
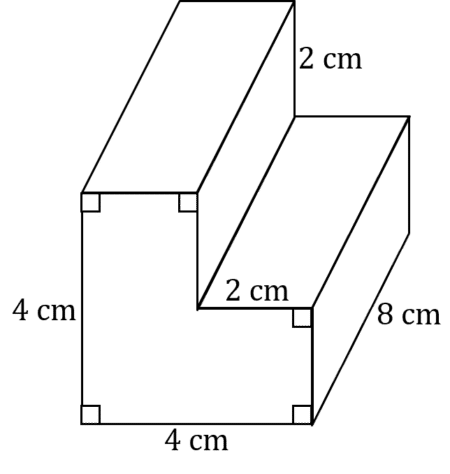
Work out the total surface area of this L-shaped prism.
[4 marks]
Firstly we must look at the base of the prism, the L-shape. We can look at it as two quadrilaterals connected, one being a 4\text{ cm} \times 2\text{ cm} rectangle, and a 2\text{ cm} \times 2 \text{ cm}, which gives us
\text{Area of the Square} = 2\times 2 = 4 \text{ cm}^2
\text{Area of the Rectangle} = 2\times 4 = 8 \text{ cm}^2
\text{Area of the L-shape} = 8+4 = 12 \text{ cm}^2
So now we must find the perimeter of the L-shape.
\text{Perimeter of the L-shape} = 2+2+2+2+4+4=16 \text{ cm}
We may now use the equation to find the total surface area of the prism. The length of the prism is 8\text{ cm}, so
\text{Surface Area of the Prism} = 2\times 12 + 8\times 16 = 152 \text{ cm}^2
Example 2: Finding the Surface Area of a Cylinder
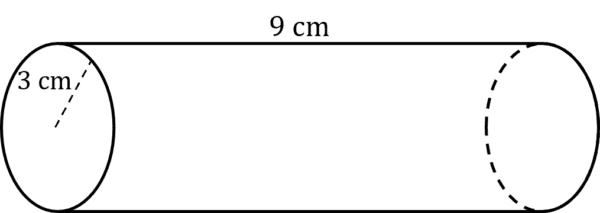
Work out the total surface area of this cylinder.
[3 marks]
As we know
\text{Surface Area of a Cylinder}= 2\pi r^2 +2\pi r l
and r=3 \text{ cm} and l = 9\text{ cm}, that gives us
\text{Surface Area the Cylinder}= 2\times 3^2 \pi +2 \times 3 \times 9 \pi
\text{Surface Area the Cylinder}= 18 \pi +54 \pi = 72 \pi
The surface area of the cylinder is 72 \pi \text{ cm}^2, or 226.19\text{ cm}^2 to 2 decimal place.
Example 3: Finding the Surface Area of Compound Shapes
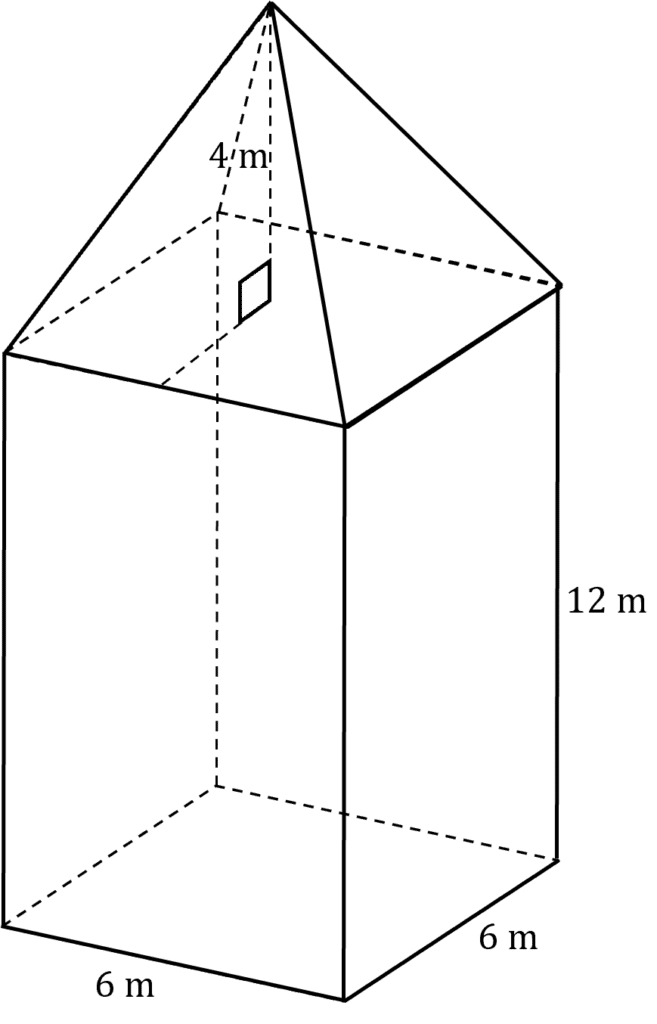

The compound shape is a cuboid with a square base pyramid fitted atop. The height of the square base pyramid is 4 \text{ m}, find the surface area of the shape.
[5 marks]
We start with the square base
\text{Area of the Square Base} = 6 \times 6 = 36\text{ m}^2
Now, the rectangular faces of the cuboid
\text{Area a Rectangular Face} = 6 \times 12 = 72 \text{ m}^2
Now we must find the area of the triangle faces of the square base pyramid. To do so, we must find their height, from the height of the pyramid. The pyramid is 4\text{ m} from the centre of it’s square base, and the centre of the square base is \dfrac{6}{2} = 3\text{ m} from the base of the triangle face. This now allows us to construct a right angled triangle, whose hypotenuse is the height of the triangle face. Giving us
\text{Slant Height of the Pyramid} = \sqrt{4^2 + 3^2}= 5 \text{ m}
Now the area of a triangle face is
\text{Area of a Triangle Face}= \dfrac{1}{2}\times 6 \times 5
\text{Area of a Triangle Face}= 15\text{ m}^2
Now, there are 4 rectangular faces, 4 triangular faces and 1 square face, giving us
\text{Surface Area}= 4\times 15 + 4 \times 72 + 36
\text{Surface Area}= 384 \text{ m}^2
Surface Area Example Questions
Question 1: Find the surface area of this triangular prism.
Give your answer to 2 decimal places.
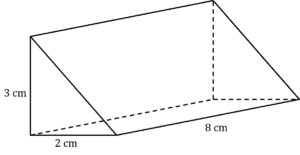
[3 marks]
The area of the triangle bases is
\dfrac{1}{2} \times 3\times 2 = 3 \text{ cm}^2
The hypotenuse of the triangle is
\sqrt{2^2+3^2}= \sqrt{13} \text{ cm}
Then the perimeter of the triangle is 5 +\sqrt{13} \text{ cm}, so the surface area of the prism is
\text{Surface Area} = 2 \times 3 + (5 +\sqrt{13}) \times 8
\text{Surface Area} =74.84 \text{ cm}^2
to 2 decimal places.
Question 2: Find the surface area of this cone.
Give your answer in terms of \pi.
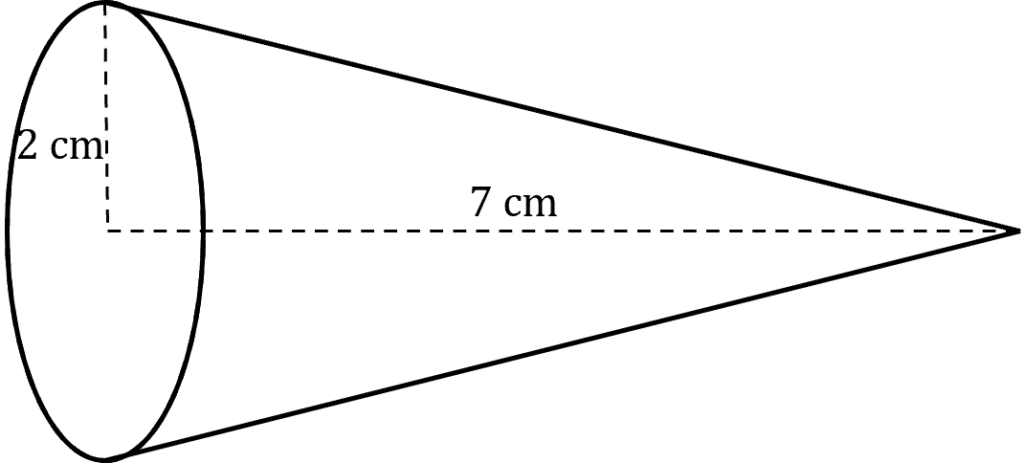
[ 3 marks]
Radius of the cone is 2 \text{ cm} and the length of the cone is 7 \text{ cm}, so using the formula for surface area of a cone
\text{Surface Area}= \pi \times 2( 2+7)
\text{Surface Area}= 18 \pi \text{ cm}^2
Question 3: This compound shape is a cylinder with radius 1.5 \text{m} and length 4.5 \text{m} attached to a cone length 5\text{m} with the same radius.
Find it’s surface area.
Give your answer in terms of \pi.
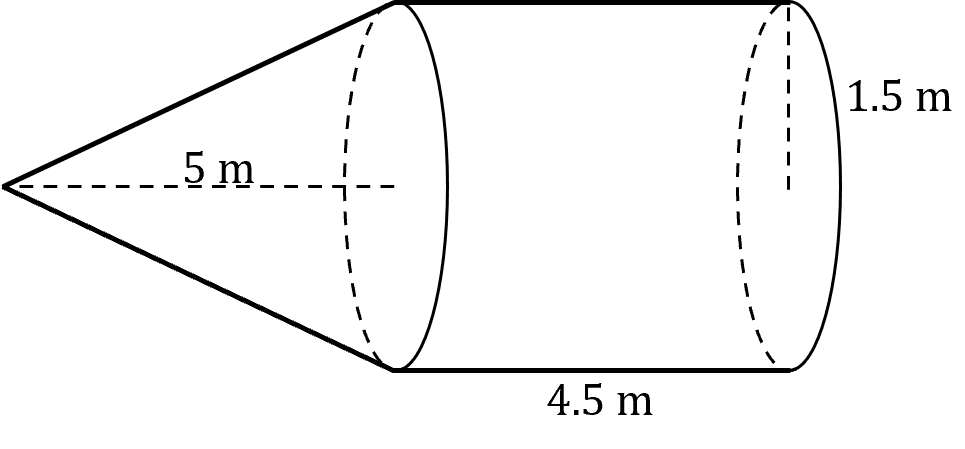
[5 marks]
The surface area of a curved face of a cone is \pi r l, for our cone, the length is 5 \text{ m} and the radius is 1.5\text{ m}, so
\text{Area of the cone face} = 1.5 \times 5 \pi = 7.5 \pi \text{ m}^2
The surface area of a cylinders curved face is pl, the length is 4.5 \text{ m}, but we must find the perimeter
The perimeter is the circumference of the circular base, circumference is 2\pi r, and the radius is 1.5 \text{ m}. So
p= 1 \times 1.5 \pi = 3\pi \text{ m}
The area of the cylinder face the is
\text{Area of cylinder face} = 3\pi \times 4.5 = 13.5 \pi \text{ m}^2
The area of the circular base is
\text{Base area} = \pi \times 1.5^2 = 2.25 \pi \text{ m}^2
So the total surface area is
\text{Surface Area} = 7.5 \pi + 13.5 \pi + 2.25 \pi = 23.25 \pi \text{ m}^2





