Solving Cubic Equations
Solving Cubic Equations Revision
Solving Cubic Equations
Solving higher order equations such as cubics can pose many challenges, the normal way of dealing with these is via trial and improvement.
Trial and Improvement Process
Trial and improvement is the process of taking an educated guess, seeing what result you get, and then improving on your previous guess with a new one.
Example: The solution to the equation x^3-6x=72 lies between 4 and 5. Use trial and improvement to find a solution correct to one decimal place.
Step 1: Make an educated guess, here choose x=4.5 since this is the middle of our range. This the first “trial”.
Step 2: Substitute the trial into the equation
(4.5)^3-6(4.5)=64.125
Step 3: Improve on the previous trial, here choose x=4.6 since the last result was too small.
(4.6)^3-6(4.6)=69.736
This result was too small.
Step 4: Repeat step 3 until you get the opposite outcome, in this case look for a result that is too big. The table shows the various trials and conclusions from each trial.
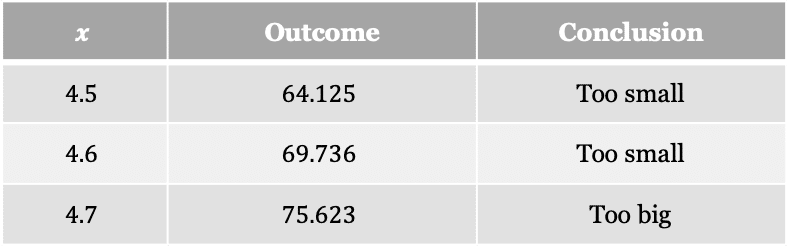
Step 5: Decide which solution to use. Since 4.6 was too small and 4.7 was too big, we must test 4.65 as this is halfway in between.
(4.65)^3-6(4.65)=72.644625
Since this is too big, we must choose x=4.6 as the solution.
Solving Cubic Equations Example Questions
Question 1: The solution to the equation 2x^3+7x=7 lies between 0 and 1. Use trial and improvement to find a solution correct to one decimal place.
[3 marks]
Start at 0.5 since this is the middle of the range.
Create a table of results
| x | Outcome | Conclusion |
| 0.5 | 3.75 | Too small |
| 0.6 | 4.632 | Too small |
| 0.7 | 5.586 | Too small |
| 0.8 | 6.624 | Too small |
| 0.9 | 7.758 | Too big |
Since 0.8 is too small and 0.9 is too big, we must trial 0.85
2(0.85)^3+7(0.85)=7.17825Since this is too big, we choose x=0.8 as the solution.
Question 2: The solution to the equation x^3-11x+15=0 lies between -3 and -4. Use trial and improvement to find a solution correct to one decimal place.
[3 marks]
Start at -3.5 since this is the middle of the range.
Create a table of results
| x | Outcome | Conclusion |
| -3.5 | 10.625 | Too big |
| -3.6 | 7.944 | Too big |
| -3.7 | 5.047 | Too big |
| -3.8 | 1.928 | Too big |
| -3.9 | -1.419 | Too small |
Since -3.9 is too small and -3.8 is too big, we must trial -3.85
(-3.85)^3+11(-3.85)+15=0.283375Since this is too big, we choose x=-3.9 as the solution.
Question 3: The equation 3x^3+x^2-13x+6=0 has a solution between 1 and 2. Use trial and improvement to find a solution correct to one decimal place.
[3 marks]
Start at 1.5 since this is the middle of the range.
Create a table of results
| x | Outcome | Conclusion |
| 1.5 | -1.125 | Too small |
| 1.6 | 0.048 | Too big |
Since 1.5 is too small and 1.6 is too big, we must trial 1.55
3(1.55)^3+(1.55)^2-12(1.55)+6=-0.575875Since this is too small, we choose x=1.6 as the solution.
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.