Nets of 3D Shapes Worksheets, Questions and Revision

Nets of 3D Shapes

Nets of 3D shapes are what the shape would look like if it was opened and laid out flat. You may need to identify or draw nets of different 3D shapes.

Nets Introduction

The net of a 3D shape can be folded into the 3D shape.

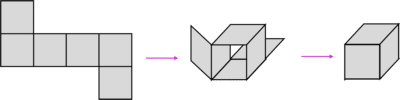
For example, this is a net of a cube:

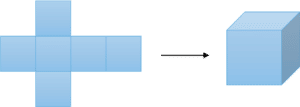
The net above can be folded to create the cube, as follows:

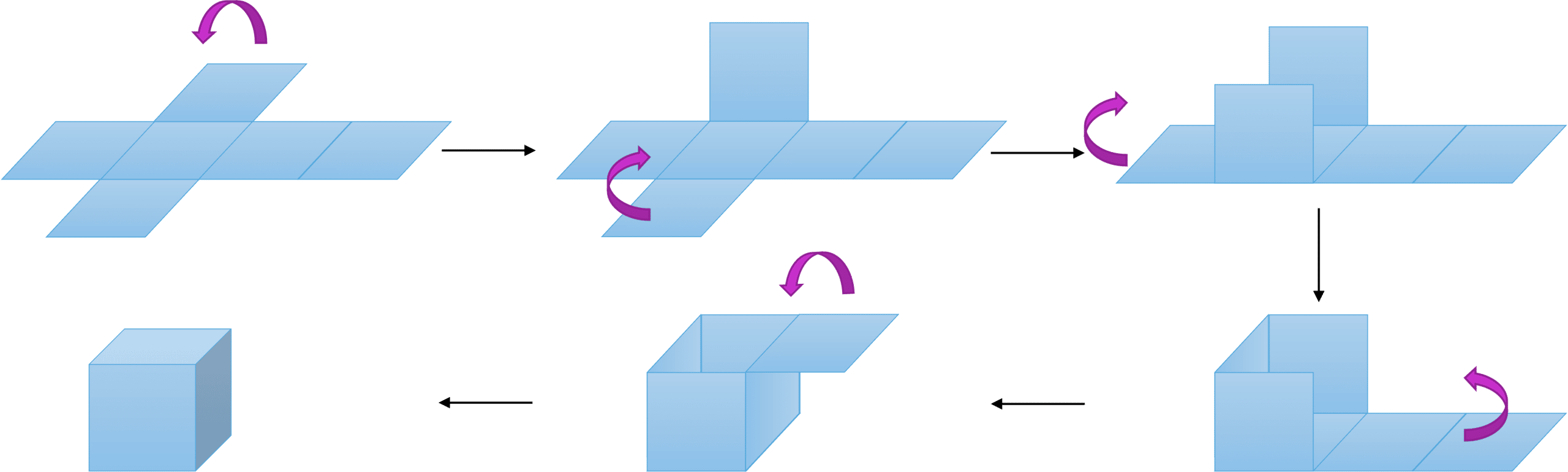
Nets Overview

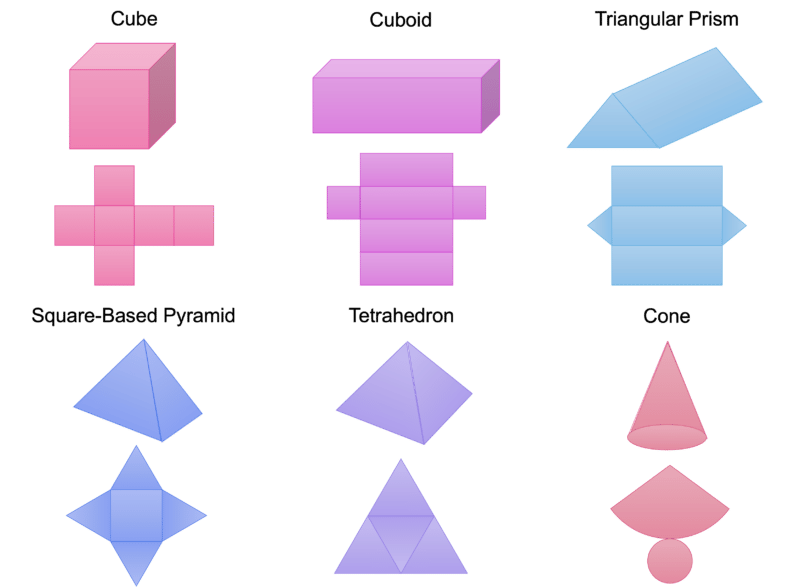
Below are examples of some nets of some 3D shapes. It is important to note, however, that some of the shapes may have more than one possible net (for example, a cube has $11$ ways of formatting a net, all consisting of $6$ squares in a different arrangement.)

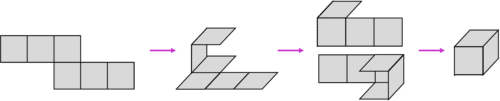
Example 1: Identifying Nets

Identify which of the following are nets of a cube.

[4 marks]

Let’s go through each net and visualise or draw whether this could fold into a 3D cube.

We’ll start with a)

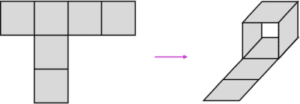
This cannot be folded into a cube as there would be no back to the cube.

Now for b)

This can be made into a cube.

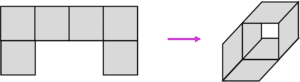
c)

This can also be made into a cube.

And finally, d)

This cannot be folded into a cube as there would be no back for the cube.

Therefore, b and c are nets of a cube.

Example 2: Drawing a Net

Draw the net of a cylinder.

[3 marks]

To draw a net, start by considering which faces the shape has:

A cylinder has two circular faces and one curved rectangular face.

Then consider the faces’ arrangement:

The circles are at either side of the rectangle.

And finally, draw the net:

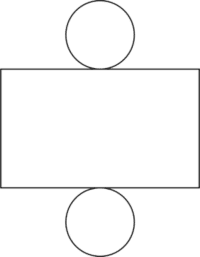
Nets of 3D Shapes Example Questions

Question 1: Draw the net of a following cuboid, including measurements in your net.

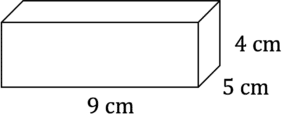
[2 marks]

The net will look like this:

Save your answers with

Gold Standard Education

Sign Up Now

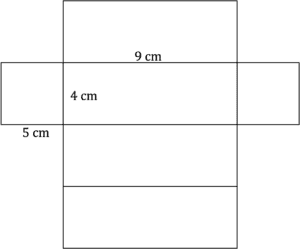
Question 2: Which of the following options is a net for a square-based pyramid?

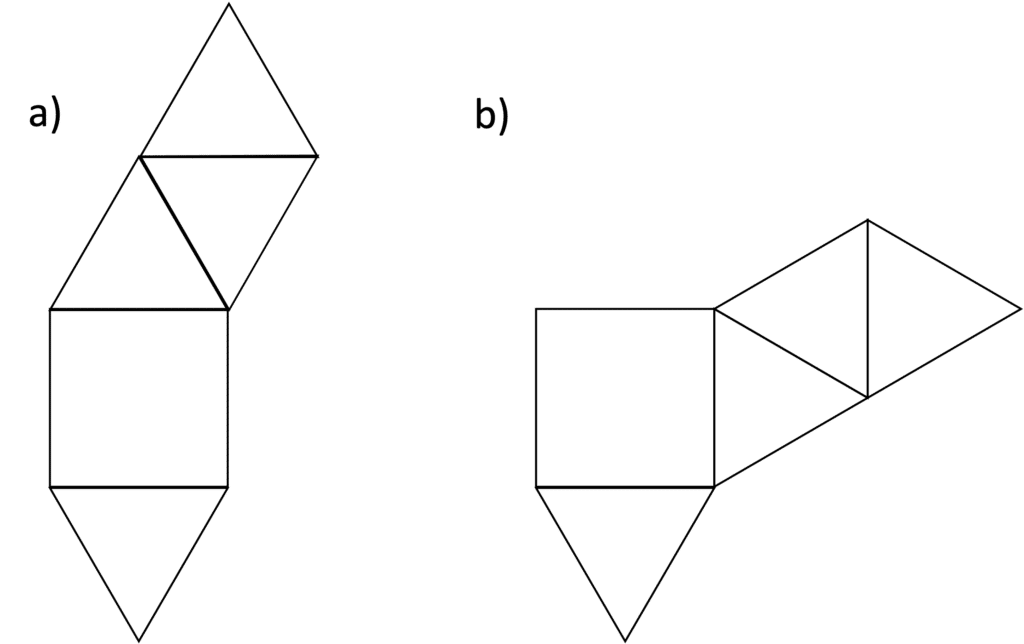
[2 marks]

b) is the only option that can be correctly folded into a square-based pyramid.

Save your answers with

Gold Standard Education

Sign Up Now

Question 3: A cylinder has a diameter of $8\text{ cm}$ and a length of $12\text{ cm}$ .

Which of the following nets is correct for this cylinder?

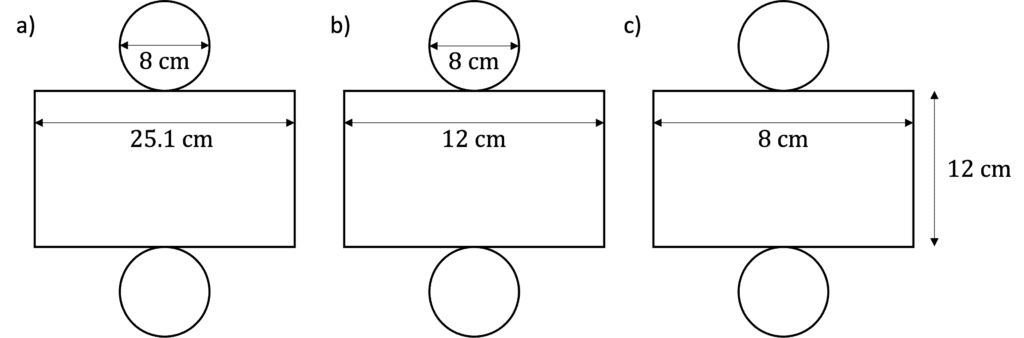
[4 marks]

By looking at the options, we can identify that c) is definitely not correct:

c) cannot be correct as the width of the rectangle should be the same as the circumference of the circle, which is not $8\text{ cm}$ , as this is the diameter, and the circumference is always longer than the diameter.

To work out whether a) and b) is correct, the circumference of the circle needs to be calculated:

Circumference $= \pi d$