Constructions
Constructions Revision
Constructions
Construction is the process of drawing accurate diagrams of shapes, angles and lines. These are called constructions.
It is important to be as accurate as possible, drawing lengths accurate to 2\text{ mm}, and angles accurate to 2\degree. You will need to be able to accurately use a ruler, pair of compasses, and protractor.
Construction 1 – Bisecting a Line
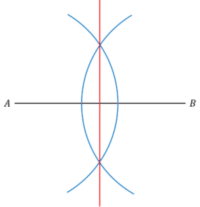
Bisecting means dividing something into two equal parts. So, when bisecting a line, we want to split the line into two lines of equal length.
The bisector of a line will be perpendicular to the original line.
Process:
1. On the line, for example line AB here, start by setting your pair of compasses to a length that is over half the length of AB. For example, if the line was 4\text{ cm}, your compasses would need to be set at over 2\text{ cm}.
Place your pair of compasses at point A and draw an arc crossing the line.

2. Draw another similar arc with your compasses set at point B, keeping your compasses at the same length.
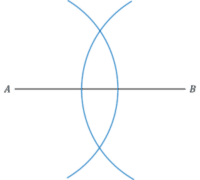
3. Join the two points where the arcs cross with a straight line (drawn with a ruler). This line bisects AB into two equal length lines.
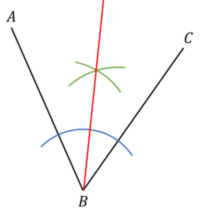
Construction 2 – Bisecting an Angle
When we bisect an angle, we are again trying to split the angle in two equal halves. For example, if an angle was 60\degree, we would bisect it into two angles of 30\degree each.
Bisecting an angle means we are constructing a line equidistant from the two lines forming an angle.
Process:
1. To bisect the angle between the lines AB and BC, start by placing your pair of compasses at B and drawing a small arc that crosses both AB and BC
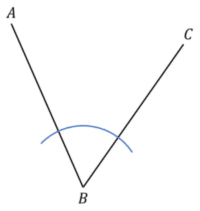
2. Place your pair of compasses at the point where your previous arc crosses the line AB, and draw a small arc between the two straight lines. Repeat this at the crossing point on BC, making sure the arcs cross over.
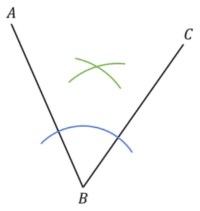
3. Using a ruler, draw a straight line from B, that passes through the point were the middle arcs cross. This is the angle bisector.
Construction 3 – Point to Line
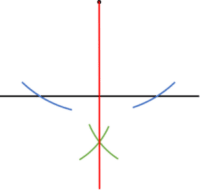
Another construction you may be asked to do is constructing the perpendicular line from a point to a line.
This is where you have a point, and a line, as below, and need to draw a line between them that is perpendicular to the original line.

Process:
1. With your pair of compasses at the point, draw two arcs, at the points where they cross the line.

2. Put your pair of compasses at one of the points whether the arc crosses the line, and draw an arc below the line. Repeat this from the other crossing point, ensuring the new arcs cross over.

3. With a straight line, draw a line from the point that cross the point of intersection between the arcs. This line will be perpendicular to the original line.
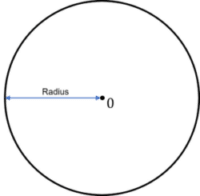
Construction 4 – Circles
You may be required to draw a circle using a pair of compasses.
To do this, set your compasses to the length of the radius of your desired circle, and place it where you would like the centre of the circle to be (0). Draw the full circumference of the circle until your arc reaches the start of your arc.
Make sure to draw lightly to avoid the pair of compasses moving.
Construction 5 – Triangles
You may be asked to construct some triangles when given at least 3 pieces of information about the triangle.
You will need one of the following options of information:
- Side Angle Side (SAS)
- Angle Side Angle (ASA)
- Side Side Side (SSS)
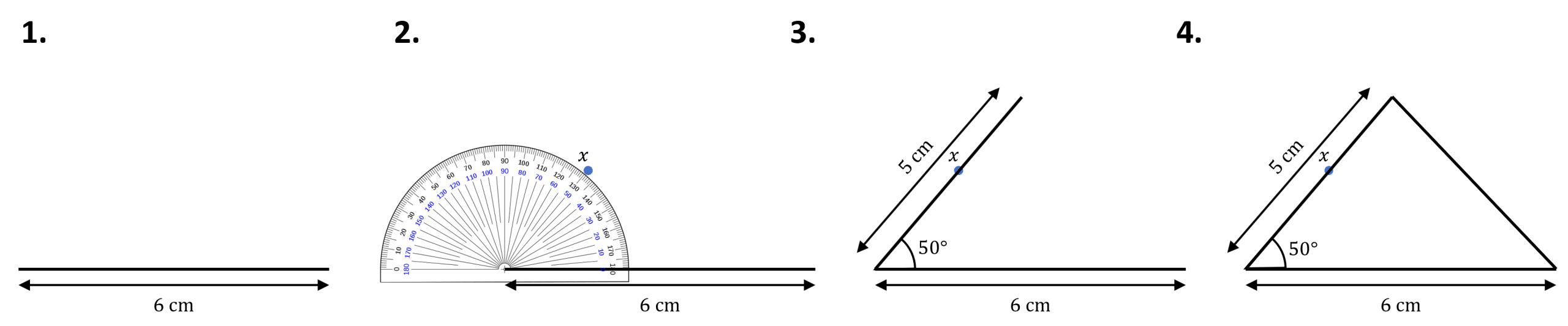
Process – SAS
Example – construct a triangle with two sides of lengths 5\text{ cm} and 6\text{ cm}, with an angle of 50\degree between them.
1. With a ruler, draw the longest side
2. Using a protractor, measure the angle 50\degree and draw a dot to show this angle (x)
3. Draw a line of 5\text{cm} crossing, reaching, or going through, the point x (depending on how far the point x is), but extending your ruler through x to ensure the angle is correct.
4. Finally, join up these two lines with a third line. This is the final triangle.
Process – ASA
Example – construct a triangle with two angles 40\degree and 65\degree, with a side of length 7\text{ cm} between them.
1. With a ruler, draw the side
2. Using a protractor, measure the angle 40\degree from one side of the line and draw a dot to show this angle (x)
3. Draw a long line through x
4. From the other side of the line, use a protractor to measure 65\degree, and draw a dot showing this angle (y)
5. Draw a line through y, to the point it reaches the other line.

Process – SSS
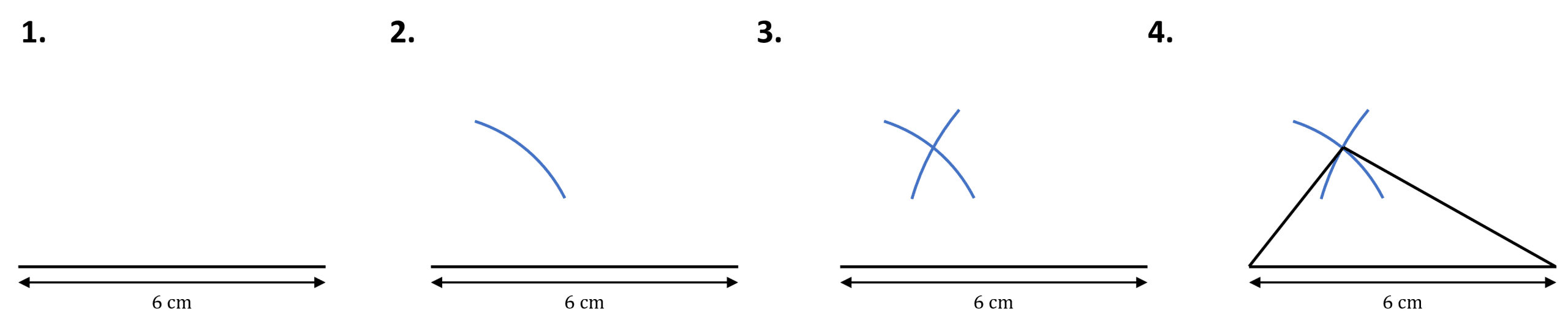
Example – construct a triangle with sides of lengths 6\text{ cm}, 3\text{ cm}, and 5\text{ cm}.
1. With a ruler, draw the longest side, 6\text{ cm}
2. Set your pair of compasses to one of the other lengths, for example 3\text{ cm} and draw an arc from one of the ends of the 6\text{ cm} line.
3. Repeat with your pair of compasses at 5\text{ cm}, with centre at the other side of the 6\text{ cm} line.
4. Draw lines from either end of the 6\text{ cm} line, joining at the point of intersection between the two arcs.
Construction 6 – Quadrilaterals
To construct quadrilaterals, we split them into 2 triangles, and use the methods we learnt for constructing triangles to construct the quadrilateral.
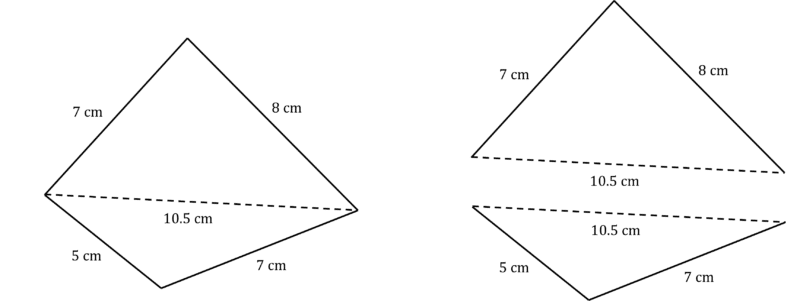
To construct a quadrilateral, you need 5 pieces of information. For example, side lengths, angle sizes, or the length of the diagonal through the quadrilateral.
For example, you might be asked to construct a quadrilateral with sides of lengths AB=7\text{ cm}, BC=8\text{ cm}, CD=7\text{ cm}, and DA=5\text{ cm}, with a diagonal length AC=10.5\text{cm}.
This can be split into two triangles, and then the triangles can be drawn using the SSS method described earlier:
Construction 7 – Angles
You will also need to know how to construct angles of 60\degree, 30\degree, 90\degree, and 45\degree
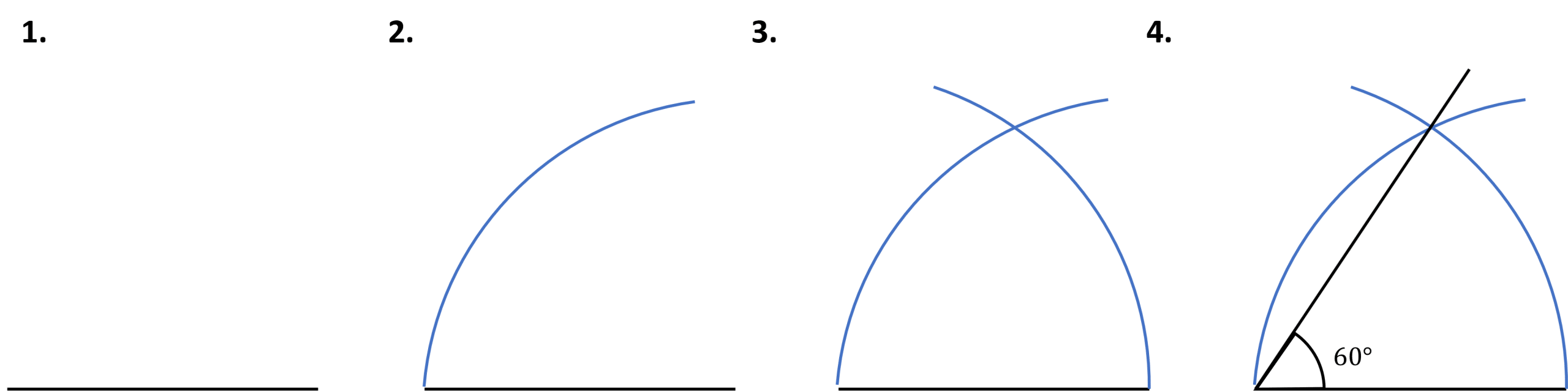
Process – 60\degree
1. Draw a line of any length.
2. Set your pair of compasses to the same length as the line as draw a curve from one end.
3. Repeat from the other end.
4. Draw a line to where the arcs intersect – this forms a 60\degree angle.
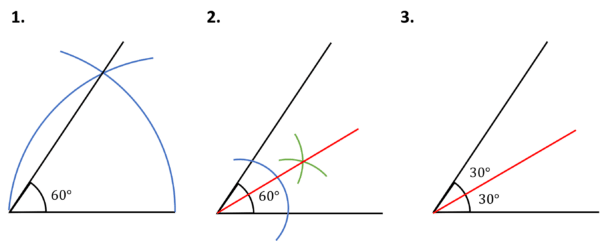
Process – 30\degree
1. Construct a 60\degree angle as above.
2. Bisect this 60\degree angle.
3. This creates two angles of 30\degree.
Process – 90\degree
1. Draw a straight line and bisect it.
2. This creates 2 angles of 90\degree
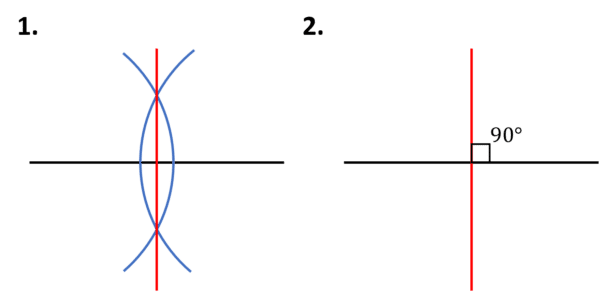
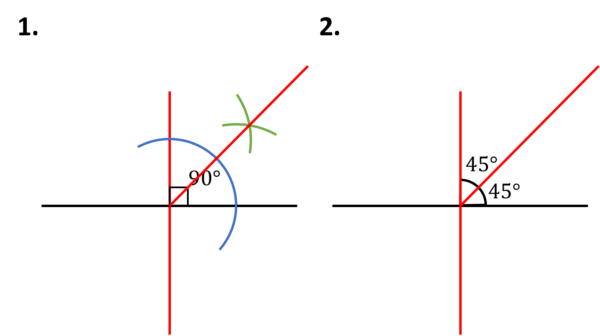
Process – 45\degree
1. Construct a 90\degree angle as above, and bisect this angle.
2. This creates 2 angles of 45\degree
Constructions Example Questions
Question 1: Would it be possible to construct a triangle given 3 angles?
[1 mark]
No, as the triangle could be any size and have the 3 given angles.
Question 2: Which option is the correct first step to bisect an angle?
a) 
b) 
c) 
d) 
[2 marks]
d is the correct first step.
Question 3: Select the option that correctly shows the first 2 steps of drawing a triangle with the following length sides:
AB: 5\text{ cm}\\ AC: 2\text{cm}\\ BC: 4\text{ cm}
a) 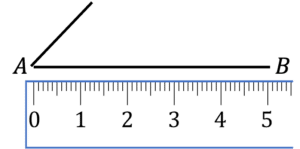
b) 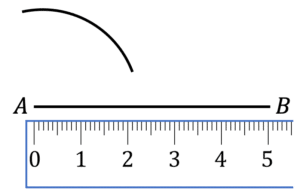
c) 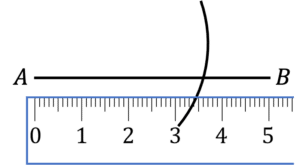
d) 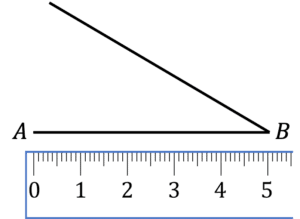
[2 marks]
b is the correct first steps.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.