Circle Arcs, Sectors and Segments
Circle Arcs, Sectors and Segments Revision
Circle Arcs, Sectors and Segments
A circle can be split into arcs, segments and sectors.
You will need to be able to find arc lengths, segment area and perimeter, and sector area and perimeter.
Introduction
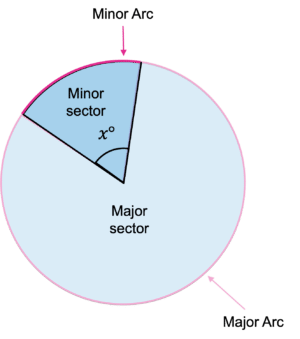
It is important to be able to recognise the parts of a circle, and whether each section is minor and major.
For sectors, the minor sector is the always the sector that has an angle, (x\degree) at the centre smaller than 180\degree, and the remainder of the circle is the major sector.
The minor sector produces the minor arc, as follows:
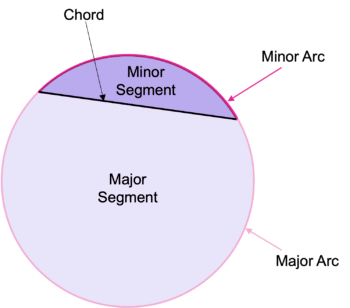
For segments, the segment that is smaller than half of the area of the circle is the minor segment, enclosed by a chord and the minor arc, and the remainder of the circle is the major segment, as follows:

Arc Length
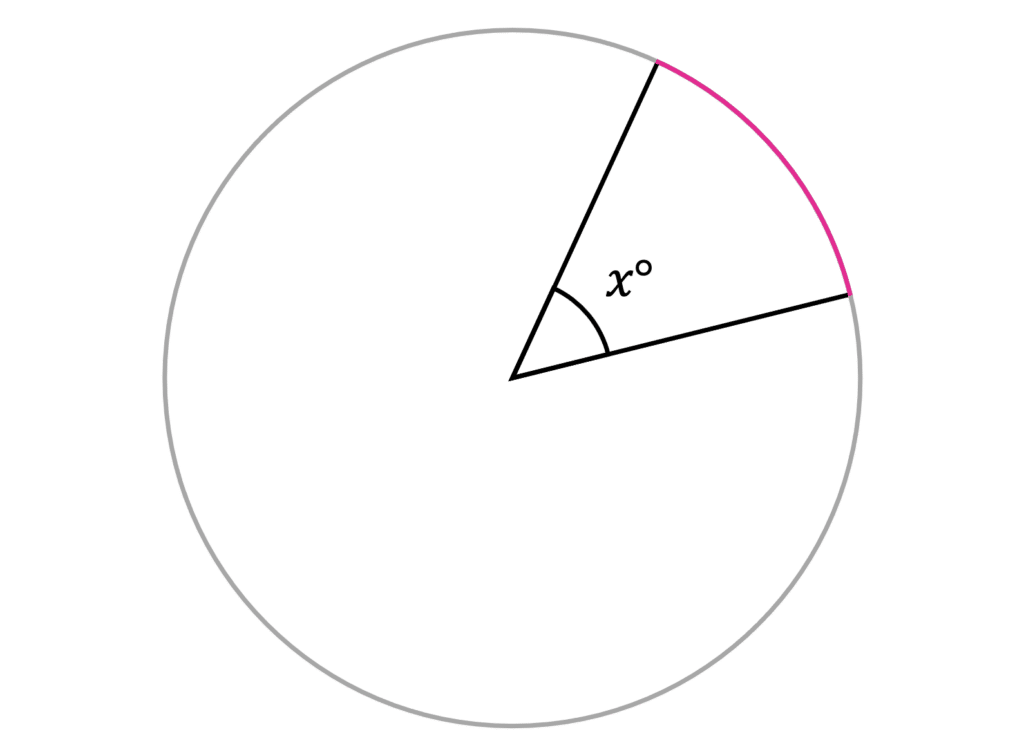
To calculate arc length, you will always need to size of the angle at the centre of the sector, and the circumference of the full circle.
Arc length can be calculated using the following equation:
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle


Sector
Area
To calculate the area of a sector, you will again need the angle in the centre, as well as the area of the full circle.
Sector area can be calculated using the following equation:
Area of Sector = \dfrac{x}{360}\times Area of full Circle


Perimeter
To find the perimeter of a sector, you add together the arc length and the two radii that outline the sector, or:
Perimeter of a Sector = Arc Length + 2r
Where r is the radius.
Segment
A segment can be considered the “end” of a sector.
This means, we can use the angle at the centre to help us work out perimeter and area.

Perimeter
To calculate the perimeter of a segment, you need to add the arc length and the length of the chord:
Perimeter of a segment = arc length + chord length
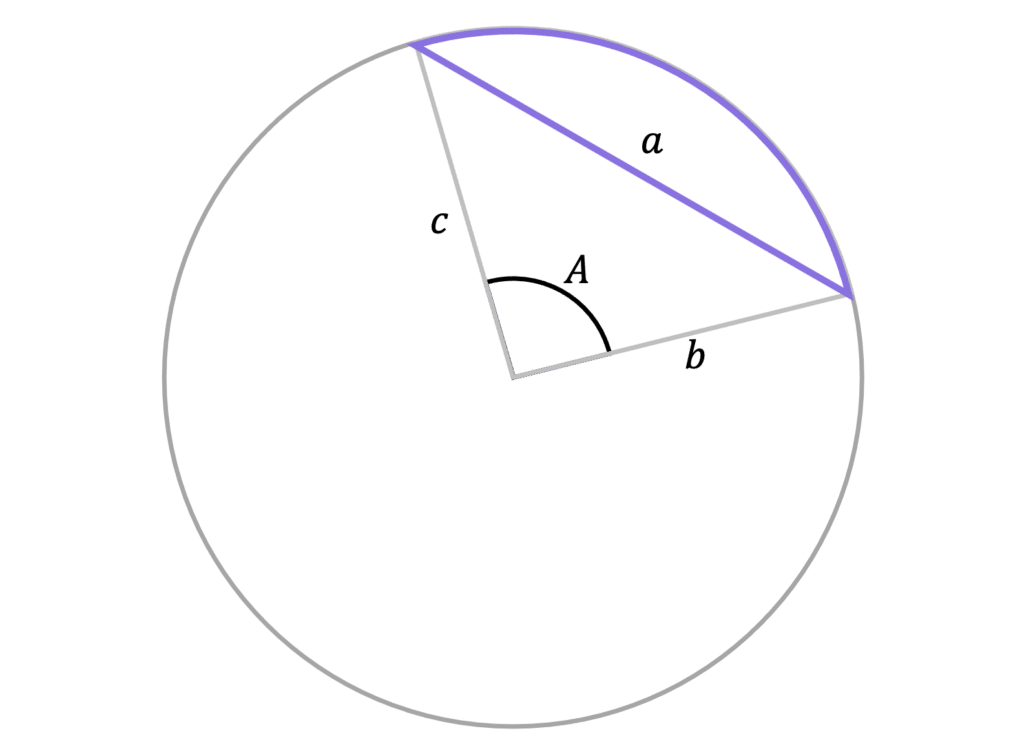
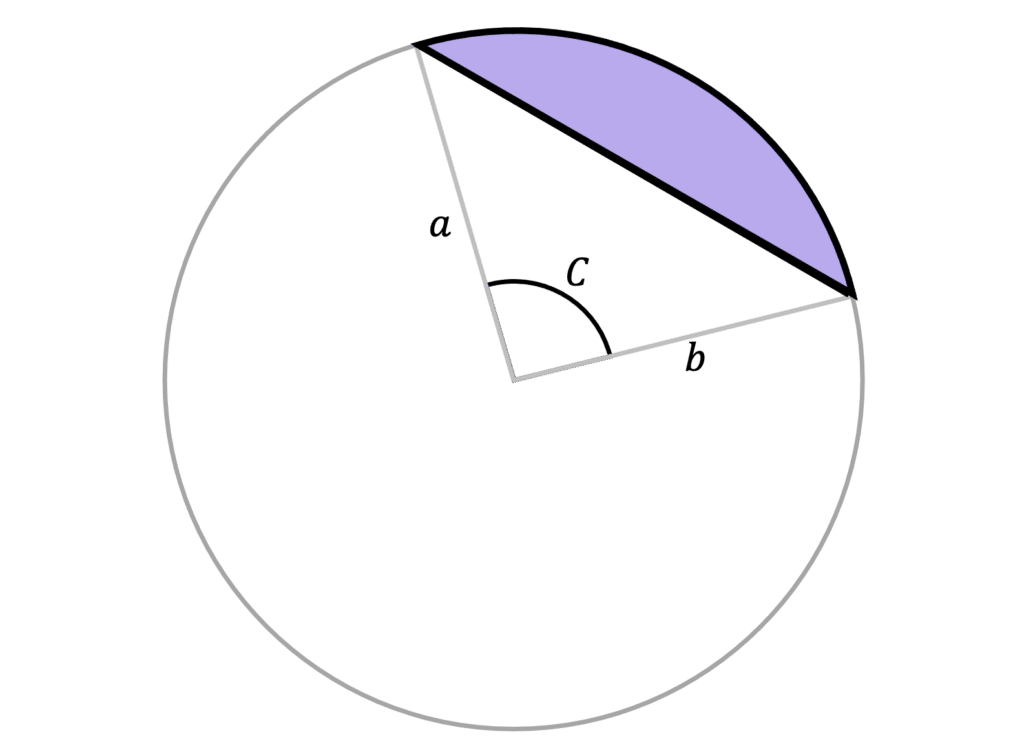
We may also need to work out the chord length if this is not given. We can do this by using the angle size and the length of the radii to use the Cosine rule:
a^2=b^2+c^2-2bc\cos(A)
Where b and c are radii.
As b and c are radii, they are equal to each other, and the equation can be simplified to,
a^2=2b^2-2b^2\cos(A)
Where b is the radius.

Area
To calculate the area of a segment, you need to find the area of the full sector, and subtract the area of the triangle next to the segment, or:
Area of segment = Area of sector - Area of triangle
The area of the triangle can be calculated using:
Area of triangle = \dfrac{1}{2} ab\sin(C)
Which can be simplified to,
Area of triangle = \dfrac{1}{2} a^2\sin(C)
Where a is the radius.
Example 1: Sector Perimeter and Area
Find the perimeter and area of the following sector, which is part of a circle with radius 5\text{ cm}
Give your answers to the nearest whole number.
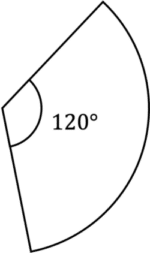
[4 marks]
Area:
We will use the equation,
Area of Sector = \dfrac{x}{360}\times Area of full Circle
The area of the full circle is,
\pi r^2 = 25\pi
So the area of the sector is,
\dfrac{120}{360}\times25\pi = 26\text{ cm}^2
Perimeter:
We need to find the arc length to find the perimeter, using:
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
The circumference of the full circle is,
2\pi r = 10\pi
Therefore, the arc length is,
\dfrac{120}{360}\times10\pi=10\text{ cm}
And the perimeter is,
10 + 5 + 5 = 20\text{ cm}
Example 2: Segment Area
Calculate the area of the shaded area to 2 decimal places:
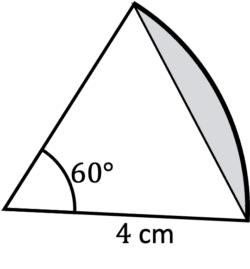
[4 marks]
The shaded area is a segment, so we can use the equation:
Area of segment = Area of sector - Area of triangle
So first, we need to calculate the area of the sector,
Area of full circle:
\pi r^2 = 16\pi
Area of sector:
\dfrac{60}{360}\times16\pi=\dfrac{8}{3}\pi
And now the area of the triangle,
\dfrac{1}{2} ab \sin(C) = \dfrac{1}{2}\times4\times4\times\sin(60) = 4\sqrt{3}
Finally, we can calculate the area of the segment:
Area of segment = Area of sector - Area of triangle
Area of segment =\dfrac{8}{3}\pi - 4\sqrt{3} = 1.45\text{ cm}
Circle Arcs, Sectors and Segments Example Questions
Question 1: Calculate the length of the arc subtended from a sector with radius 12\text{ cm}, and an angle 40\degree to 1 decimal place.
[3 marks]
Using the equation,
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
Firstly, we need to work out circumference of full circle,
2\pi r = 24\piAnd then the arc length,
\dfrac{40}{360}\times24\pi=8.4\text{ cm}Question 2: Work out the area of the major sector in this diagram, to the nearest whole number:
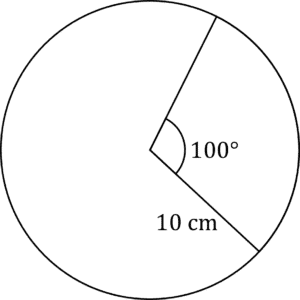
[4 marks]
The questions asks for the area of the major sector, so we are doing the larger sector on the circle, this means the angle in the centre is,
360-100=260\degreeWe need to find the full area of the circle first,
\pi r^2 = 100\piAnd now we can work out the area of the major sector,
\dfrac{260}{360}\times 100\pi = 227\text{ cm}^2Question 3: Calculate the perimeter of the shaded segment, to 1 decimal place.
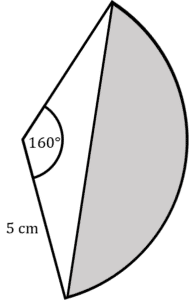
[4 marks]
To find the perimeter of a segment, we need arc length and chord length.
First, we will work out arc length,
Circumference of circle:
2\pi r = 10\piArc length:
\dfrac{160}{360}\times 10\pi = \dfrac{40}{9}\pi
Now, to work out chord length we will use,
a = \sqrt{b^2+c^2-2bc\cos(A)}\\ \sqrt{5^2+5^2-2(5)(5)\cos(160)}=9.848...\text{cm}
Perimeter:
\dfrac{40}{9}\pi + 9.848... = 23.8\text{ cm}






