Scale Drawings
Scale Drawings Revision
Scale Drawings
A scale drawing portrays a real object with the lengths in proportion to the lengths of the actual object, but reduced or enlarged by a scale factor.
You may be asked to find the scale (or scale factor), and/or calculate actual distances based on a scale drawing.
Scales and Scale Factors
Below is a scale drawing of a tennis court with a scale 1\text{ cm}:4\text{ m} or 1:400.
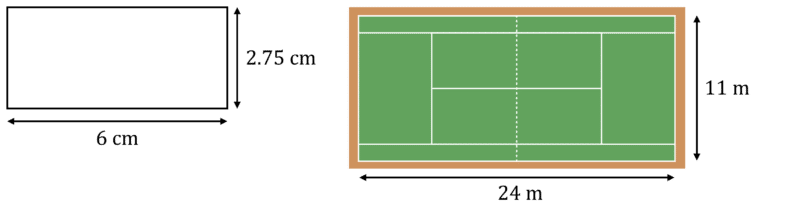
We can use a scale of 1:400 to calculate the scale factor, by dividing the left hand side of the ratio by the right hand side:
Scale factor: 1\div400=\dfrac{1}{400}
This means, the actual tennis court size has been enlarged by a scale factor of \dfrac{1}{400} to give the scale drawing.
If we did not have the scale, we could work out both the scale and the scale factor from the drawing:
Scale: we can use any length from the scale drawing and actual object to calculate this, making sure to choose the equivalent side in both.
Length scale drawing : Length actual object
6\text{ cm}:24\text{ m}\\ 6\text{ cm}:2400\text{ cm}\\ 1\text{ cm}: 400\text{ cm}\\ 1:400
Scale factor: again, choose equivalent lengths from the scale drawing and actual image.
Length scale drawing \div Length actual drawing
6\div2400\\ 1\div400\\ \dfrac{1}{400}
Calculating Lengths
We can use a scale or scale factor to calculate lengths or distances when given only a scale drawing.
Here is a scale drawing of a rug with scale 1:15, calculate the length and width of the actual rug.
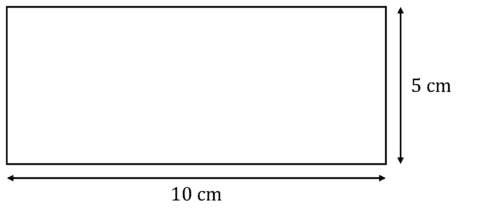
Length: the length of the scale drawing is 10\text{ cm} and the scale is 1:15.
The 1 in this ratio represents the scale drawing, and the 15 represents the actual rug, so the actual rug is 15 times the size of the scale drawing.
Therefore, the length is 10\times15=150\text{ cm}
Width: we can do the same here but using the value of the scale drawing’s width: 5\text{ cm}.
Therefore, the width is 5\times15=75\text{ cm}
Note: if we were told instead that the scale factor of the actual rug to the image is \dfrac{1}{15} here, to find the length we would:
10\div\dfrac{1}{15}=150\text{ cm}
Drawing Scale Diagrams
You may be asked to draw a scale drawing based off actual dimensions.
For example:
Below is an image of a rectangular door showing its actual dimensions. Given that the scale is 1:8, draw a scale drawing of the door.

To draw a scale drawing, you firstly need to work out the length of the sides of the drawing using the method we learnt previously:
As we have the actual object’s size, we will divide the width and height by 8 to find the scaled lengths:
Width: 80\div8=10\text{ cm}
Height: 200\div8=25\text{ cm}
Therefore, we need to draw a rectangle with width 10\text{ cm}, and height 25\text{ cm}:
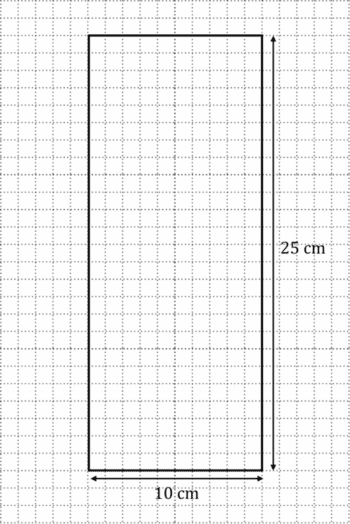
Where the squares in the paper are 1\text{ cm}
Example 1: Scales and Scale Factors
Below is a scale drawing of a box in comparison to the actual box. Calculate the scale of this drawing.
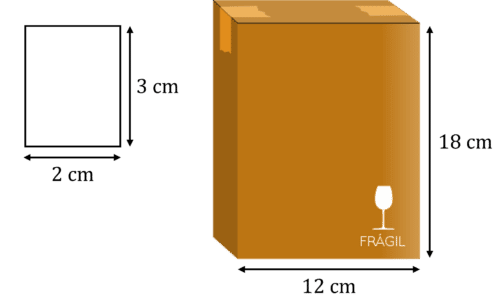
[2 marks]
To calculate the scale, we need to find a ratio:
Length scale drawing : Length actual object
2\text{ cm}:12\text{ cm}\\ 1:6Note: we could have used the heights of this boxes to calculate this and it would have given the same answer.
Example 2: Calculating Lengths
Below is a scale drawing of a ball. The actual ball has been enlarged by scale factor \dfrac{1}{9}. Calculate the diameter of the actual ball.
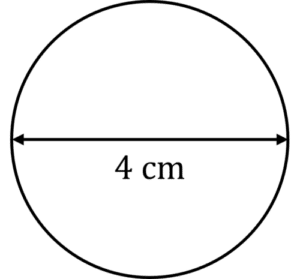
[2 marks]
To calculate the diameter, we need to divide the scale drawing’s diameter by the scale factor:
4\div\dfrac{1}{9}=36\text{cm}
Scale Drawings Example Questions
Question 1: The following scale drawing represents an ice cream cone scaled by 1:5. Calculate the height of the actual ice cream cone.
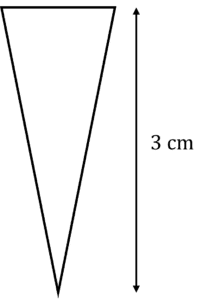
[2 marks]
The scaled height is 3\text{ cm} and the scale is 1:5, so we multiply 3 by 5 to find the actual height:
3\times5=15\text{ cm}Question 2: A scale drawing of a bus has length 12\text{ cm}, while the actual bus’ length is 12\text{ m}, find the scale in its simplest form.
[2 marks]
The ratio of scaled to actual is:
12\text{ cm}:12\text{ m}Convert meters to centimeters:
12\text{ cm}:1200\text{ cm}We can then divide this by 12 to find the simplest form:
1:100Question 3: A map has scale 1:120000. The distance between Jemima’s house and school on the map is 8\text{ cm}. Find the actual distance between Jemima’s house and school, giving your answer in \text{km}.
[3 marks]
Firstly, multiply the scaled distance by the ratio:
8\times120000=960000\text{ cm}To convert \text{cm} to \text{km}, we divide by 100000:
960000\div100000=9.6\text{km}




