Growth and Decay
Growth and Decay Revision
Growth and Decay
There are two types of interest we shall look at
- Simple interest, where the interested is calculated against the initial investment
- Compound interest, where the interest calculated on the initial investment and the interest already earned. As you earn interest on the interest, it compounds.
We shall also look at depreciation, where the value decreases by a percentage of itself.
Simple Interest
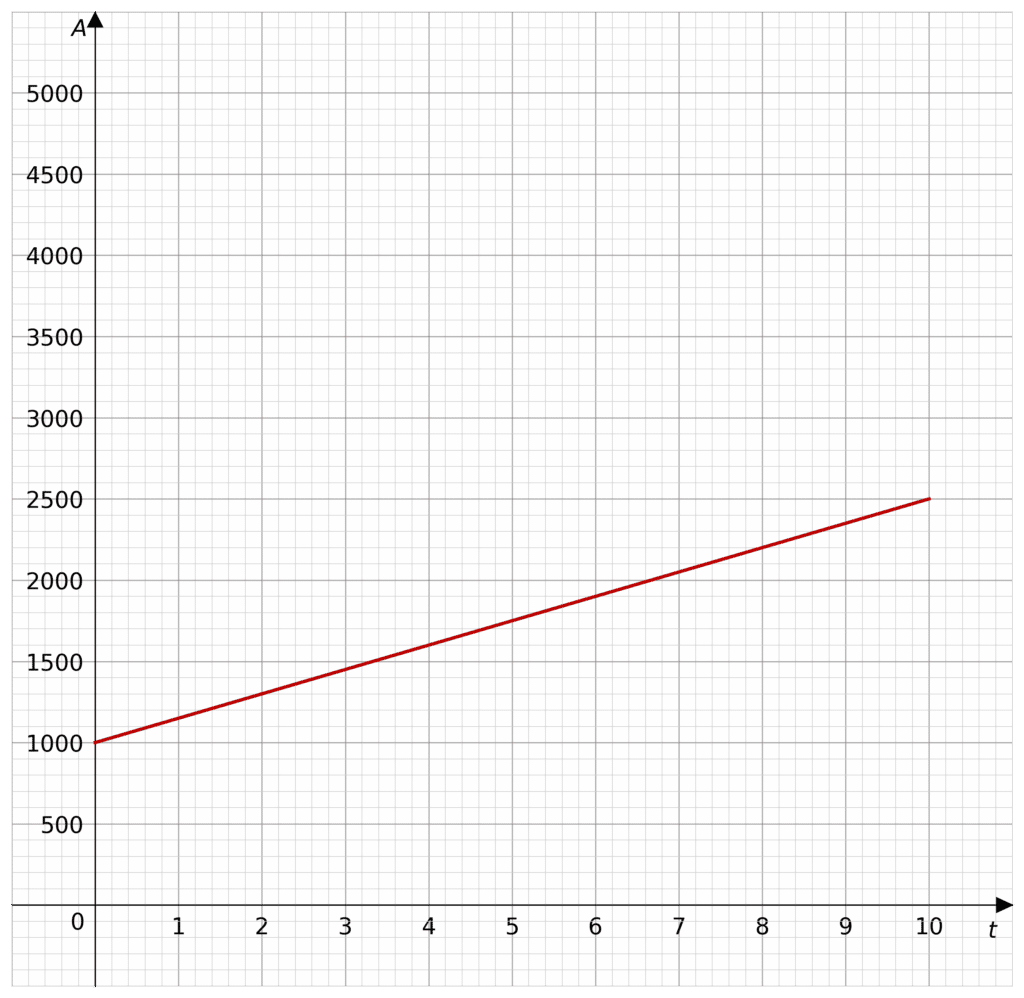

Simple interest takes an initial investment, sometimes called the principal investment, P, and increases it by an interest rate, r, every increment of time, t. This increment of time is usually per year, but could be per month, or per quarter. So t is the time in years for our sake.
Remember if the interest rate is 5\% then 5\% of P is
0.05 \times P
So to increase by 5\%
P+0.05P
So the value of r=0.05, and if we want to increase by 5\% of P every year then
P+rPt
where t is the number of years. So the formula for simple interest is
A= P+rPt
or
A=P(1+rt)
where A is the final amount. Remember r is as a decimal, not a percentage.
The example picture is when P=1000 and the interest rate is 15\% under simple interest.
Year-on-Year Compound Interest
Sometimes the interest rate (or depreciation rate) does not stay the same year-on-year. For example, if a classic car is worth £20,000 when it is bought by a collector, then if it appreciates in value, the rate may change year upon year. If the rate of appreciation is 10\%, 20\% and 15\% after 1, 2 and 3 years respectively, then we can calculate the value of the car after each year.
One year after purchasing the car, it will have a value of
£20,000 \times (1+0.1) = £22,000
after two years,
£22,000 \times (1+0.2) = £26,400
and after three years,
£26,400 \times (1+0.15) = £30,360
We can observe that unlike in simple interest, the value appreciates on how much the car was worth at the end of the previous year, not by how much it was worth at the start. This is why we call this compound interest, because the amount of interest received each year is not fixed like in simple interest, but may compound on itself, earning interest on the interest.
Compound Interest
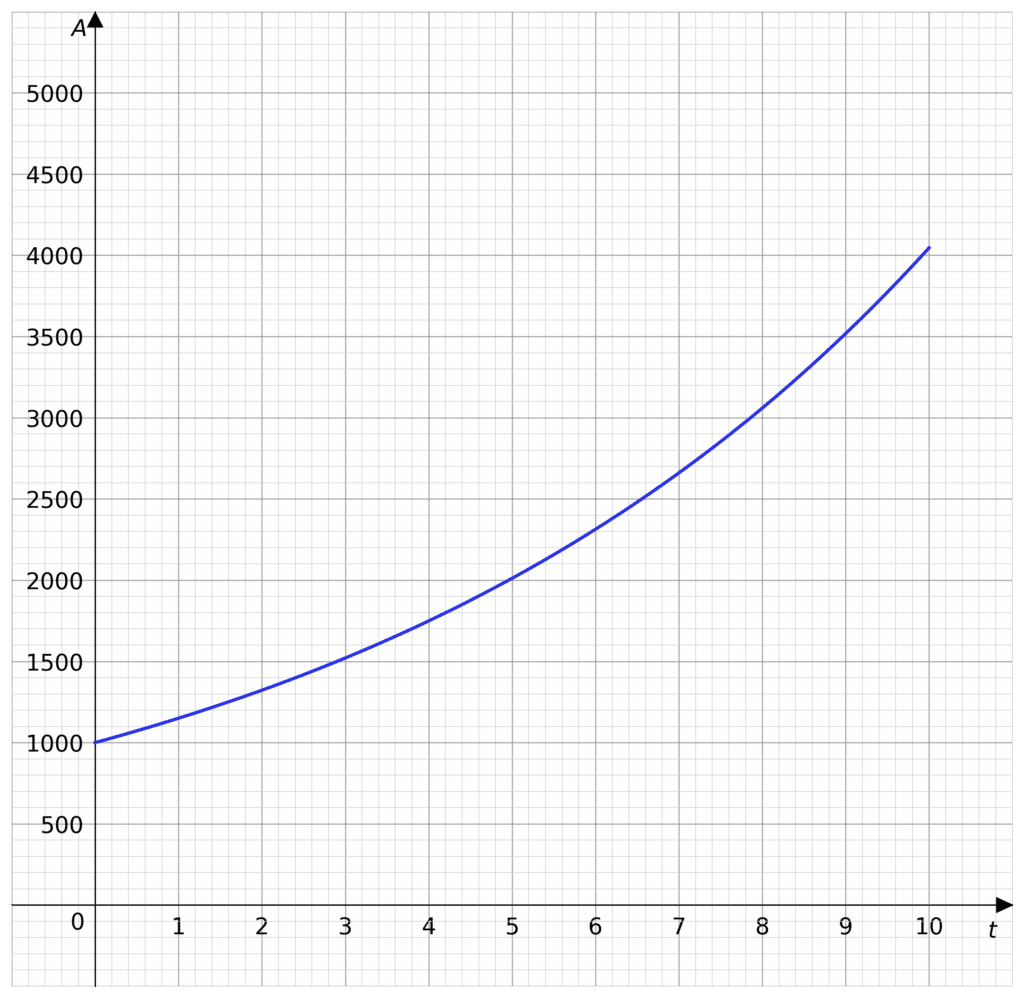

Compound interest takes the principal investment, P and increases it by the interest rate, r. Then, the next time the interest is added, the interest is calculated on the principal investment and the added interest.
So, let’s say the interest rate is 5\% again so r=0.05, added once a year. Then you end the first year with
P(1+0.05) = 1.05P
Now for the second year, you calculate the added interest form 1.05P, instead of P. So for year 2 we find 5% of 1.05P
1.05P\times(1+0.05)= P \times (1.05)^2
Recalling 1.05 = 1+r, then for year two
P\times (1+r)^2
Similarly for year 3
P\times (1+r)^3
So the formula for compound interest, where A is the total amount after t years is
A=P(1+r)^t
The example picture is of when P = 1000 and the interest rate of 15\% under compound interest.
Decay
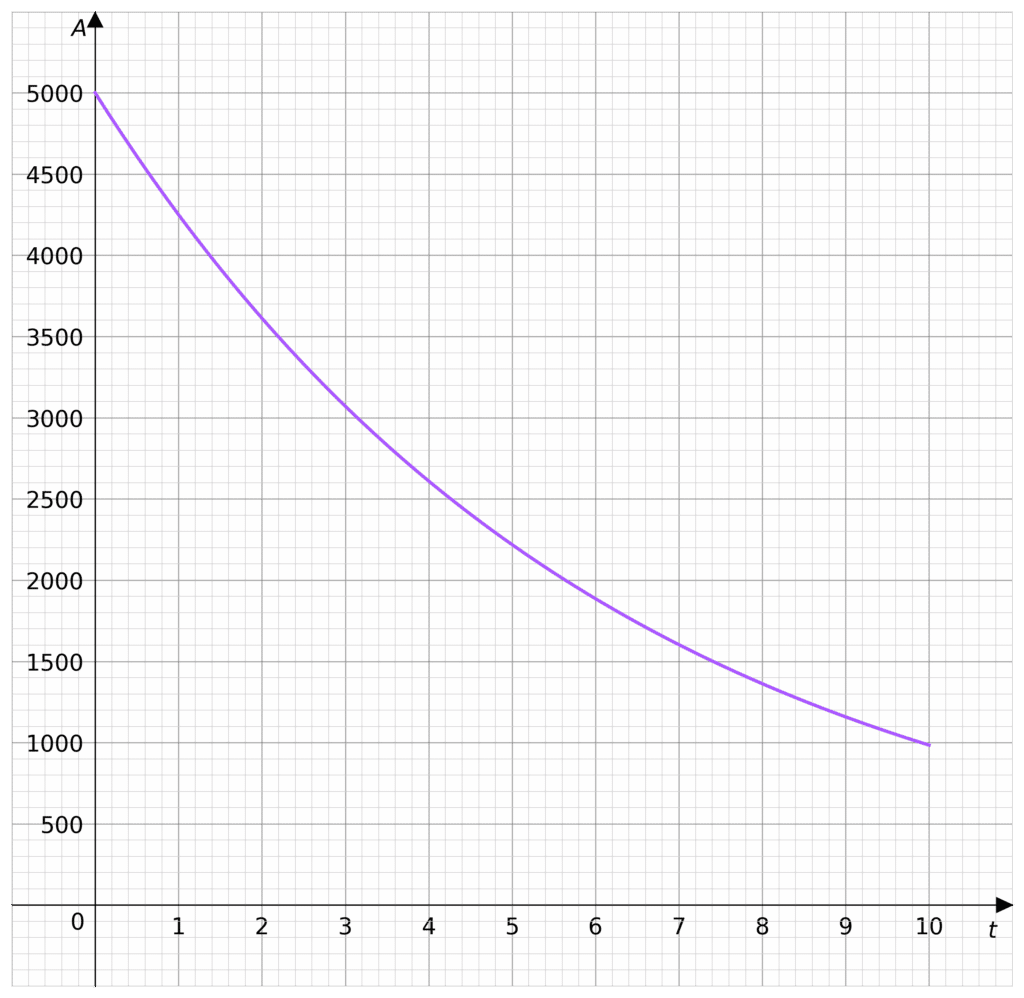

Decay in financial terms is called depreciation. Decay is when an amount is reduced by a percentage of itself every increment of time. Depreciation is when the value of something decays. Similarly to compound interest, depreciation is compounded.
If an asset (like a car or a stock portfolio) has initial value P, and it decreases in value by the depreciation rate of 5\%, then we calculate that by
P\times (1-0.05)
So if it depreciates by depreciation rate r, every year, then let t be the time in years, and A be the final amount.
A=P(1-r)^t
The example picture is when P=5000, and it is depreciating at a rate of 15\%
Example 1: Simple Interest
A loan has simple interest on it. For every month the money is not paid off, 8\% of the amount borrowed is added to the total debt. If £1000 is borrowed, how much is owed after 4 months?
[3 marks]
Firstly we call the amount borrowed P=1000, the interest rate is r=0.08 and t=4, so let the total debt be £A.
Substituting these into the simple interest equation we get
A= P(1+rt)
A=1000 \times (1+0.08 \times 4)
A=1000(1.32)
A=1320
So the total debt is £1320
Example 2: Year-on-Year Compound Interest
A car is purchased new for £25,000.
This car depreciates in value by 20\%, 15\% and 9\% after 1, 2 and 3 years, respectively.
Calculate the value of the car after 3 years.
[3 marks]
First, we must work out the value of the car after 1 year:
\text{Value} = £25,000 \times (1-0.2) = £20,000
After 2 years:
\text{Value} = £20,000 \times (1-0.15) = £17,000
After 3 years:
\text{Value} = £17,000 \times (1-0.09) = £15,470
Hence the value of the car after 3 years shall be £15,470
Example 3: Compound Interest
Ethan invests £156,250 for 3 years at 4\% compound interest.
Work out the value of this investment after 3 years. Give your answer to the nearest pound.
[3 marks]
Firstly we all the amount invested P=156,250, the interest rate is r=0.04 and t=3, so let the total value be £A.
Substituting these into the compound interest equation we get
A=P(1+r)^t
A=156,250 \times (1+0.04)^3
A=156,250(1.04)^3
A=175,760
So the total value after three years is £175,760
Growth and Decay Example Questions
Question 1: Two bank accounts offer simple interest.
Bank 1 offers an interest rate of 4\% per year.
Bank 2 offers an interest rate of 2\% per year, but will give you an additional £200 to add to you initial investment.
Sarah wants to put £4000 in one of these banks for 4 years. Which bank would leave her with the most money after 4 years?
[4 marks]
Bank 1: after four years, P=4000, t=4
A=4000\times(1+0.04\times 4)
A=4000(1.16)
A = £4640
Bank 2: After four years, P=4200, t=4
A=4200\times (1+0.02\times 4)
A=4200(1.08)
A=£4532
So for Sarah, Bank 1 will make her more money.
Question 2: A house is bought for £200,000.
This value of the house appreciates by 8\%, 5\% and 3\% after 1, 2 and 3 years, respectively.
a) How much is the house worth after one year?
[1 mark]
b) By how much has the house’s value increased after 3 years.
[2 marks]
a) The value of the house appreciates by 8% after one year
\text{Value} = £200,000 \times (1+0.08) = £216,000
b) After 2 years:
\text{Value} = £216,000 \times (1+0.05) = £226,800
After 3 years:
\text{Value} = £226,800 \times (1+0.03) = £233,604
After 3 years the house is worth £233,604, so the increase in value is
233,604 - 200,000 = £33,604
Question 3: A fund begins with £12,000 in it, it increases by a compound interest of 10\% per year.
After n years the fund is worth £17569.20
Work out the value of n.
[3 marks]
Let the value of the fund be £A =£12,000, the initial investment be £P=£12,000 and let the interest rate be r=0.1
Substituting into the compound interest formula we get
17,569.2=12,000(1+0.1)^n
17,569.2=12,000(1.1)^n
\dfrac{17,569.2}{12,000} = 1.1^n
1.4641=1.1^n
So now we can raise 1.1 to various powers until we find n
1.1^2=1.21
1.1^3=1.331
1.1^4=1.4641
So n=4
Question 4: The value of a car depreciates by 12\% each year.
a) After how many years will the cars value drop below 60\% for the first time?
[3 marks]
b) If the car was worth £13,500 when new, how much is the car worth after 10 years?
Give your answer to the nearest pound.
[2 marks]
a) If the value new is P and the interest rate is r=0.12, then 60\% of the cars original value is 0.6P, so using the depreciation formula we get
A=P(1-0.12)^t
Where t is the time in years and A is the total value of the car. So when the value drops below 60\% for the first time
P(0.88)^t<0.6P
0.88^t<0.6
So now we can test values of t.
0.88^2=0.7744
0.88^3=0.681472
0.88^4=0.59969536 <0.6
So year 4 will be the year the cars value drops below 60\% for the first time.
b) Using the formula with P=13,500 and t=10 we get
A=13,500(1-0.12)^{10}
A=13,500(0.88)^{10}
A=3759.76317...
So the value of the car after 10 years is £3760 to the nearest pound.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.