Revise
Graph Translations and Reflections
Graph Translations and Reflections Revision
Graph Translations and Reflections
We shall look at two types of graph transformations.
Firstly we shall look at translations, which move the position of the graph up, down, left and right.
Then we shall look at reflections, where the graph is reflected over a line of reflection.
Horizontal Translations
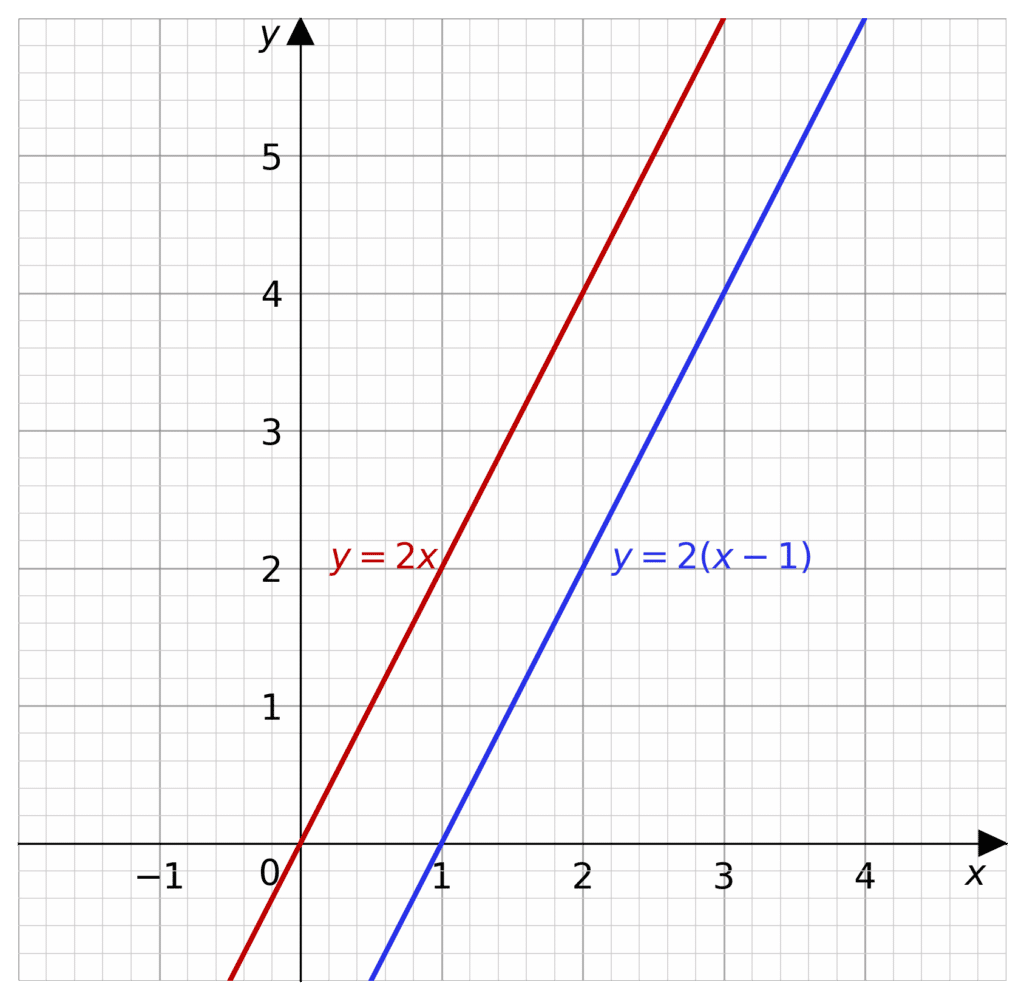
Horizontal translations move the graph left and right. This is along the x-axis.
Example: Shift the following graph right by one unit.
y=2x
So take an input, say x=2, which gives us y=4, then if we are to shift the graph right, then the input of x=3 must give us the same output y=4
We must then reduce the input by one, so instead of inputting x into the equation, we must input x-1, which gives us a new equation of
y=2(x-1)
To translate left, the same thing must happen, except the number of units you’re shifting left will be added to the input.
Remember you add to the input to translate left, and you subtract from the input to translate right. It can be a little bit counter-intuitive.
Vertical Translation
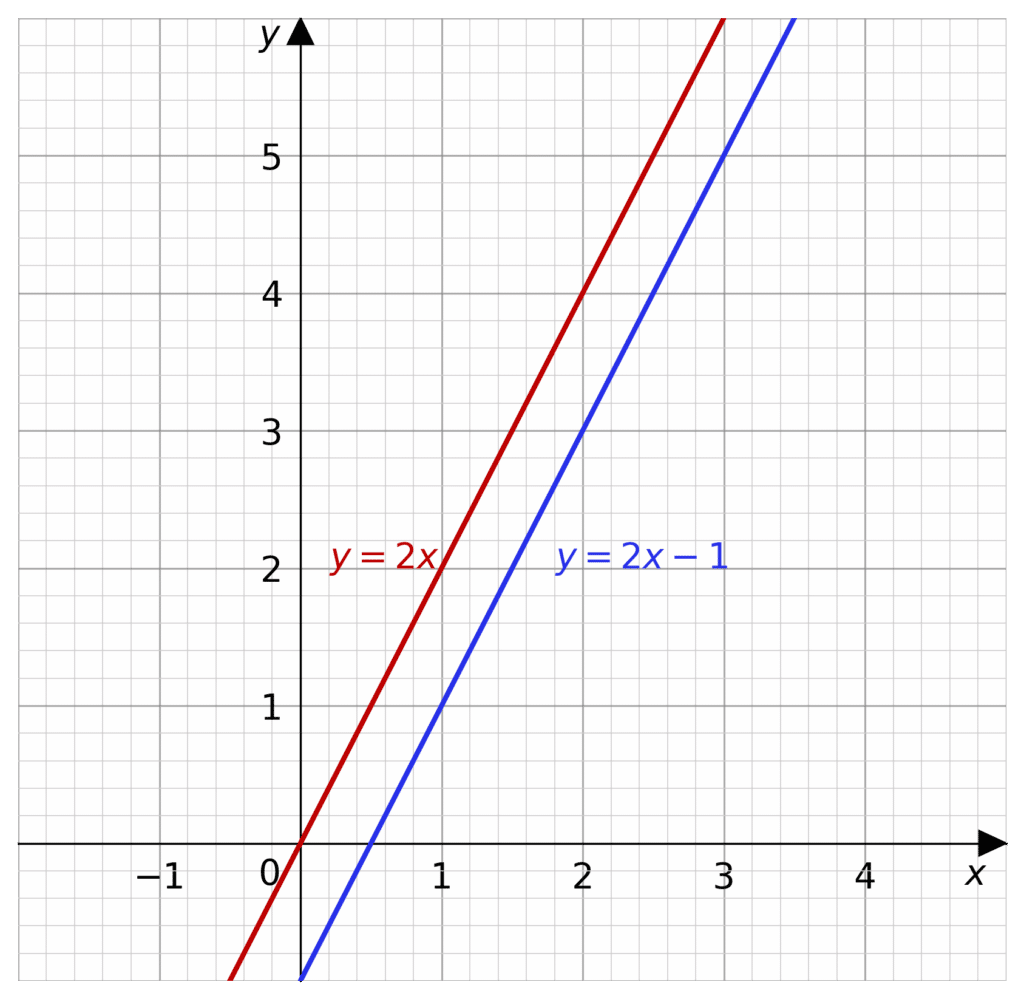
Vertical translations move the graph up and down. This is along the y-axis.
Let’s shift a graph up by one unit, and let’s choose this equation:
y=2x
Take the input x=2 which has output y=4, to shift the graph up by 1 all we have to do is add another 1 to the output, so that when x=2 the output is y=5
This gives us the new equation:
y=2x+1,
and if we want to translate down we simply subtract by however much we want to translate down by.
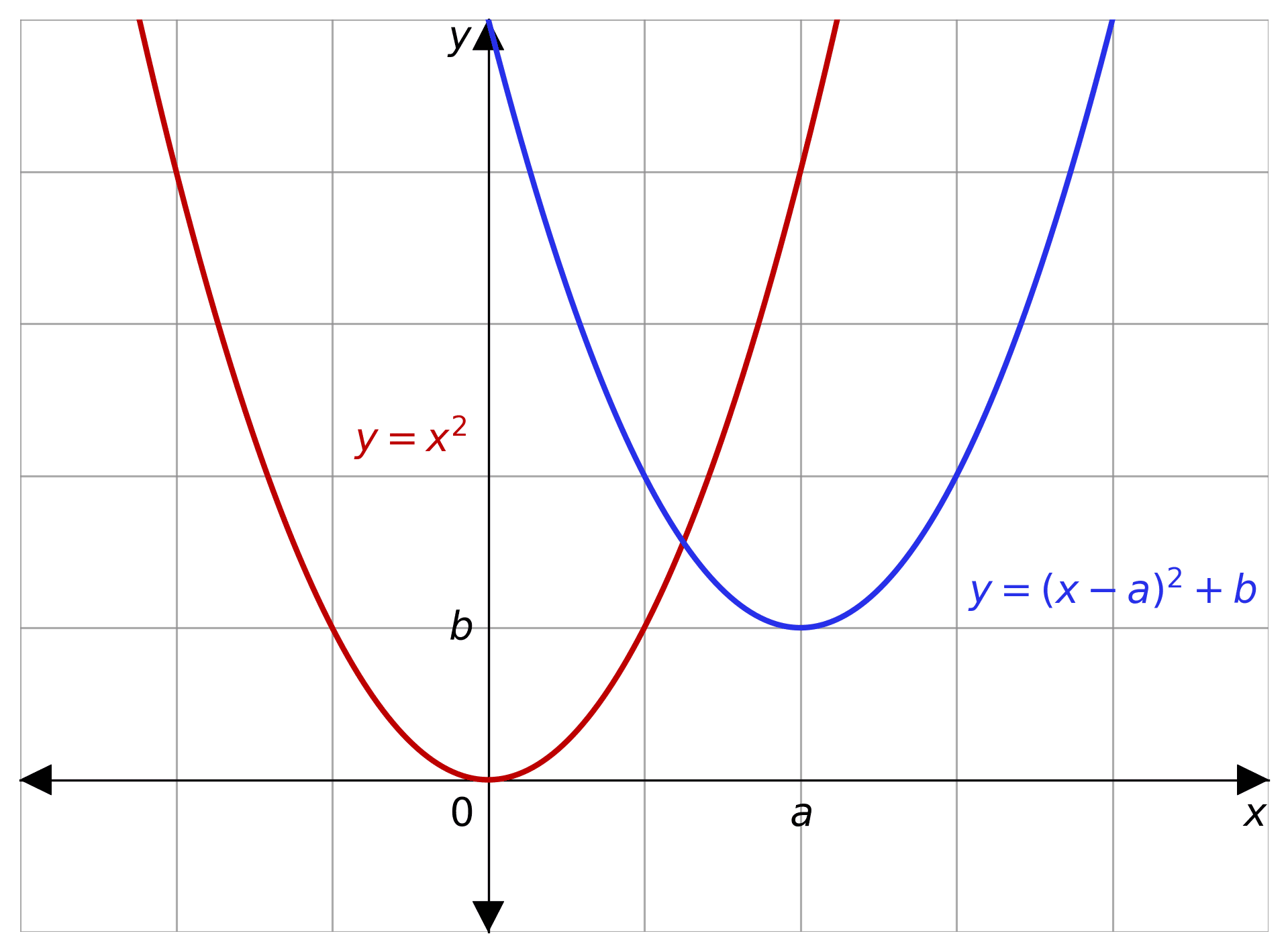
Translation by a Vector
We may write a translation in the form of a vector
\begin{pmatrix} a \\ b \end{pmatrix}
where the graph is translated right by a units and up by b units. For example, if we are to translate the equation
y=x^2
by the vector we can begin by the right translation, so we must subtract the input by a
y=(x-a)^2
then the up translation, adding b to the output, giving us a new graph equation
y=(x-a)^2+b
Reflections
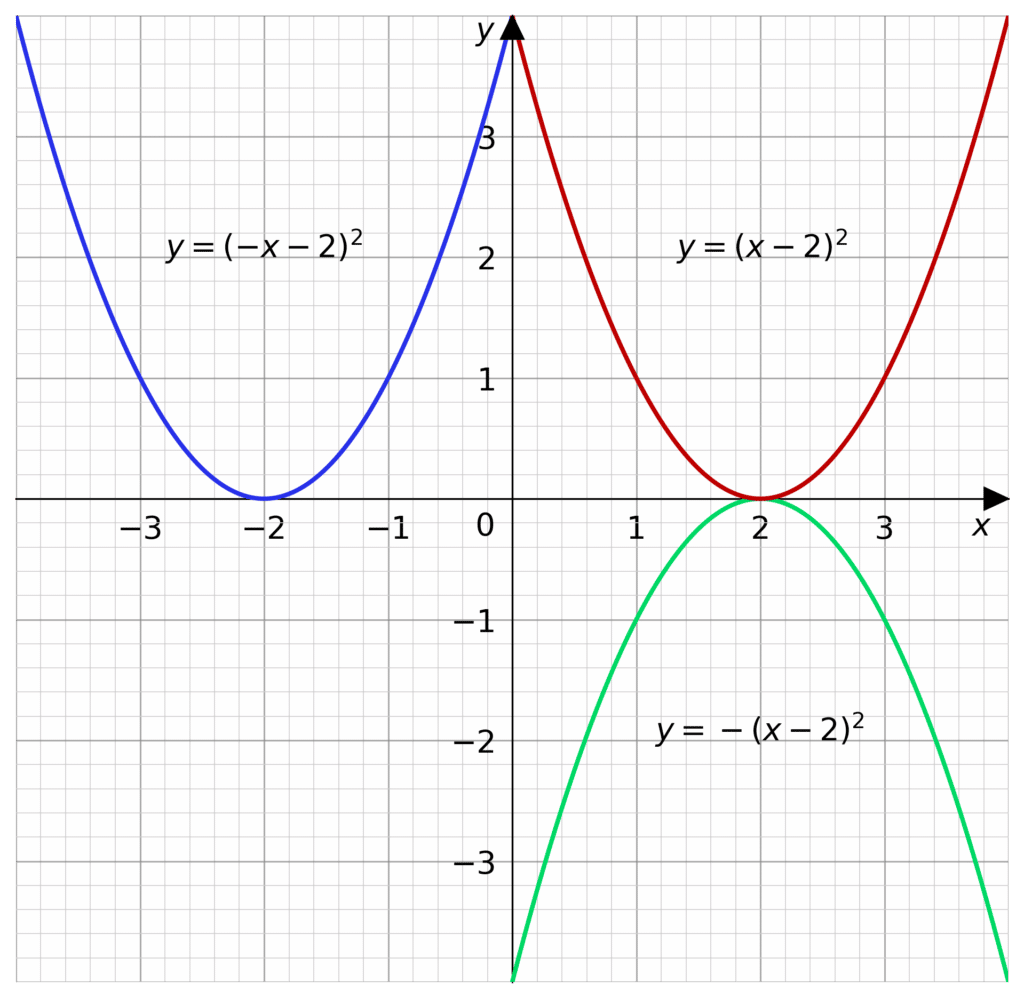
We will look at two reflections, a reflection over the y-axis, and a reflection over the x-axis. An easy way to visualise these is to imagine folding the graph along the axis and then imprinting the curve on the other side.
When reflected over the x-axis all positive y values become negative and all negative y values become positive, so the output of the equation must be multiplied by -1
For example y=\sqrt{x} reflected over the x-axis is y=-\sqrt{x}.
When reflecting over the y-axis all positive input (x) values become negative and all negative become positive. So the input must be multiplied by -1
For example y=3^x reflected over the y-axis is y=3^{-x}
The example picture is for y=(x-2)^2
Example 1: Transformation of a Point
Point A lies on a graph at coordinates (5, 6), find the coordinates of A after the following transformations
a) Translation by vector \begin{pmatrix} -3 \\ 2 \end{pmatrix}
b) Reflection over the y-axis
c) Reflection over the x-axis
[6 marks]
a) Firstly we recall that a vector translation tells us how it will move along the x-axis on the top row and how it will move along the y-axis on the bottom row. So in this case it translates the graph right by -3, or rather left by 3, and up by 2, which gives us
(5-3,6+2)=(2,8)
So the point corresponding to A is (2,8)
b) For a reflection over the y-axis the x variable is the one that becomes multiplied by -1, as the y-axis is vertical. So the new point, corresponding to A is (-5,6)
c) For a reflection over the x-axis the y variable is the one that becomes multiplied by -1, as the x-axis is horizontal. So the new point, corresponding to A is (5,-6)
Example 2: Transformations of Equations
The equation
y=\dfrac{1}{x}
is graphed. Find the equation for y after the following transformations
a) Translation by vector \begin{pmatrix} 4 \\ -2 \end{pmatrix}
b) Reflection over the y-axis
[4 marks]
a) With the vector we know that the graph is shifted right by 4 and down by 2, so to shift the equation right by 4 we must subtract the input by 4, giving us
y=\dfrac{1}{x-4}
Now, to shift down by 2 the output must be subtracted by 2, giving us a final equation of
y=\dfrac{1}{x-4}-2
b) For a reflection over the y-axis the input must be multiplied by -1, this gives us
y=\dfrac{1}{-x} = -\dfrac{1}{x}
Notice this is identical to a reflection on the x-axis.
Graph Translations and Reflections Example Questions
Question 1: A graph has only one turning point, at (5, -3).
a) The graph is translated, the turning point is now (7, 2), what is the translation vector?
[2 marks]
b) The original graph is translated by vector
\begin{pmatrix} -2 \\ 3 \end{pmatrix}
What are the new coordinates of the turning point?
[1 mark]
a) If we say the translation vector is
\begin{pmatrix} a \\ b \end{pmatrix}
then this means that the new coordinate for the turning point is (5+a, -3 +b), so solving the x-coordinate
5+a=7
a=2
And solving the y-coordinate
-3 +b = 2
b=5
So the translation vector is
\begin{pmatrix} 2 \\ 5 \end{pmatrix}
b) The new coordinates will be
(5-2, -3 + 3)
(3,0)
Question 2: A graph shows the equation
y=x^2-2x
Find the equation for y, in its simplest form, after the following transformations
a) A translation by the vector\begin{pmatrix} 4 \\ 1 \end{pmatrix}
[3 marks]
b) A reflection over the y-axis
[2 marks]
a) The translation vector shifts the graph right by 4. This means 4 must be subtracted from the input. Which gives us
y=(x-4)^2-2(x-4)
We also shift up by 1, so 1 must be added to the output
y=(x-4)^2-2(x-4)+1
Which expands out to
y=x^2-10x+25
or
y=(x-5)^{2}
b) A reflection over the y-axis means the input must be multiplied by -1. Which gives us
y=(-x)^2-2(-x)
As (-x)^2=x^2, we get
y=x^2+2x
Question 3: A graph shows the equation
y=3x^3-2x+3
Full describe the transformation from this equation to
a)y=-3x^3+2x+3
[2 marks]
b) y = -3x^3 +2x -3
[2 marks]
c) y=3(x-2)^3 -2(x-2) +1
[2 marks]
a) A reflection, over the y-axis.
b) A reflection, over the x-axis.
c) A translation by the vector \begin{pmatrix} 2 \\ -2 \end{pmatrix}
