Revise
Functions with Inputs and Outputs
Functions with Inputs and Outputs Revision
Functions
Using a function involves inputting values into a function machine, that produces an output. Function machines follow certain rules, transforming the input(s) into an output(s).
Function Machines
You will need to be able to understand and use function machines.
Here is a function machine:
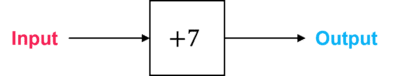
Inputs are put into the machine, and then the operation in the machine transforms the input into the output.
In this case, the operation is +7.
For example, if the input was 5
Input: 5
Operation: +7
So, 5+7=12
Output: 12
Equations as Function Machines
Equations can also be expressed as function machines.
For example,
y=2x
In this equation, the output y is reached through inputting a value of x and multiplying it by 2, or:
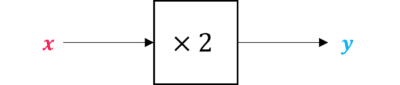
Composite Functions
A composite function is two functions done one after the other. This means that we take an input, put it through the first function, then use the output of the first function as the input for the second function.
Example: The function A is shown below.
The function B is shown below.
The function C is defined as the function A then the function B.
Find the output if 4 is the input for function C.
We start by putting our input, 4, through function A. The action for A is \times 4
4\times 4=16The output from A is 16, so the input for B will be 16
The action for B is -7
16-7=9The output from B is 9, so the output from the whole function C is also 9.
Example 1: Function Machines
Use the function machine to find the value of y when x is 32
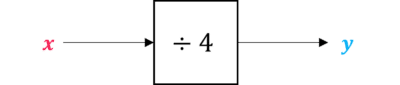
[2 marks]
x=32 is the input. To get to the output, we need to follow the operation in the function machine:
32\div4=8Therefore, y=8
Example 2: Function Machines with Multiple Boxes
Some function machines have more than one operation.
Use the function machine to find the value of y when x is 3.
[2 marks]
In this function machine, the input is x and the output is y.
We can solve this by doing one operation at a time.
We can see x goes through the operation \div 2 first, so:
3\div 2=\dfrac{3}{2}And then goes through +4. At this point, we don’t use the input 3, we use the output of the first operation, \dfrac{3}{2}. This is because in the diagram it shows that x does not directly go into +4, the output of the first operation does:
\dfrac{3}{2} +4=\dfrac{11}{2}Therefore, the final output, or y is \dfrac{11}{2}
Example 3: Function Machines as Equations
As well as creating function machines from equations, you may need to be able to recognise equations from function machines.
Find a formula for y in terms of x for this function machine.
[2 marks]
We’ll start at the beginning of the machine, x is inputted and divided by 2.
This means the equation will start with y = \dfrac{x}{2}
Then, the operation is +4, meaning \dfrac{x}{2}+4
Hence, the equation is:
y=\dfrac{x}{2}+4
Example 4: Inverse Functions
A number is inputted into the following function machine, and 12 is the output. Work out which number was inputted.
[3 marks]
This question involves an inverse function. This means, we will use the function machine backwards.
We start with the output, 12, and move right.
The next operation we reach is -36. However, as we are doing the opposite of the function machine, we do the opposite operation, so +36.
12+36=48Moving right again, we reach \times 4. The inverse of this would be \div 4
48\div 4 = 12Therefore, the input was 12
Example 5: Composite Functions
The function A is as follows:
The function B is as follows.
The composite function C is defined as the function A then the function B. Find the output of C if the input is 28.
[3 marks]
First we put 28 into function A
28-1=27
27\div3=9
So the output from function A is 9
Now we put 9, the output from function A, into function B
9+16=25
25\div5=5
So the output from function B is 4
Hence, the output from function C is 4
Functions with Inputs and Outputs Example Questions
Question 1:
(a) Design a function machine that outputs y from the input, x, from the equation
y=6(\sqrt{x}) + 3
(b) Use the function machine to work out y when x is 49.
[4 marks]
(a) The function machine would be
(b) Input =49
\sqrt{49}=7\\ 7\times6=42\\ 42+3=45\\ y=45
Question 2: Calculate the value of x when y = 16.
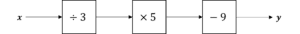
[3 marks]
This is an inverse function, so we use the opposite operations:
16 + 9 = 25\\ 25\div5=5\\ 5\times3=15\\ x=15Question 3: Find the missing operation in the following function machine.
[3 marks]
We need to find the operation that means the input 36 can reach the output 3.
If we start with the input, it is square rooted first:
\sqrt{36}=6But we do not know the next operation, so let’s go to the output and use the inverse function:
3^3=27So, we need to work out how you go from 6 to 27.
One way to reach 27 from 6, is +21
Therefore, a possible missing operation is +21
The operation could also be:
\times 4.5or,
\div \dfrac{2}{9}Question 4: A composite function C is formed by performing function A and function B, both shown below.
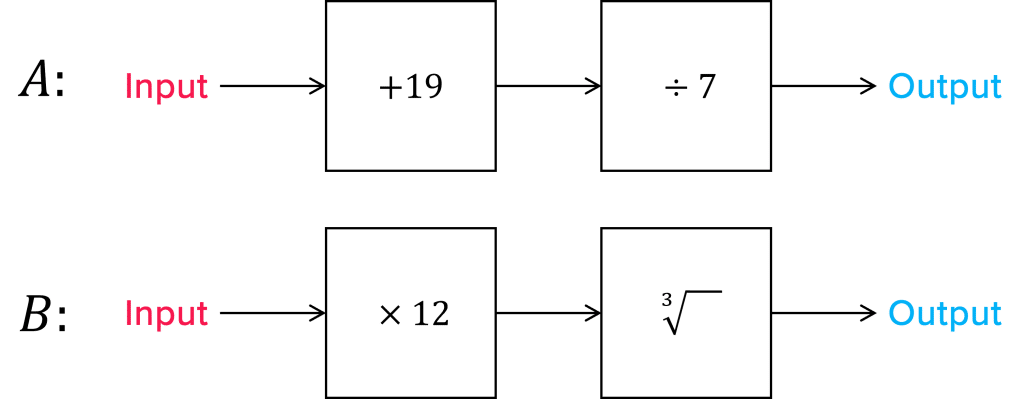
Find the output if 107 is the input for function C
[5 marks]
First, put 107 into function A
107+19=126
126\div7=18
So the output from function A is 18
Next, take 18, the output from function A, and put it into function B
18\times 12=216
\sqrt[3]{216}=6
So the output from function B is 6
Hence, the output from function C, with an input of 107, is 6
