Nets and Surface Area
Nets and Surface Area Revision
Nets and Surface Area
A net is a deconstructed 3D shape folded out flat. Nets can be helpful when we want to calculate the surface area of a 3D shape.
Skill 1: Nets of Cubes
A net shows us each face of a shape when it is laid out flat, and there are often many different nets for a 3D shape. Below are some examples of nets of cubes.

Note: these are only some of the nets of a cube – there are many more
Each of the nets above can be folded up to construct a cube, like so:
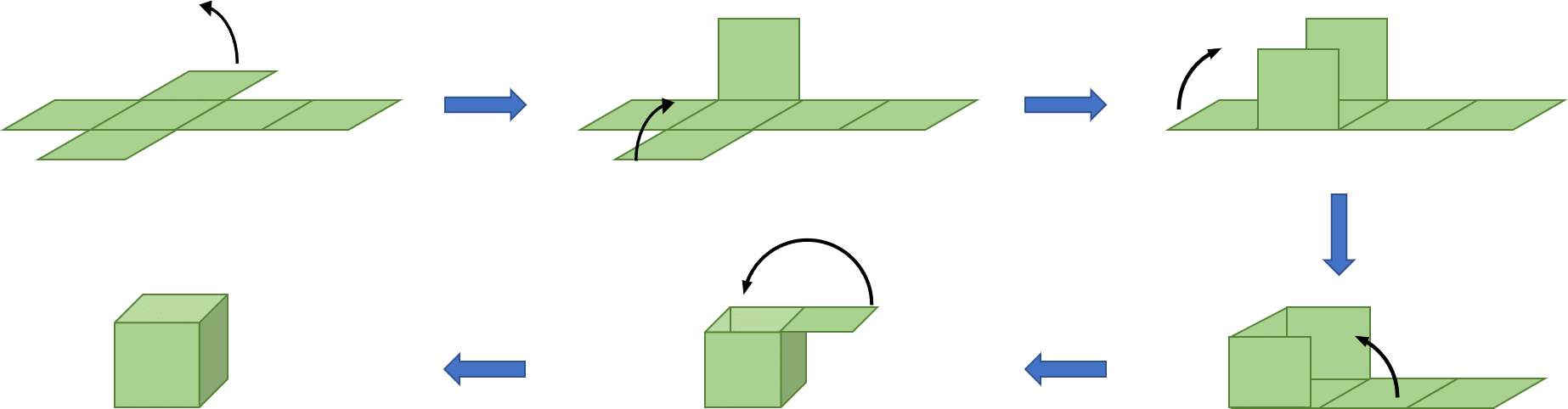
Cubes are the simplest nets you will encounter, so make sure you are comfortable drawing them before moving on to harder shapes.
Skill 2: Nets of Other Shapes
There are some other common shapes that you should familiarise yourself with, including prisms and pyramids.
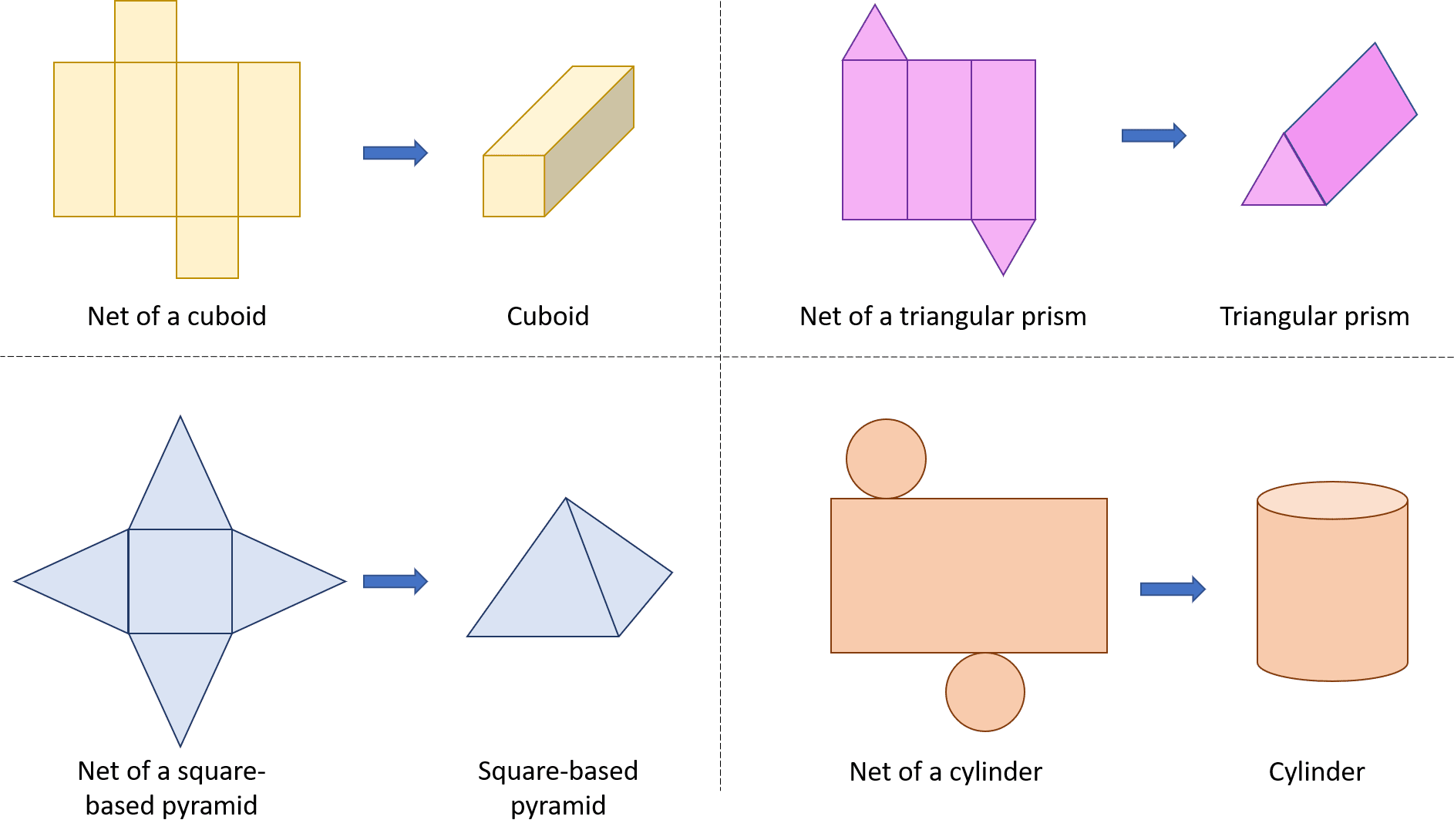
A prism is like a 2D shape ‘stretched out’ with the original 2D at either end. This makes drawing a net of a prism fairly simple, as it will feature the 2D shape at both ends with rectangles between them that form the ‘stretched out’ section. A cuboid is also a type of prism, so the net of a cuboid follows the same pattern.
A pyramid always features a 2D shape as its base, with each edge linked to a triangular face. These triangular faces all converge to a central point above the centre of the base. The nets of pyramids are easy to draw – just draw the shape of the base with triangles attached to each side.
A cylinder can be thought of as a circular prism. Its net follows the same pattern as the nets of prisms.
Some examples of nets of 3D shapes are shown below:
Skill 3: Finding the Surface Area
We can use nets to find the surface area of a 3D shape – the combined area of all the faces.
Consider the following net of a cuboid.
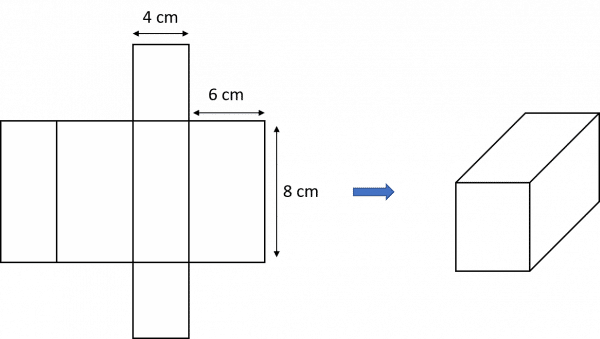
We can use the net to work out the surface area. There are 3 ‘pairs’ of faces that are the same – if we calculate the areas of these individual faces we can add them all up to get the surface area of the cuboid.
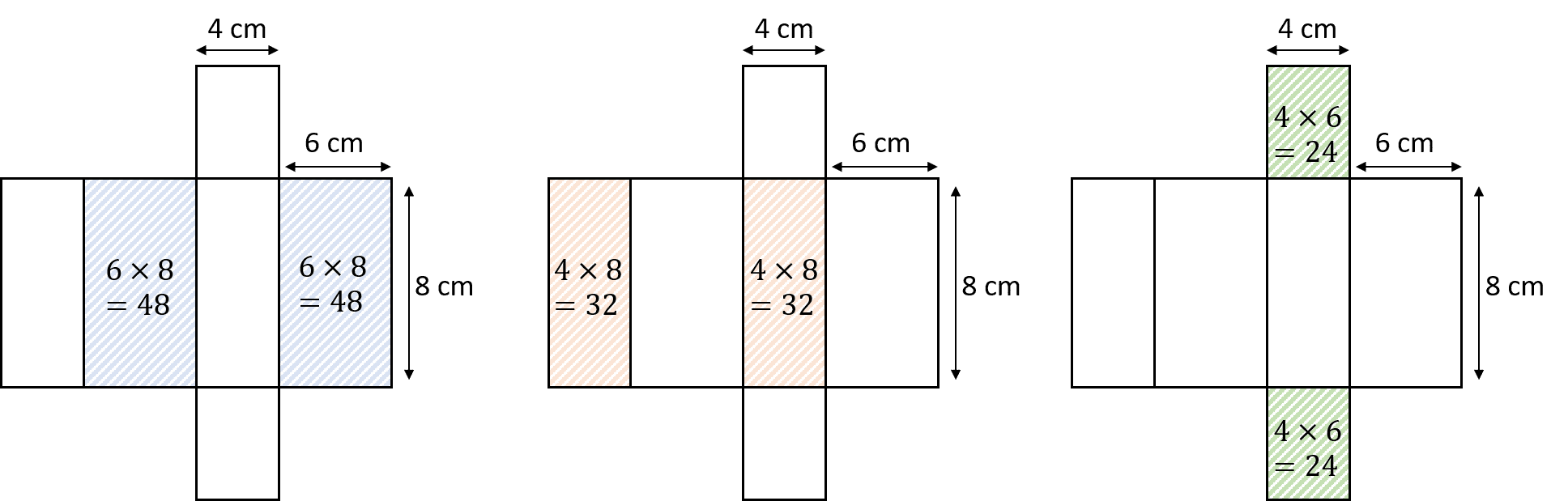
The total surface area is therefore:
2 \times48 + 2 \times32 + 2 \times 24 = 208 cm^2
Note: remember that the units of area are cm^2, m^2 etc.
Example: Surface Area of a Cylinder
Calculate the surface area of cylinder A from the net shown.
[3 marks]
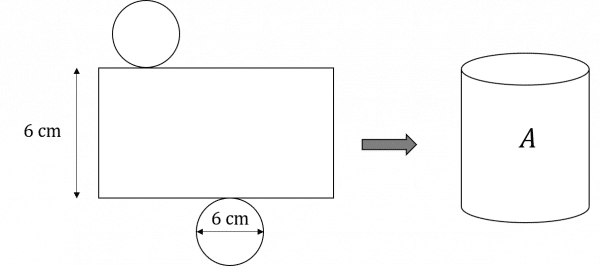
The diameter of the circular face is 6 cm, meaning the radius of the circle is 3 cm. We can calculate the area of one circular face using the formula:
Area of a circle = \pi r^2
So the area of both circular faces on the cylinder is:
2\times \pi \times 3^2=18\pi = 56.55 cm^2
To calculate the area of the rectangle, we need to know the length – this is the same as the circumference of the circle (2\pi r).
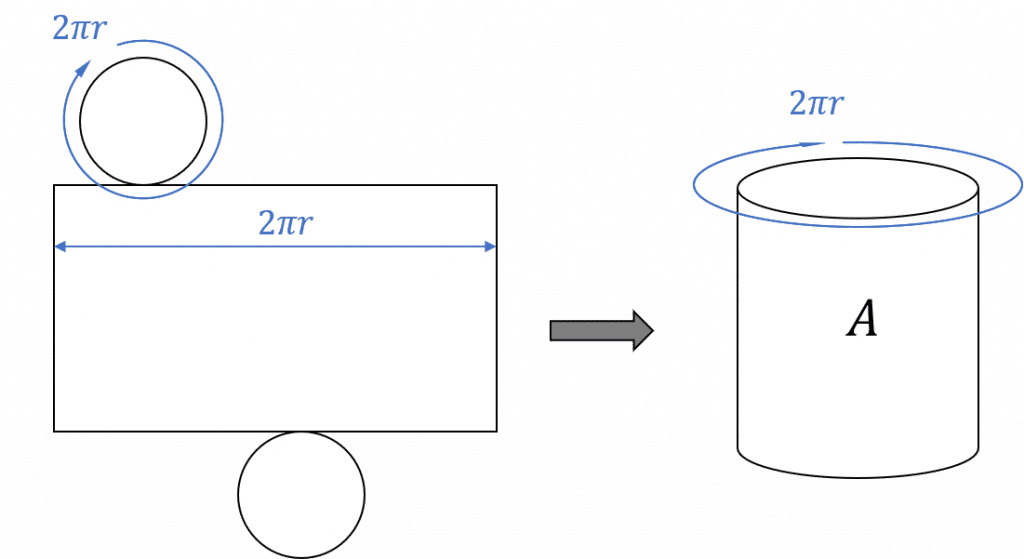

The length of the rectangle is therefore:
2\pi r = 6 \pi cm
We can now calculate the area of the rectangle face:
6 \pi \times 6 = 36 \pi = 113.10 cm^2
The total surface area of the cylinder is therefore:
\text{Area} = 56.55 + 113.10=169.65 cm^2
Note:
There is a simple formula for calculating the surface area of a cylinder:
Surface area of a cylinder =2\pi rh + 2\pi r^2
Where r is the radius of the circle face and h is the height of the cylinder.
Substituting values into this formula is a quick way of performing the calculations shown in the example above.
Nets and Surface Area Example Questions
Question 1: State which of the following nets can be used to form a cube.
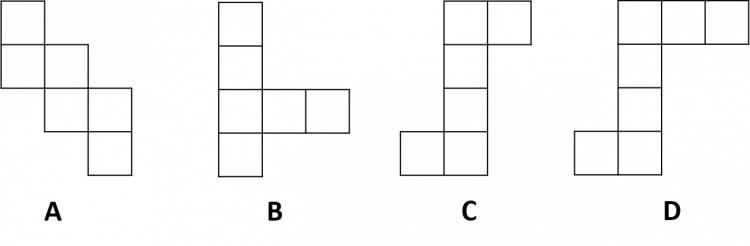
[2 marks]
Only nets A and C will form a cube.
The faces on net B will overlap when folded over and net D has too many faces.
Question 2: Sketch a net of the following cuboid and label all the measurements.
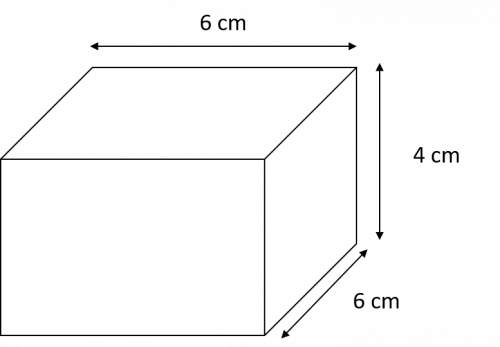
[3 marks]
Your completed sketch should look something like this:
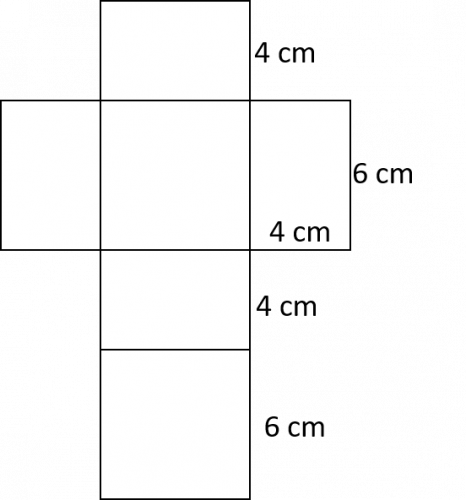
Question 3: Calculate the surface area of the triangular prism from the net shown.
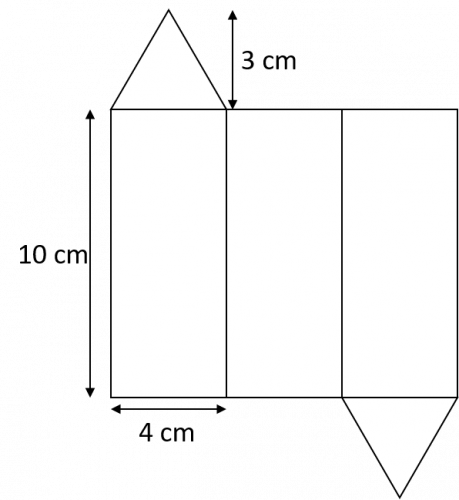
We need to use the following formula:
Area of a triangle =\dfrac{1}{2} \times \text{base} \times \text{height}
So the area of both triangular faces is:
2\times \dfrac{1}{2}\times4\times3 = 12 cm^2
The area of the three rectangular faces is:
3\times10\times4 = 120 cm^2
The total surface area is:
12+120=132 cm^2
Question 4: Calculate the surface area of the cylinder from the net shown.
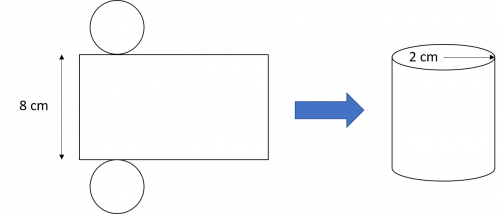
Use the formula and substitute in the values of r=2 and h= 8:
\begin{aligned}\text{Surface area} &= 2\pi r^2 + 2\pi rh \\ &=(2 \times \pi \times 2^2) + (2\times \pi \times 2 \times 8) \\ &= 8\pi + 32\pi \\ &= 25.13+100.53\\ &=125.66 \text{ cm}^2\end{aligned}
Question 5: Use the net of the square-based pyramid to calculate the surface area of the 3D shape.
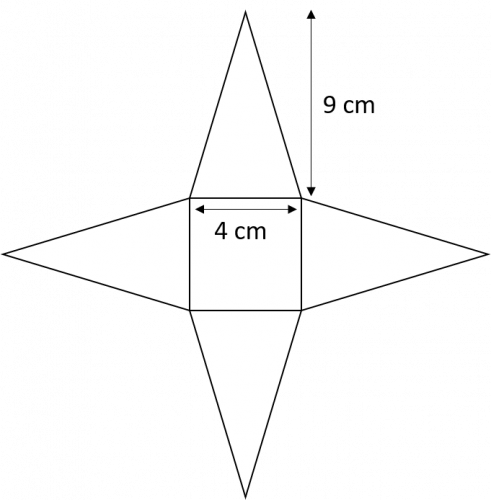
The surface area of the pyramid is given by:
\text{Surface area}= 4\times \text{area of triangle }+ \text{area of square base}
Use the formula for the area of the triangle:
\text{Area of a triangle}=\dfrac{1}{2} \times \text{base} \times \text{height}
Substitute in the values from the net (base =4 cm and height =9 cm) to calculate the area:
\begin{aligned}\text{Surface area} &= (4\times \dfrac{1}{2}\times4\times9) + (4\times4) \\[1.5em] &= 72+16 \\[1.5em] &= 88 \text{ cm}^2 \end{aligned}


