Negative Numbers
Negative Numbers Revision
Negative Numbers
Negative numbers (or minus numbers), denoted by a minus sign (-), are what we use to count below zero. For example, counting backwards from 3 looks like
3,\,\,2,\,\,1,\,\,0,\,\,-1,\,\,-2,\,\,-3,\,\,-4, ...
Skill 1: Using a Number Line
Before we head further into understanding negative numbers, let’s recall the following:
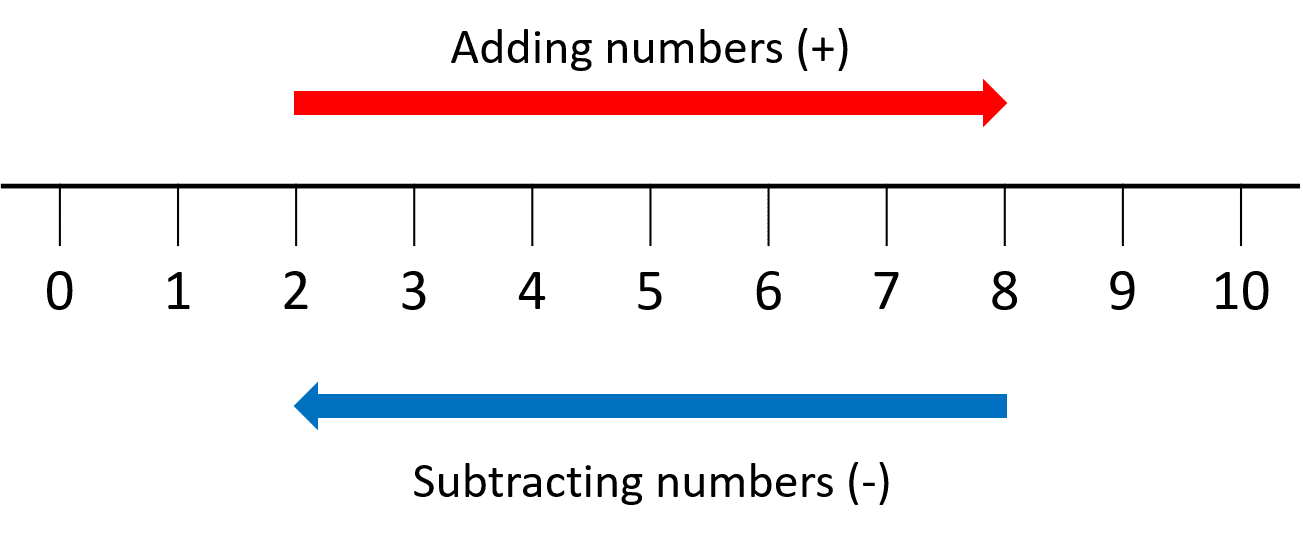
• To add values on a number line, we have to move to the right.
• To subtract values on a number line, we have to move to the left.
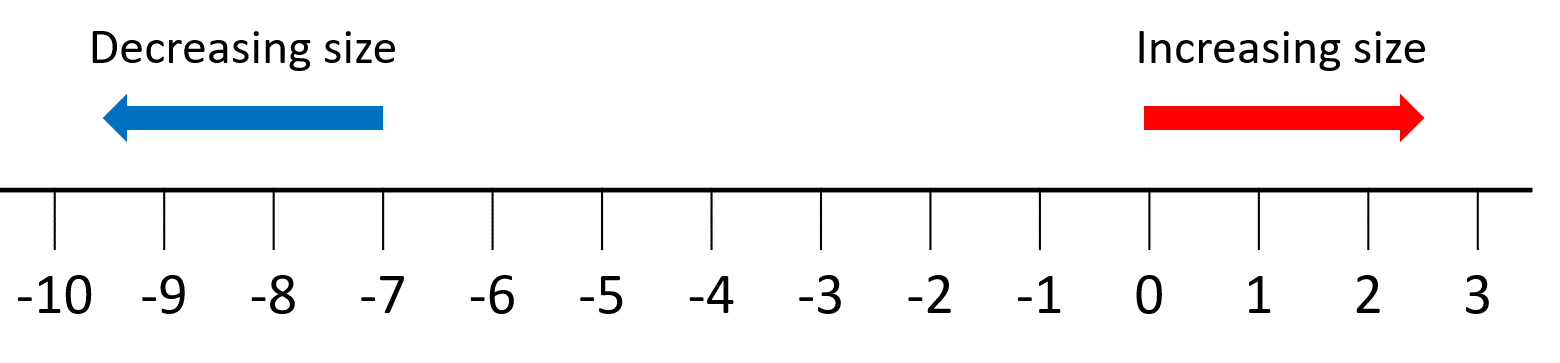
Skill 2: Ordering Negative Numbers
Just like positive numbers, negative numbers can be ordered by their size. The larger the number after the minus sign, the smaller the number.
This can be quite confusing, so it helps to use a number line:
Skill 3: Adding Negative Numbers
When we add a negative number, it is the same as taking away a positive number. For example:
\begin{aligned}5+(-2) &= 5-2 \\&=3\end{aligned}
Skill 4: Subtracting Negative Numbers
When we subtract a negative number, it is the same as adding a positive number. For example:
\begin{aligned}100-(-25) &= 100+25 \\&=125\end{aligned}
Skill 5: Multiplying Negative Numbers
When multiplying negative numbers, treat the calculation as if the numbers are positive. Then, there are two rules to remember:
- When we multiply a positive number by a negative number (and vice-versa), the answer is always negative. For example:
2\times-3 = -6
- When we multiply a negative number by a negative number, the answer is always positive. For example:
-5\times-7=35
Skill 6: Dividing Negative Numbers
When dividing negative numbers, treat the calculation as if the numbers are positive. Then, there are two rules to remember:
- When we divide a positive number by a negative number (and vice-versa), the answer is always negative. For example:
12 \div -4 = -3
- When we divide a negative number by a negative number, the answer is always positive. For example:
-48 \div -6=8
Example 1: Using a Number Line
Use a number line to work out the following:
a) 5+3
b) 8-4
[2 marks]
a) Locate the number 5 on a number line, then move 3 values to the right:
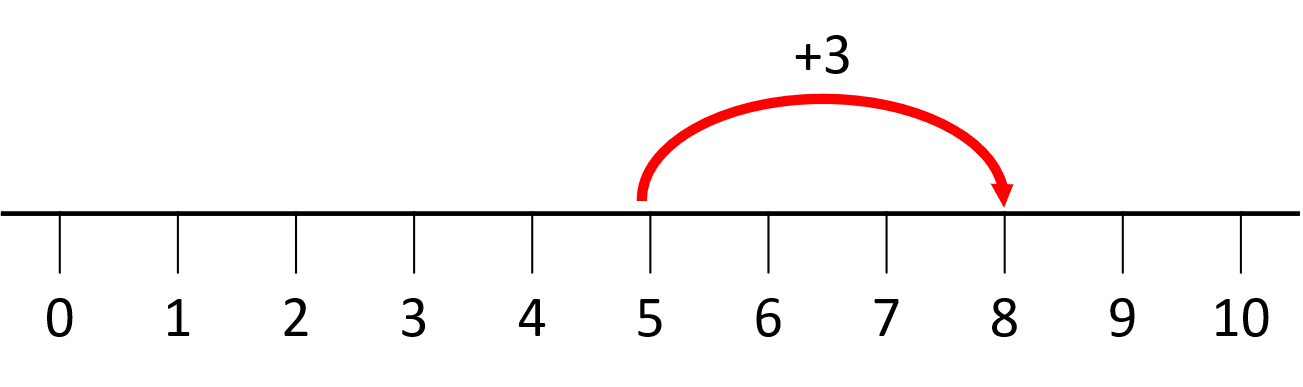
Answer: 5+3=8
b) Locate the number 8 on a number line, then move 4 values to the left:
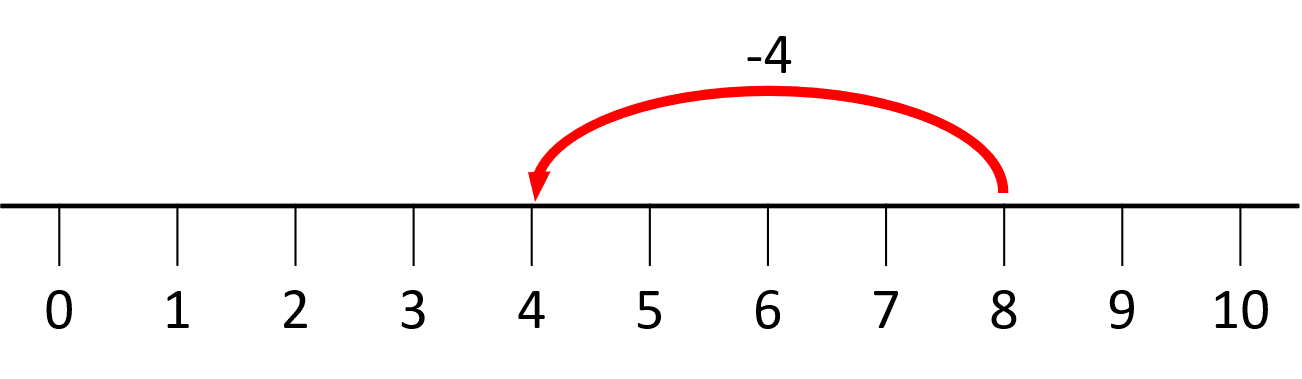
Answer: 8-4=4
Example 2: Ordering Negative Numbers
Put the following numbers in decreasing order of size:
-35, -8, -28, -40, -2, -17
[2 marks]
First, draw a suitable number line. We need our number line to include each of the numbers above:

Next, we have to add the numbers into their correct positions:
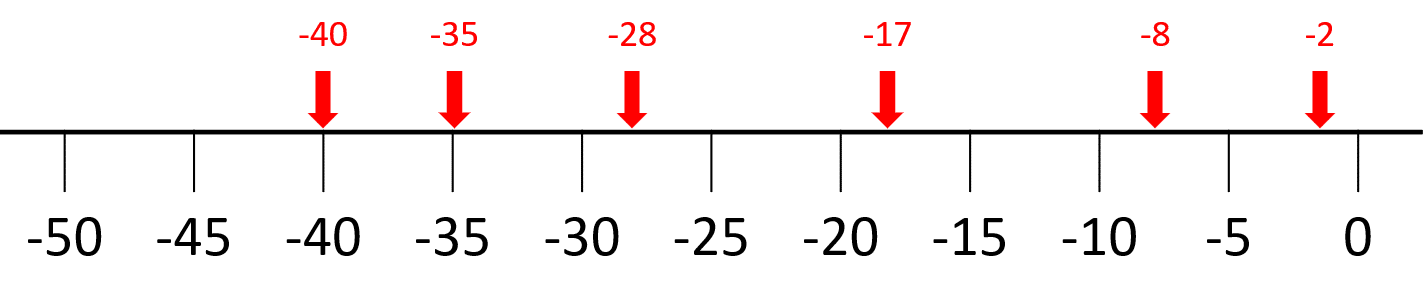
We have to put the numbers in decreasing order of size, which means we need to list them from right to left.
Answer:
-2, -8, -17, -28, -35, -40
Example 3: Adding and Subtracting Negative Numbers
Calculate the following:
a) 55+(-33)
b) -105 - (-28)
[3 marks]
a) We can use a number line to make this calculation easier – remember that adding a negative number is the same as subtracting a positive number. Our calculation can be rewritten as:
55-33
On the number line, starting from 55 we will move 33 values to the left:
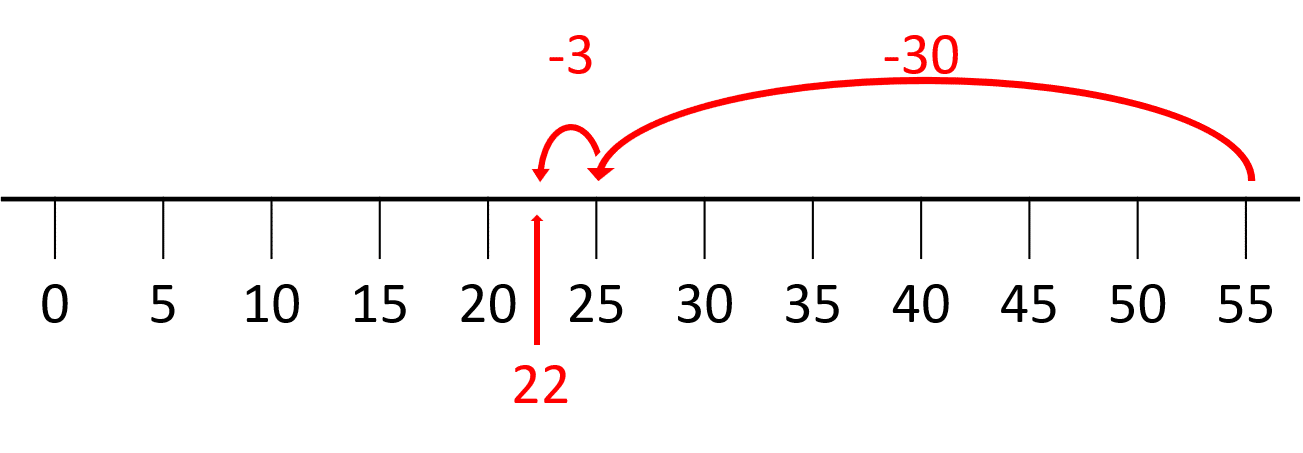
Answer: 55+(-33) = 55-33 = 22
b) Remember that subtracting a negative number is the same as adding a positive number. Our calculation can be rewritten as:
-105 + 28
On the number line, starting from -105 we will move 28 values to the right:
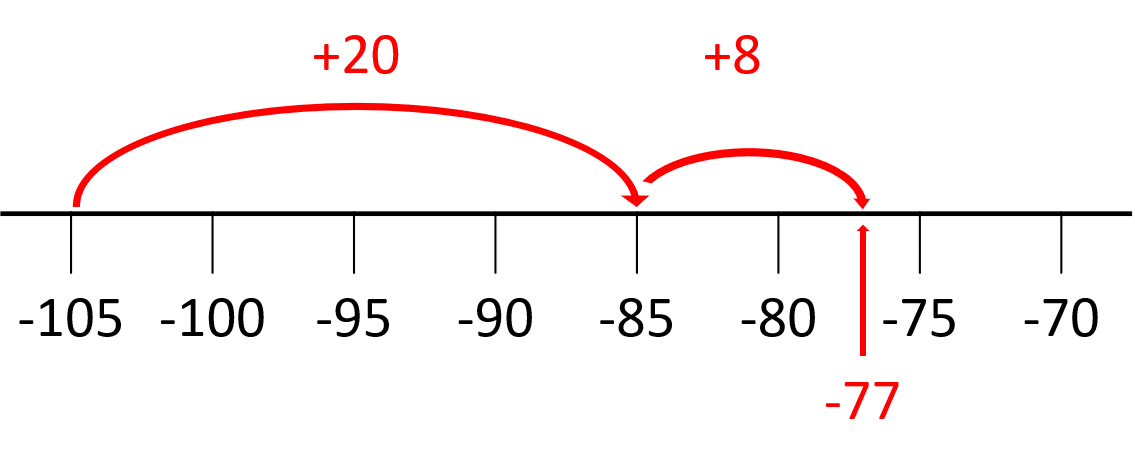
Answer: -105 + 28 = -77
Example 4: Multiplying and Dividing Negative Numbers
Calculate the following:
a) 24 \times - 4
b) 90 \div -10
[3 marks]
a) Perform the calculation as if the numbers were positive: 24\times4 = 96
Then remember that multiplying a positive number by a negative number gives a negative, so the answer is:
24\times-4=-96
b) Perform the calculation as if the numbers were positive: 90\div10 = 9
Then remember that dividing a positive number by a negative number gives a negative, so the answer is:
90 \div -10 = -9
Notes:
You are encouraged to use a number line to perform calculations with negative numbers, but you do not have to use them if you are comfortable without.
Negative Numbers Example Questions
Question 1: Evaluate the following:
a) 3-(+7)
b) 7-(-2)
c) -1-(-6) (tricky!)
[3 marks]
a) These are two different signs so it must be a subtraction:
3-(+7)=3-7
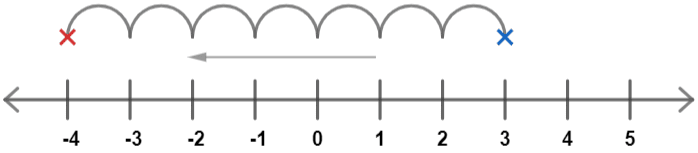
Finding 3 on a number line and moving 7 to the left, we get
So, the answer is 3-(+7)=-4
b) These are two of the same signs so it must be an addition:
7-(-2)=7+2
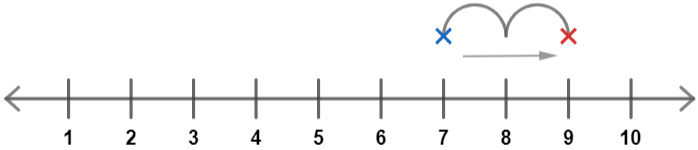
Finding 7 on a number line and moving 2 to the right, we get
So, the answer is 7-(-2)=9
c) In this calculation we have two of the same signs so it must be an addition.
Note: the minus sign in front of the 1 does not change. It has no bearing on whether the calculation becomes an addition or a subtraction. So, the calculation is
-1-(-6)=-1+6
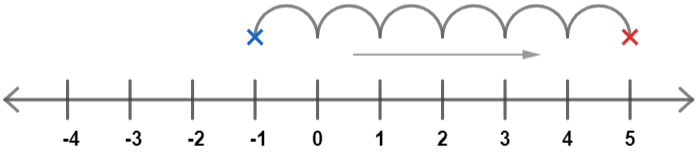
Finding -1 on a number line and moving 6 spaces to the right, we get
So, the answer is -1-(-6)=5
Question 2: Evaluate the following:
a) -5\times 7
b) -18 \div 3
c) -4 \times (-10)
[3 marks]
a) We are multiplying one negative and one positive, so the answer must be negative. Given that
5\times 7=35
We get that
-5\times 7=-35
b) We are dividing one negative and one positive, so the answer must be negative. Given that
18\div 3=6
We get that
-18\div 3=-6
c) We are multiplying two negatives, so the answer must be positive. Given that
4\times 10=40
We get that
-4\times (-10)=40
Question 3: Put the following numbers in increasing order of size:
-2, 8, 15, -20, -13, 0
[2 marks]
Draw a suitable number line:

Next, mark the numbers on the number line:
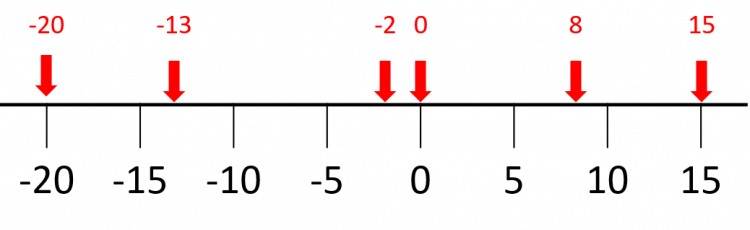
Finally, put the numbers in increasing order of size by listing them from left to right.
Answer:
-20, -13, -2, 0, 8, 15