Money
Money Revision
Money
This page covers all areas of money and finance that you need to be familiar with, including personal/household finance, budgeting, utility bills, exchange rates.
Money Problems
Often you will be required to work out the cost of transactions in real world scenarios, usually working out the total cost or amount of change needed. You will need to be comfortable with using the adding, subtracting, multiplying and dividing with integers and decimals.
Example:
Emily and Chloe go to a café, they buy
2 cups of tea at £1.25 each
3 muffins at £2.40 each
2 sandwiches at £2.50
They pay with a £10 and £5 note.
Work out how much change they will be given.
Total cost:
2\times £1.25 + 3\times £2.40 + 2\times £2.50 =£14.70Change:
£15-£14.70=£0.30
Unit Pricing
The unit price of an item is the cost of the product for a fixed quantity. For example, the unit price of pasta might be 12\text{p} per 100\text{ g}.
It is often useful to look at the unit price when comparing products, as it helps you accurately compare the value ignoring any deals or differences in sizes.
\text{Unit price}=\dfrac{\text{price}}{\text{mass}}
Example:
A small local shop sells two different sizes of chocolate bars:
90\text{ g} chocolate bar – £1.05
220 \text{ g} chocolate bar – £2
Which chocolate bar is better value for money?
Comparing each chocolate bar per gram.
Small chocolate bar – \dfrac{1.05}{90}\times 100=1.17 pence per gram
Large chocolate bar – \dfrac{2}{220}\times 100 = 0.91 pence per gram
Therefore, the large chocolate bar is better value for money.
Profit and Loss
The definition of profit is the money made after any expenses are taken into account.
To work out the profit, you subtract the total expenses away from the revenue.
Example:
The table below shows some information of some items sold in a shop during a day.

Complete the table and calculate the total profit made on these items.
Calculator – £12\div 6=£2 profit on each item
Cost =£4.50-£2=£2.50
Pack of pencils – £4 \div 8=£0.50 profit on each item
Sale price =£0.70+£0.50=£1.20
Pack of pens – £5.60 \div (£1.80-£1)=7 (quantity)
Notebooks – 3\times (£3.50-£1.90)=£4.80 profit
Total profit =£12+£4+£5.60+£4.80=£26.40
Bank Accounts
The two most common types of bank accounts are current accounts and savings accounts.
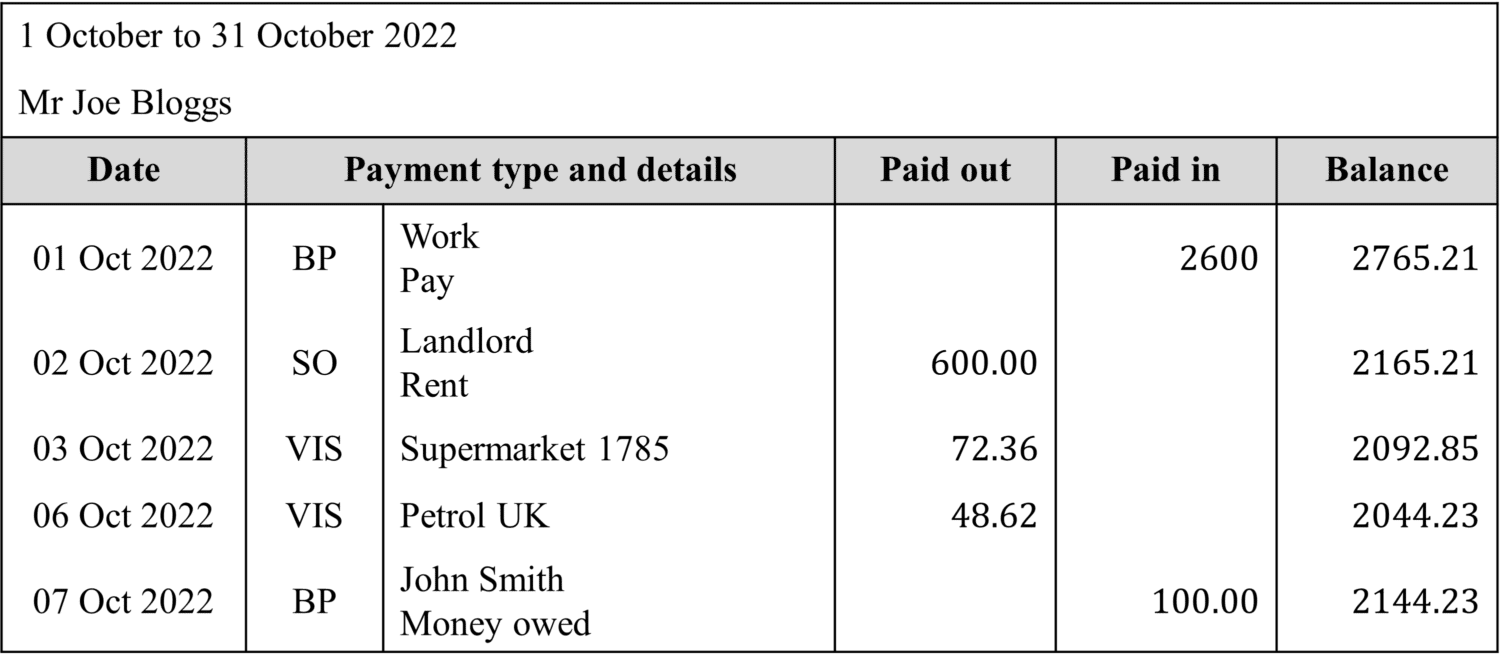
A current account is ordinarily used on a daily basis to pay for bills and make purchases, the ingoing and outgoing money then appears on a monthly statements, showing the method of transaction, the amount of money and where the money is going/from. The statements for current accounts often look similar to the image shown below.
Savings accounts are accounts intended for people to deposit money into to save part of their income, of which the bank will pay additional money into the account depending on the amount in the savings account. This is called interest, which is set as a percentage that can vary between banks. Most savings accounts pay compound interest, which is further explained on Compound Growth and Decay.
Example:
Here is a part of Isabel’s latest bank statement.
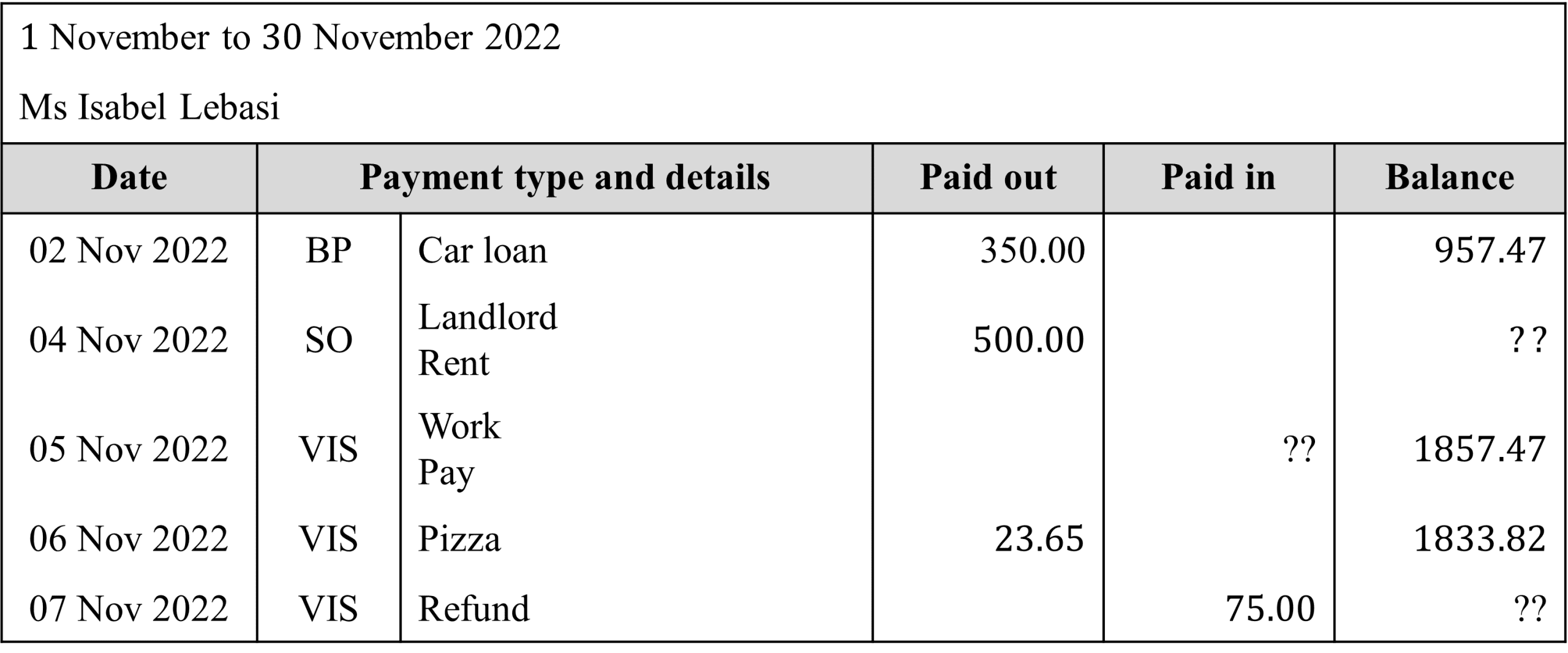
Using the bank statement, work out how much Isabel got paid on the 5th of November and what her final balance was on the 7th of November.
To work out how much Isabel got paid we first need to work out what her balance was on the 4th of November.
£957.47-£500=£457.47Then to work out how much she was paid we can subtract this balance from her balance after she was paid.
£1857.47-£457.47=£1400Finally to work out her final balance we need take add her final ‘paid in‘ amount to her previous balance.
£1833.82+£75=£1908.82
Loans, Credit and Hire Purchase
A loan is when you borrow money from a bank, building society or lender. Upon repaying the loan, interest will also have to be paid on top of the amount that needs to be paid back. The more time it takes a person to repay the loan, the more interest they have to pay, the terms and rate of interest will be outlined when the loan is taken out. Interest on a loan is calculated similarly to a savings account, however instead of receiving money, the person with the loan will pay the bank.
Another form of borrowing money is to use a credit card, which will be used to make purchases and can be paid off within a certain time period with no interest applied. However, if the amount owed is not paid back within the set time period, the interest rate can usually be substantially higher than loans through banks and building societies. Credit cards usually have enticing new customer deals in an attempt to get you to sign up, therefore it is important to fully understand what the terms and conditions are past any introductory rates.
Hire purchase is a method of buying items that are typically more expensive than goods you would buy on a regular basis, for example a car or laptop. To buy the item you would usually have to pay an initial deposit and then the remaining amount due would be paid in monthly instalments over a set period of time. In most cases, this method of purchase will mean that the customer ends up paying more for the product compared to if they paid for it upfront, due to interest or additional charges.
Example:
Harrison takes out a £4500 loan to buy a car, with a rate of interest of 6\% per year.
How much interest will he pay after 1 year?
£4500\times 0.06=£270
Annual Rates – AER and APR
Annual Equivalent Rate (AER)
AER is a rate of interest that is calculated on a yearly basis taking into account compound interest. Therefore, it takes into account interest accrued previously, so in a savings account for example it will take into account interest earned on your interest.
The formula for AER is:
\textcolor{#f43364}{\text{AER}}=\left(1+\dfrac{\textcolor{#f21cc2}{r}}{\textcolor{#00bfa8}{n}}\right)^n-1
\textcolor{#f21cc2}{r}= interest rate as a decimal
\textcolor{#00bfa8}{n}= number of time the interest is paid in one year
Annual Percentage Rate (APR)
The APR given for mortgages, loans and credit cards factor in additional charges and costs as well as the interest rate. This allows people to easily compare rates between different lenders, without having to factor in extra charges.
Usually when you see an APR figure advertised for a loan, this is just the representative APR. This means that not everyone will be able applicable for this rate, depending on credit checks conducted by the lender. The current rule on representative APR is that a minimum of 51\% of customers who apply must get the advertised representative APR.
The actual APR you get is called your personal APR, which may vary substantially from the representative APR.
Example:
Jamie wants to open a savings account and sees an account that offers 6.5\% interest paid on a monthly basis.
Calculate the AER of this account to 2 decimal places.
Using the formula for AER:
\left(1+\dfrac{0.065}{12}\right)^{12}-1=0.066971852To convert to a percentage, multiply by 100:
AER =6.70\% to 2 decimal places.
Wages and Salaries
Wage and salary are slightly different forms that people are paid for working.
If you are paid based on the number of hours you work per day or week, this is known as a wage. Your hourly pay will be set by the company you work for based on a set amount of hours, which may sometimes increase if you work outside of these standard working hours, which is known as overtime.
A salary is a fixed amount of money, which will be set each year and paid in equal monthly payments. Employees who are paid in this way are usually in professional jobs, like teachers or doctors. Ordinarily, a salary doesn’t change based on the number of hours you work in a given time period.
Example:
At a supermarket employees are paid 1.5 times their normal hourly pay if they work overtime and 2 times their normal hourly pay for working overtime on Sundays.
Aoife is contracted to work 30 hours from Monday to Saturday, at an hourly rate of £10.20.
One week she works 45 hours, including a 6 hour shift on Sunday.
Calculate how much Aoife earns for that week.
First calculate how much she gets paid for working her standard hours each week.
30\times £10.20=£306Then calculate how much she gets paid for her Sunday shift.
6\times 2 \times £10.20=£122.40Finally, calculate how much she gets paid for her remaining overtime.
9\times 1.5 \times £10.20=£137.70So Aoife has earned £306+£122.40+£137.70=£566.10
VAT and Tax
Income Tax
Income tax is a financial contribution that you make on money that your earn. The first £12570 of your earnings per year isn’t taxed (as of 2022), this is called your personal allowance.
There are three tax bands for income greater than £12570:
Basic rate – 20\% tax for earnings between £12571 and £50270
Higher rate – 40\% tax for earnings between £50271 and £125140
Additional rate – 45\% tax for all earnings above £125140
Example:
Taylor earns £80000 per year.
To calculate how much income tax she pays, we need to split her income into the tax bands.
£12570 is tax free
£50270-£12570=\textcolor{#10a6f3}{£37700} is taxed at a rate of \textcolor{#10a6f3}{20\%}
£37700\times 0.2=\textcolor{#10a6f3}{£7540}
£80000-£50270=\textcolor{#10a6f3}{£29730} is taxed at a rate of \textcolor{#10a6f3}{40\%}
£29730\times 0.4=\textcolor{#10a6f3}{£11892}
Total income tax =£7540+£11892=\textcolor{#10a6f3}{£19432}
Budgeting
Budgeting is an important way of managing your finances taking into account all incomings and outgoings. A good method to budget your personal finances would be to write down all your outgoings within a month and compare this to your regular monthly income. It is often sensible to overestimate the amount of money you spend when budgeting, to reduce the risk of going overbudget. Budgeting is also very useful for planning trips and events, as they allow you to know how far in advance you may have to start saving money, or allow you to know your financial limitations so you don’t overspend.
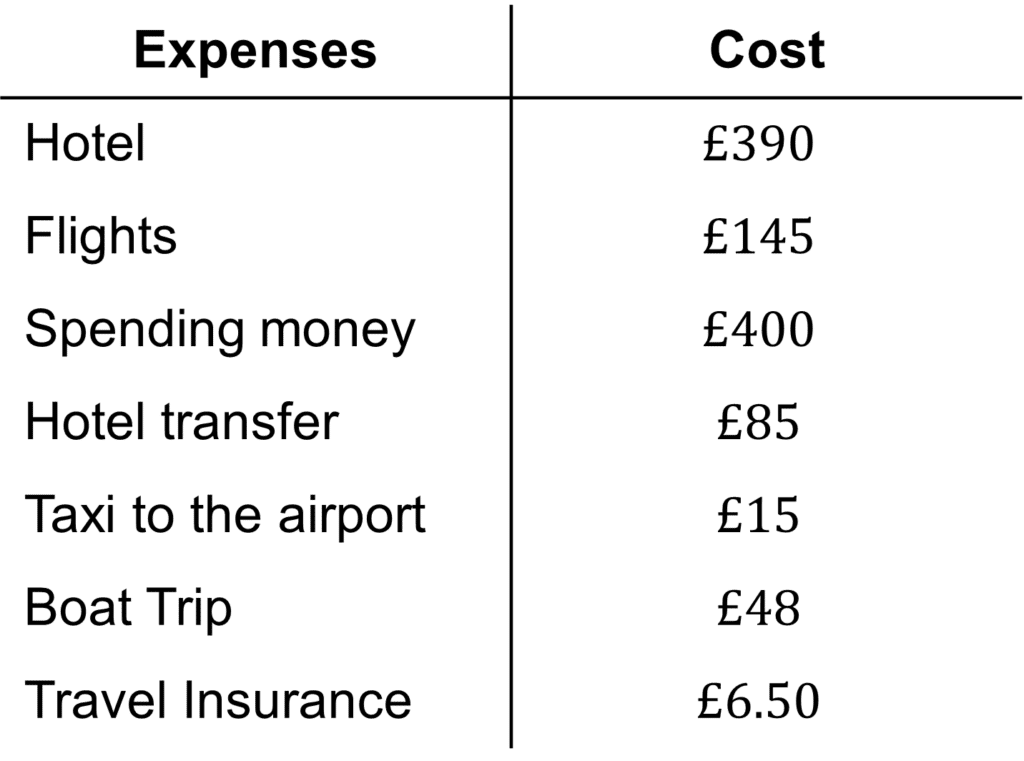

Example:
Here is an example of Holly’s planned costs for her upcoming holiday.
If she wanted to save £200 per month for this holiday, after how many months would she have enough to cover her expenses?
As a result of outlining her planned expenses, she knows that she needs to budget at least £390+£145+£400+£85+£15+£48+£6.50=\textcolor{#10a6f3}{£1089.50} for this trip.
Therefore, if she saves £200 per month, she will need to save for 1089.50\div 200=5.4475 \rightarrow \textcolor{#10a6f3}{6} months.
Utility Bills
When living in a property, in addition to mortgage or rent payments, you will also need to cover the costs of services like gas, electricity and water, which are usually paid each month or every 3 months.
The utility companies measure the amount of gas, electricity or water that have been used per month, this is either done using a smart meter or by the bill payer reading the meter themselves. On utility bills the current and previous readings will be shown, so to calculate the cost of your most recent bill you will need to subtract your previous reading from the current one, and then multiply it by the cost per unit.
There will also often be a standing charge added, to cover any additional costs.


Example:
The table on the right shows the water and electricity readings at the start and end of a 3 month period.
The water company charges \textcolor{#10a6f3}{46\text{p}} per \text{m}^3 of water plus a \textcolor{#10a6f3}{£15} standing charge per quarter.
The electricity company charges \textcolor{#10a6f3}{16\text{p}} per \text{kWh} of electricity plus a \textcolor{#10a6f3}{£6} monthly standing charge.
Calculate the total bill for water and electricity for this 3 month period.
Water:
First we need to subtract the previous reading from the current reading.
8400-7500=\textcolor{#10a6f3}{900 \text{ m}^3} of water used
So the cost of water used is 900\times £0.46+£15=\textcolor{#10a6f3}{£429}
Electricity:
Subtracting the previous reading from the current reading,
12350-10600=\textcolor{#10a6f3}{1750 \text{ kWh}} of electricity used
Therefore, the cost of electricity used is 1750\times £0.16+(3\times £6)=\textcolor{#10a6f3}{£298}
Thus, the total bill of water and electricity is £429+£298=\textcolor{#10a6f3}{£727}
Mortgages
As buying a house will often be the most expensive purchase someone can make, often people will need to borrow money to buy one. This type of loan is called a mortgage which will be spread out for many years, depending on a person’s age. Similarly to other loans, you will have to pay interest on top of the amount of money you have borrowed, paid monthly. The interest rate can either be set as a fixed rate for a certain number of years or it can vary depending on the rate set out by the bank. The longer it takes you to repay the mortgage, the more total interest you will pay.
How are mortgages calculated?
The amount you are able to borrow from a bank is directly proportionate to how much you get paid, and it will usually be 2.5 times greater than your salary. For two people applying for a mortgage, the amount that can be borrowed is calculated by multiplying the larger salary by 2.5 and then adding the smaller salary.
Example:
A couple want to buy a house together. One of them earns £21000 per year and the other earns £24000 per year.
If they have a deposit of £16000, can they afford a house valued at £100000?
Calculating the amount the couple can borrow:
2.5\times £24000 + £21000=\textcolor{#10a6f3}{£81000}Adding their deposit:
£81000+£16000=\textcolor{#10a6f3}{£97000}, so they cannot afford to buy this house.
Foreign Money and Exchange Rates
All countries’ currencies have varying values, so we often have to convert them to compare them to the British pound (£).
The table below shows the exchange rates for various currencies to the pound (£).
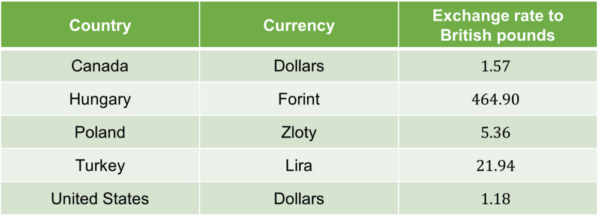
To convert from British pounds you need to multiply by the exchange rate.
For example to convert from pounds to American dollars, multiply by 1.18.
To go from American dollars to British pounds, you would need to divide by 1.18.
Note: Exchange rates are constantly changing, so you will be given the exchange rate to use in exam questions.
Example:
Using the table above convert £50 into Turkish lira.
50\times 21.94=1097 Turkish lira.
Money Example Questions
Question 1: Jack goes to a petrol station and buys 25 litres of petrol costing £1.62 per litre.
He also buys a chocolate bar and a bottle of water costing £0.85 and £1.40 respectively.
Work out the total cost of his purchases.
[2 marks]
Cost of petrol:
25\times £1.62=£40.50
Total cost:
£40.50+£0.85+£1.40=£42.75
Question 2: Justin is trying to decide whether he should buy a pack of 24 cans of cola for £12.50 or 2 litre bottles of cola, costing £1.80 each. Each can contains 330\text{ ml} of cola.
Which product offers better value for money?
[3 marks]
Unit price of 24 cans =\dfrac{£12.50}{24\times 330}\times 100=0.16 pence per \text{ml}
Unit price of 2 litre bottles =\dfrac{£1.80}{2000}\times 100=0.09 pence per \text{ml}
Therefore, the bottles of cola are better value for money.
Question 3: Rosie is looking to open a new current account. She looks at two different banks that have new customer deals.
Bank A offers her a 7\% bonus for her initial deposit, up to £2500.
Bank B offers a monthly gift of £9.50 for the first 12 months.
Rosie is going to make an initial deposit of £2400.
Which bank should she choose if she wants to have the most money in her account after 12 months?
[2 marks]
Bank A:
£2400\times 1.07=£2568Bank B:
£2400+12\times £9.50=£2514Therefore, Rosie should choose bank A.
Question 4: Molly is going to take a £2000 loan to go travelling.
The lender offers 4\% representative APR, however when she applies for the loan she is offered a personal APR of 5.2\%.
How much more does the personal APR cost compared to the representative APR?
[2 marks]
Representative APR:
£2000\times 1.04=£2080
Personal APR:
£2000\times 1.052=£2104
Difference:
£2104-£2080=£24Question 5: Veronica works at a bakery and is paid £11.25 per hour. She is paid 1.5 times more on weekends.
This month she works 170 hours, which includes 42 hours working on weekends.
She wants to save 60\% of her earnings (without taking into consideration tax) this month to pay for an upcoming holiday, which she has budgeted for as shown below.

Will she be able to save enough to pay for the holiday?
[4 marks]
First calculate how much Veronica is paid this month:
£11.25\times (170-42) + £11.25\times 1.5\times 42=£2148.75
60\% of £2148.75=£1289.25
Holiday expenses:
£650+£106+£300+£165=£1221Therefore, she will have saved enough to pay for the holiday.
Question 6: The table below shows the prices of two different electricity companies.

For a household that uses 8000 \text{ kWh} of electricity per year, which company should they choose?
[2 marks]
Northern Electricity:
8000\times £0.13 +4\times £20=£1120
Powered:
8000\times £0.14+£28=£1148Thus, they should choose Northern Electricity.
Question 7: Steve is going on holiday to Mexico and is going to take £450 in spending money, which he needs to convert into Mexican pesos (MXN).
A bank offers him an exchange rate of £1= 22.45 \text{ MXN}
If Steve returns home with 2694 \text{ MXN}, how much did he spend in pound sterling whilst on holiday?
[2 marks]
Converting 2694 \text{ MXN} into pounds:
2694\div 22.45=£120So he spent £450-£120=£330

MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now



