Volume of 3D Shapes
Volume of 3D Shapes Revision
Volume of 3D Shapes
The volume of a shape is a measure of how much space it occupies.
Volume of Prisms
The volume of a prism can be calculated as follows:
\text{Volume of prism}=\textbf{\textcolor{red}{area of cross section}} \times \textbf{\textcolor{blue}{length}}
This formula can be used for any form of prism, this includes, but is not limited to, cubes, cuboids and cylinders.
\text{Volume of a Cuboid}=\textbf{\textcolor{red}{Width}} \times \textbf{\textcolor{red}{Height}} \times \textbf{\textcolor{blue}{Length}}
This can be simplified for a cube since all three measurements are equal:
\text{Volume of a Cube}=\textbf{\textcolor{red}{Width}}\textcolor{red}{\boldsymbol{^3}}
\text{Volume of a Cylinder}=\textcolor{red}{\boldsymbol{\pi r^2}} \times \textbf{\textcolor{blue}{Length}}
Notice the use of \boldsymbol{\textcolor{red}{\pi r^2}} because the cross section is circular.
This can be expanded to more complex prisms.
Example: The diagram below shows a triangular prism. Work out the volume of the shape.
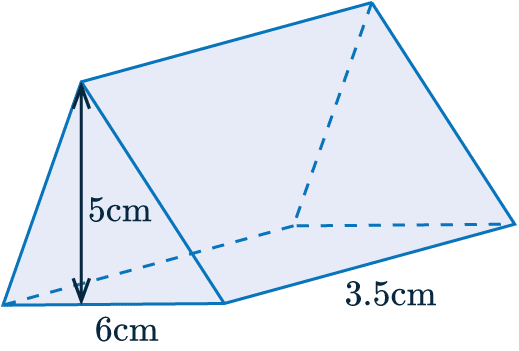
Firstly, find the cross section. As this is a triangular prism, this just entails finding the area of a triangle.
\text{Area of Cross Section}=\textcolor{red}{\frac{1}{2} \times 5 \times 6 =15} \text{ cm}^2
Thus,
\text{Volume of the prism }=\textcolor{red}{15}\times \textcolor{blue}{3.5}=52.5\text{ cm}^3 (3 sf)
Volume of a Sphere
The formula for the volume of a sphere, which can be found on the formula sheet, is as follows:
\text{Volume of a Sphere}=\frac{4}{3}\pi r^3
Example: The diagram below shows a sphere with a radius of 5 \text{ cm}
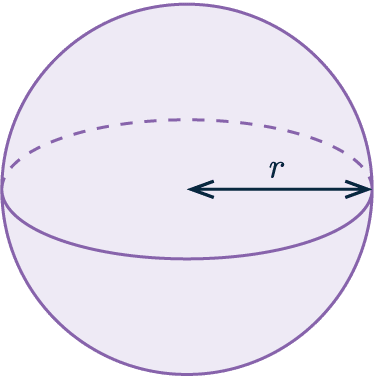
Work out the volume of the sphere.
Give your answer to 4 significant figures.
We are given that the radius is 5 \text{cm}, we simply need to substitute this into the formula.
\text{Volume of a sphere} = \frac{4}{3} \pi (5)^3 \approx 523.6 \text{ cm}^3 (3 sf)
Volume of Cones and Pyramids
The formula for the volume of a cone, which can be found on the formula sheet, is as follows:
\text{Volume of cone }=\frac{1}{3} \times \textcolor{red}{\pi r^2} \times \textcolor{blue}{\text{ perpendicular height}}
The formula for the volume of a pyramid, which is not on the formula sheet, is as follows:
\text{Volume of pyramid }=\frac{1}{3}\times\textcolor{red}{\text{ area of base }}\times\textcolor{blue}{\text{ perpendicular height}}
Example: The diagram below shows a square-based pyramid.
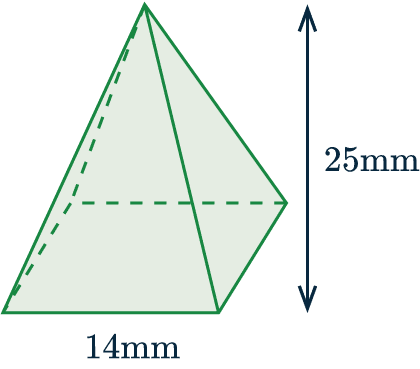
Determine the volume of the pyramid.
In this instance, the base is square. So the area of the base is simply:
\textcolor{red}{14} \times \textcolor{red}{14} = \textcolor{red}{196} \text{ mm}^2
So,
\text{Volume of pyramid }=\frac{1}{3}\times\textcolor{red}{196}\times\textcolor{blue}{25} \approx 1633.33 \text{ mm}^3
Volume of 3D Shapes Example Questions
Question 1: Shown below is a trapezoidal prism.
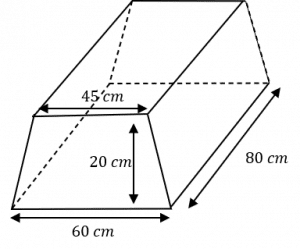
Calculate the prism’s volume.
[3 marks]
Firstly, we need to calculate the cross sectional area.
The cross section is a trapezium, so \frac{a+b}{2}h must be used.
\frac{45+60}{2} \times 20 =1050 \text{ cm}^2
Next, we must multiply by the length of the prism.
1050 \times 80 = 84000 \text{ cm}^3
Question 2: The diagram below shows a square-based pyramid.
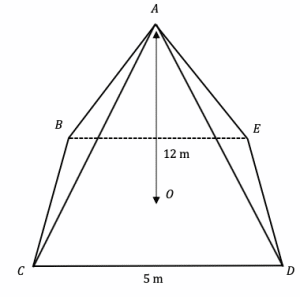
Find the volume of the pyramid.
[3 marks]
The volume for a square-based pyramid is calculated using the following formula:
\text{Volume }=\frac{1}{3} \times \text{base} \times \text{height}
The base area is simply a square, so:
5\times5=25 \text{ cm}^2
The volume is:
\text{Volume }=\frac{1}{3} \times 25 \times 12=100\text{ m}^3
Question 3: Shown below is a triangle based pyramid.
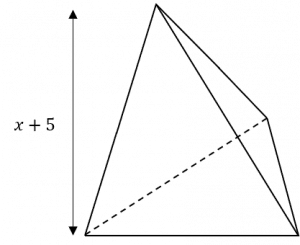
The base of the pyramid has an area of 18 \text{ cm}^2. The vertical height of the pyramid is x+5 \text{ cm}^2 and the volume is 54 \text{ cm}^2
Work out the value of x
[4 marks]
The formula for the volume of a pyramid is:
\text{Volume }=\frac{1}{3} \times \text{base} \times \text{height}
This results in:
\frac{1}{3}\times 18 \times (x+5)=6(x+5)
Setting this equal to the known volume results in a linear equation:
6(x+5)=54
Which can be solved as follows:
6(x+5)\div6=54\div6
x+5=9
x=9-5=4\text{ cm}
Question 4: Shown below is a composite shape, formed by joining a hemisphere to the top of a cylinder.
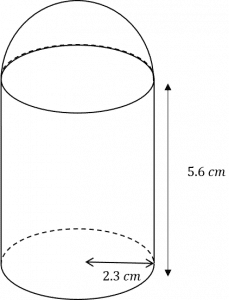
The cylinder and the hemisphere share the same radius, 2.3 \text{ cm}
The height of the cylinder is 5.6 \text{ cm}
Find the volume of the compound shape.
Give your answer to 3 significant figures.
[4 marks]
To begin with, simply imagine this as two separate shapes. First we will find the volume of the cylinder using:
\text{Volume of a Cylinder} = \pi r^2 \times \text{ height}
This results in:
\pi \times 2.3^2 \times 5.6= 29.624 \pi \text{ cm}^3
This has been left in terms of \pi for the sake of accuracy.
Next calculate the volume of the hemisphere, which is simply half a sphere:
\text{Volume of a Hemisphere}= \frac{1}{2} \times \frac{4}{3} \pi r^3
Resulting in:
\frac{1}{2} \times \frac{4}{3} \pi \times 2.3^3=8.111\pi \text{ cm}^3
Finally, add the two volumes together:
8.111\pi + 29.624 \pi =119 \text{ cm}^3 (3 sf)
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.