Vectors
Vectors Revision
Vectors
Vectors are quantities that are defined by both magnitude and direction. They are often used to describe where points are, or how to get from one corner of a shape to another.
You will need to use and understand vectors, as well as be able to add, subtract, and multiply them.
Vector Notation
There are several ways a vector can be represented, so it’s important you are familiar with them all to prepare for your exams.
Bold / Underlined
The most common way you’ll see is a letter written in bold, for example, these two lines are vectors:

For example, the vector \boldsymbol{b} is in the direction of the pink arrow.
Note: when you are writing in your exam, as you can’t write in bold, you will be expected to underline vectors, like: \underline{a}
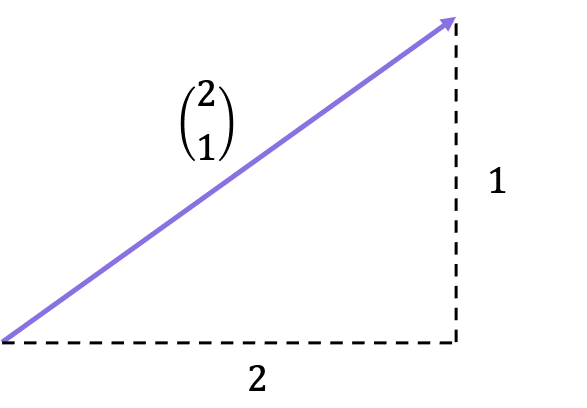
Column Notation
Vectors may also be displayed in columns:
Example: The column vector \begin{pmatrix}2 \\ 1\end{pmatrix} means 2 spaces to the right and 1 space up.
If you had \begin{pmatrix}-2 \\ -1\end{pmatrix}, this would mean 2 spaces to the left and 1 space down.

Arrow
Finally, you may see vectors written like:
\overrightarrow{AB} which is the vector between point A and point B
\overrightarrow{OC} which is the vector between the origin and point C
Note: The point O almost always represents the origin in vector questions.
Adding and Subtracting Vectors
When adding and subtracting using diagrams, it is important to pay attention to the direction the vector arrow is going.
A vector \boldsymbol{a} is positive in one direction, and if you flip the direction (point the arrow towards the opposite direction), the vector is now \boldsymbol{-a}:

Adding
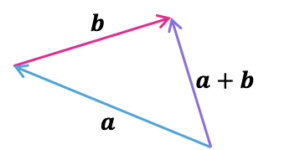
If we have two vectors, \boldsymbol{a} and \boldsymbol{b}, these can be added:
\boldsymbol{a}+\boldsymbol{b}
\boldsymbol{a}+\boldsymbol{b} will follow a route from the start of the \boldsymbol{a} arrow, to the end of the \boldsymbol{b} arrow, both in the positive direction:
Subtracting
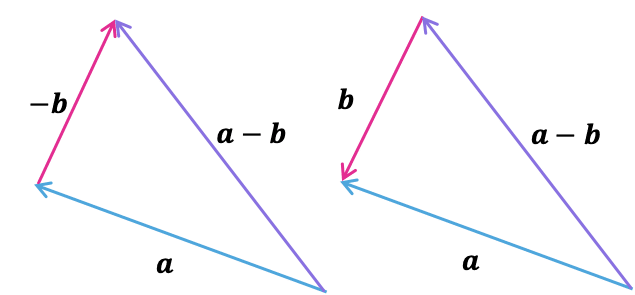
For subtraction, for example,
\boldsymbol{a}-\boldsymbol{b}
The \boldsymbol{b} is negative, so either of these diagrams correctly portray this subtraction:
Adding and Subtracting Column Vectors
Column vectors are easy to add and subtract, because you just treat the top row and the bottom row as separate sums, for example:
\begin{pmatrix}5 \\ 2\end{pmatrix}+\begin{pmatrix}3 \\ 1\end{pmatrix}=\begin{pmatrix}5+3 \\ 2+1\end{pmatrix}=\begin{pmatrix}8 \\ 3\end{pmatrix}
\begin{pmatrix}6 \\ 4\end{pmatrix}-\begin{pmatrix}2 \\ 3\end{pmatrix}=\begin{pmatrix}6-2 \\ 4-3\end{pmatrix}=\begin{pmatrix}4 \\ 1\end{pmatrix}
Multiplying Vectors by a Scalar
Multiplying vectors by a scalar simply means multiplying vectors by a number (not a vector).
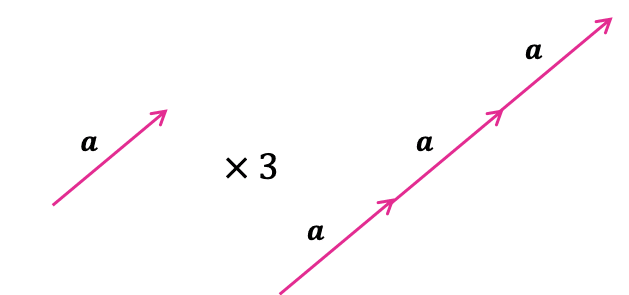
For example,
\boldsymbol{a}\times3=3\boldsymbol{a}
This is represented in the diagram:
If we have a vector containing more than one letter, we just multiply each letter by the scalar:
3\times(\boldsymbol{a}+\boldsymbol{b})=3\boldsymbol{a}+3\boldsymbol{b}
Similarly, in column vector form:
4\times\begin{pmatrix}3 \\ 2\end{pmatrix}=\begin{pmatrix}4\times3 \\ 4\times2\end{pmatrix}=\begin{pmatrix}12 \\ 8\end{pmatrix}
Vector Magnitudes
The magnitude of a vector is the length of a vector.
Magnitude has no direction, so is always positive.
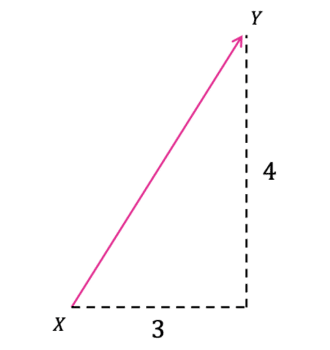
Example:
Find the magnitude of the vector
\overrightarrow{XY}=\begin{pmatrix}3 \\ 4\end{pmatrix}
Looking at the diagram, we can work out the length of the vector \overrightarrow{XY} by treating it as a right-angled triangle and using Pythagoras’ theorem:
\sqrt{4^2+3^2}=5
Example 1: Finding Vectors
Express the vector \overrightarrow{XZ} in terms of \boldsymbol{a} and \boldsymbol{b}
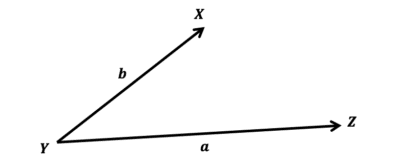
[2 marks]
So, let’s start at X. We will have to go through Y to get to Z.
To get from X to Y, we have to go in the negative direction of \boldsymbol{b}, so
\boldsymbol{-b}
Then, we will have to go from Y to Z, which is \boldsymbol{a} in the positive direction,
\boldsymbol{+a}
So, in total:
\boldsymbol{-b}+\boldsymbol{a}
Or,
\boldsymbol{a}-\boldsymbol{b}
Example 2: Vectors on Parallel Lines
Express the vectors \overrightarrow{AB} and \overrightarrow{AD} in terms of \boldsymbol{a} and \boldsymbol{b} in this parallelogram.
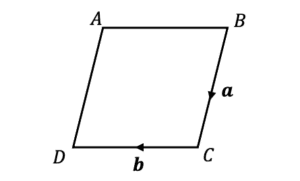
[2 marks]
With vectors, parallel lines of the same length are equal, as they have the same direction and magnitude.
So, in this parallelogram \overrightarrow{AB} is equal to \overrightarrow{DC}, and \overrightarrow{AD} is equal to \overrightarrow{BC}.
So, to find \overrightarrow{AB}…
We know this is the same as \overrightarrow{DC}, which, in this direction, equals \boldsymbol{-b}. So,
\overrightarrow{AB}=\boldsymbol{-b}
And as \overrightarrow{AD} is equal to \overrightarrow{BC},
\overrightarrow{AD}=\boldsymbol{a}
Example 3: Using Ratio
ABC is a triangle.
M lies on the line AB such that AM:MB is 1:1.
Express the vector AM in terms of \boldsymbol{a} and \boldsymbol{b}
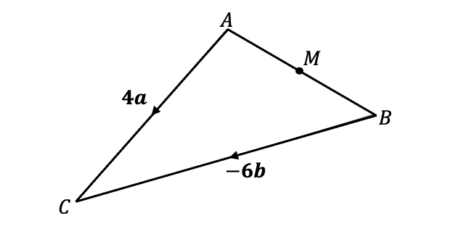
[3 marks]
The ratio 1:1 means M is the midpoint of \overrightarrow{AB}.
Firstly, finding \overrightarrow{AB},
\overrightarrow{AB}=4\boldsymbol{a}+6\boldsymbol{b}
\overrightarrow{AM} is half of \overrightarrow{AB}, so,
\overrightarrow{AM}=\dfrac{1}{2}(4\boldsymbol{a}+6\boldsymbol{b})
\overrightarrow{AM}=2\boldsymbol{a}+3\boldsymbol{b}
Vectors Example Questions
Question 1:
\overrightarrow{AB}=3\boldsymbol{a-b}\\ \overrightarrow{AC}=12\boldsymbol{b}\\ \overrightarrow{AD}=-2\boldsymbol{a-b}
a) Find \overrightarrow{AC}+\overrightarrow{AB}
b) Find 2\times\overrightarrow{AD}
c) Find \overrightarrow{AD}-\overrightarrow{AB}
[6 marks]
a)
\overrightarrow{AC}+\overrightarrow{AB}
=12\boldsymbol{b}+3\boldsymbol{a-b}
=3\boldsymbol{a}+11\boldsymbol{b}
b)
2\times\overrightarrow{AD}
=2\times (-2\boldsymbol{a-b})
=-4\boldsymbol{a}-2\boldsymbol{b}
c)
\overrightarrow{AD}-\overrightarrow{AB}
=-2\boldsymbol{a-b} - (3\boldsymbol{a-b})
=-5\boldsymbol{a}
Question 2: Find the magnitude of vector \begin{pmatrix}12 \\ 16\end{pmatrix}
[3 marks]
Using Pythagoras,
\sqrt{12^2+16^2}=20
Question 3: ABCDEF is a regular hexagon.
Find \overrightarrow{FB} in terms of \boldsymbol{a} and \boldsymbol{b}
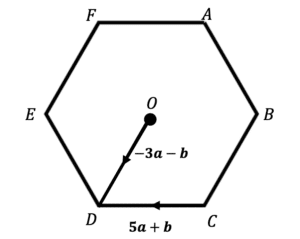
[3 marks]
As this is a regular hexagon, \overrightarrow{FA} and \overrightarrow{DC} are parallel, \overrightarrow{AB} and \overrightarrow{ED} are parallel, and \overrightarrow{EF} and \overrightarrow{CB} are parallel.
To find \overrightarrow{FB}, we need \overrightarrow{FA} plus \overrightarrow{AB}.
\overrightarrow{FA} is the parallel to \overrightarrow{DC}, but in the opposite direction, so,
\overrightarrow{FA}=-5\boldsymbol{a}-\boldsymbol{b}
To find \overrightarrow{AB} , we can start by working out \overrightarrow{OC} which is parallel.
\overrightarrow{OC}=-3\boldsymbol{a}-\boldsymbol{b} -(5\boldsymbol{b}+\boldsymbol{b})=-8\boldsymbol{a}-2\boldsymbol{b}.
Thus,
\overrightarrow{OC}=-8\boldsymbol{a}-2\boldsymbol{b}
So,
\overrightarrow{FB}=-5\boldsymbol{a}-\boldsymbol{b}-8\boldsymbol{a}-2\boldsymbol{b}
\overrightarrow{FB}=-13\boldsymbol{a}-3\boldsymbol{b}
Question 4: M lies on the line \overrightarrow{AC} such that \overrightarrow{AM}:\overrightarrow{MC} is 2:1
Find \overrightarrow{MC} in terms of \boldsymbol{a} and \boldsymbol{b}
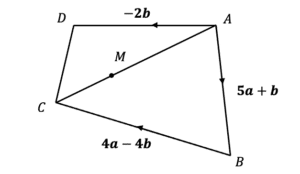
[3 marks]
Let’s firstly find \overrightarrow{AC}
\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}
\overrightarrow{AC}=5\boldsymbol{a}+\boldsymbol{b}+4\boldsymbol{a}-4\boldsymbol{b}
\overrightarrow{AC}=9\boldsymbol{a}-3\boldsymbol{b}
As \overrightarrow{AM}:\overrightarrow{MC} is 2:1, \overrightarrow{MC} is \dfrac{1}{3}\overrightarrow{AC}
\overrightarrow{AC}=\dfrac{1}{3}\times (9\boldsymbol{a}-3\boldsymbol{b})
\overrightarrow{AC}=3\boldsymbol{a}-\boldsymbol{b}
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.