Surface Area of 3D Shapes
Surface Area of 3D Shapes Revision
Surface Area of 3D Shapes
The surface area of a 3D shape is a measure of the total area of all the surfaces of that shape.
When calculating the surface area of 3D shapes, they can fall into one of the following categories:
- All the surfaces are flat – e.g. cube, cuboid, prism
- Some of the surfaces are curved – cylinder, sphere, cone
Surface Area of Cubes and Cuboids
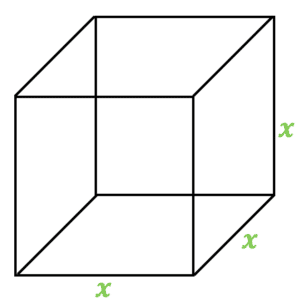
A cube is made of \textcolor{#00d865}{6} identical square faces, i.e. all the dimensions of the cube are the same.
Area of one face : \textcolor{#00d865}{x} \times \textcolor{#00d865}{x} = \textcolor{#00d865}{x^2}
Surface area of a cube :
\boxed{6\textcolor{#00d865}{x^2}}
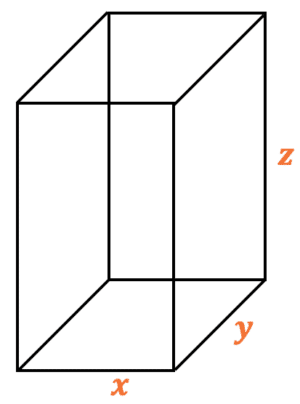
A cuboid is made up of \textcolor{#f95d27}{6} rectangular faces, where the opposite faces are identical, i.e. we have \textcolor{#f95d27}{3} pairs of differently sized rectangles.
Area of the rectangles :
- The first rectangle has sides \textcolor{#f95d27}{x} and \textcolor{#f95d27}{y} \rightarrow \textcolor{#f95d27}{xy}
- The second rectangle has sides \textcolor{#f95d27}{x} and \textcolor{#f95d27}{z} \rightarrow \textcolor{#f95d27}{xz}
- The third rectangle has sides \textcolor{#f95d27}{y} and \textcolor{#f95d27}{z} \rightarrow \textcolor{#f95d27}{yz}
Since there are 2 of each of these rectangles, the total surface area of cuboid is:
\boxed{2(\textcolor{#f95d27}{xy}+\textcolor{#f95d27}{xz}+\textcolor{#f95d27}{yz})}
Surface Area of a Cylinder
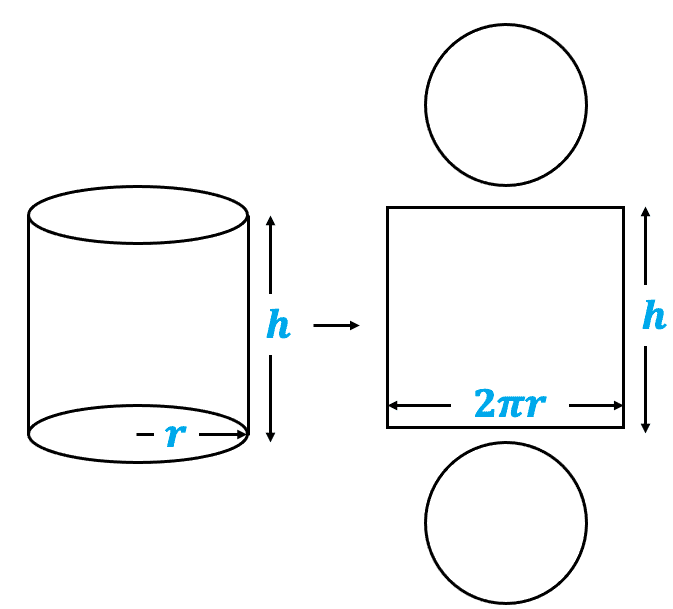
A cylinder is made up of 2 circles and one rectangle, shown in the diagram to the left.
Area of a circle : \textcolor{#10a6f3}{\pi r^2}
Circumference of a circle : \textcolor{#10a6f3}{2 \pi r}
\textcolor{#10a6f3}{r} \rightarrow radius of the circle
Area of rectangle : circumference \times height of cylinder = \textcolor{#10a6f3}{2 \pi rh}
Surface area of a cylinder :
\boxed{\textcolor{#10a6f3}{2 \pi rh} + \textcolor{#10a6f3}{2 \pi r^2}}
Surface Area of a Prism
A prism is a 3D shape that has identical faces at both ends, i.e. the shape has a constant cross-section (shaded faces in the diagram below) in one particular direction. Take a look at the examples below:
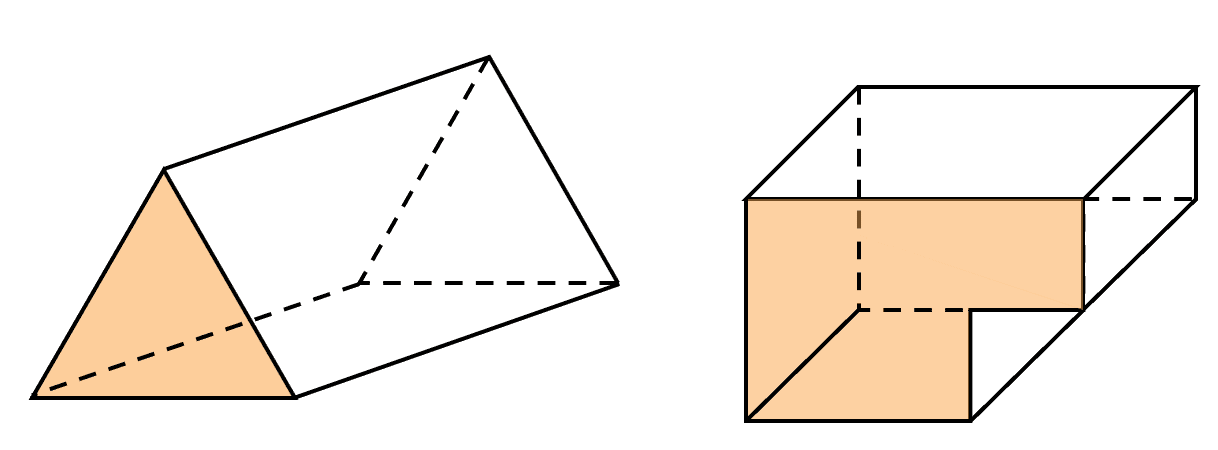
To calculate the area of any prism you need to work out the area of the cross-section and any of the remaining faces.
Reminder: Area of a triangle : \dfrac{1}{2}bh \, Where b \rightarrow base of the triangle and h \rightarrow height of the triangle
Surface area of an (isosceles) triangular prism :
\boxed{\textcolor{#ffad05}{bh} + \textcolor{#ffad05}{2ls} + \textcolor{#ffad05}{bl}}
\textcolor{#ffad05}{l} \rightarrow length of shape
\textcolor{#ffad05}{s} \rightarrow slanted length of triangle
Surface Area of a Cone
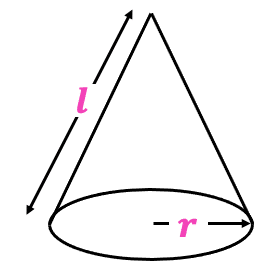
A cone is made up of a circular base and a curved face joining to the circle.
Area of a circle : \textcolor{#f21cc2}{\pi r^2}
Area of the curved face : \textcolor{#f21cc2}{\pi rl}
\textcolor{#f21cc2}{r} \rightarrow radius of the circle
\textcolor{#f21cc2}{l} \rightarrow slanted height of the cone
Surface area of a cone :
\boxed{\textcolor{#f21cc2}{\pi r^2} + \textcolor{#f21cc2}{\pi rl}}
Surface Area of a Sphere
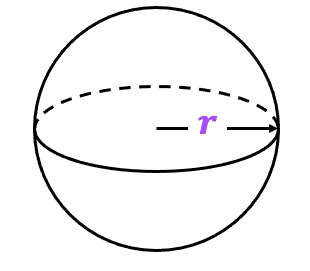
Surface area of a sphere :
\boxed{\textcolor{#aa57ff}{4\pi r^2}}
\textcolor{#aa57ff}{r} \rightarrow radius of the circle
Example 1: Cube and Cuboid
The surface area of cuboid A is 108 \text{ cm}^2
The surface area of cuboid A is twice the size of the surface area of cube B
What is the width of cube B?
[3 marks]
Surface area of cube B = 108 \div 2 = 54 \text{ cm}^2
Let’s say cube B has dimensions x \text{ cm}
Then we have,
6x^2=54
x^2=9
x=3
The width of cube B is 3 \text{ cm}
Example 2: Cylinders
Work out the surface area of a cylinder with radius 3 \text{ cm} and height 10 \text{ cm}
Give your answer in terms of \pi
[2 marks]
Surface area of a cylinder: 2\pi r^2 + 2\pi rh
Substituting r=3 and h=10,
Surface area of a cylinder: 2\pi \times 3^2 + 2\pi \times 3 \times 10 = 78\pi \text{ cm}^2
Example 3: Cone
A cone with radius 4 \text{ cm}, has a surface area of 40\pi \text{ cm}^2
Work out the slanted height of the cone
[3 marks]
Surface area of a cone: \pi r^2 + \pi rl
Substituting r=4,
\pi \times 4^2 + \pi \times 4l = 40\pi
16 \pi + 4l \pi = 40\pi
4l \pi = 24\pi
l = 6
The slanted height of the cone is 6 \text{ cm}.
Example 4: Hemisphere
Shown below is a hemisphere with radius 5 \text{ cm}.
Calculate the surface area of the hemisphere.
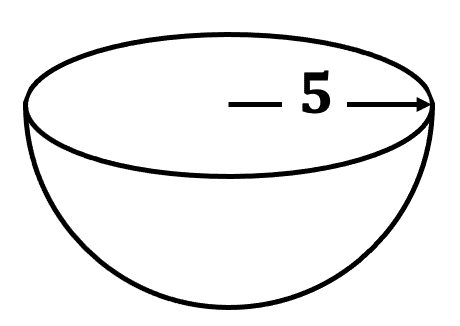
Area of a circle with radius 5 \text{ cm} : \pi \times 5^2 = 25 \pi \text{ cm}^2
Area of a sphere with radius 5 \text{ cm} : 4 \times \pi \times 5^2 = 100 \pi \text{ cm}^2
Area of a hemisphere with radius 5 \text{ cm} : \dfrac{100 \pi}{2} + 25 \pi= 75 \pi \text{ cm}^2
Example 5: Triangular Prism
Work out the surface area of the triangular prism below. Give your answer to two decimal places.
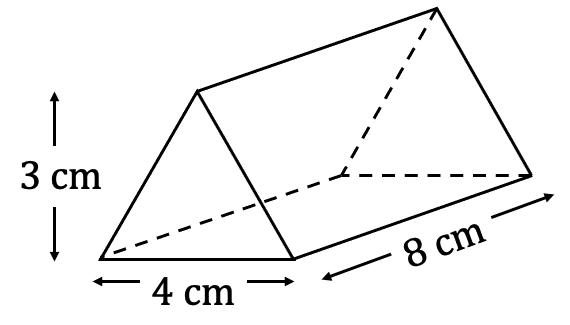
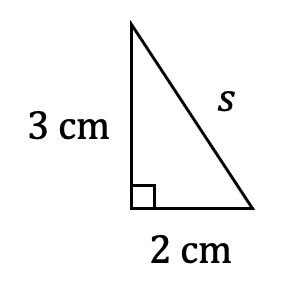
To calculate the area of the two identical rectangles remaining, we first need to calculate the length of the slanted side of the triangle. To do this we use Pythagoras:
s^2=2^2+3^2 = 13
s = \sqrt{13}
Area of the side rectangles : \sqrt{13} \times 8 = 8\sqrt{13} \text{ cm}^2
Surface area of triangular prism : 8\sqrt{13} + 8\sqrt{13} + 32 + 6 + 6 = 44 + 16\sqrt{13} or 101.69 \text{ cm}^2
Surface Area of 3D Shapes Example Questions
Question 1: A cylinder with diameter 12 \text{ cm} has a surface area of 168 \pi \text{ cm}^2.
Work out the height of the cylinder.
[3 marks]
Radius of the cylinder : 6 \text{ cm}
Surface area of a cylinder : 2 \pi rh + 2 \pi r^2
Substituting r=6,
2\pi \times 6^2 + 2\pi \times 6 \times h = 168\pi
72\pi + 12\pi h = 168\pi
12\pi h = 96\pi
h = 8
The height of the cylinder is 8 \text{ cm}
Question 2: 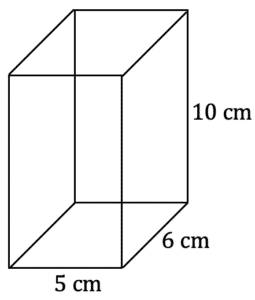
Work out the surface area of the cuboid.
[3 marks]
Surface area of a cuboid : 2(xy+xz+yz)
Substituting x=5 , z=6 and y=10,
2(5\times 10+5\times 6+6\times 10) = 280 \text{ cm}^2Question 3: A sphere has surface area of 36 \pi \text{ cm}^2.
Work out the diameter of the sphere.
[3 marks]
Surface area of a sphere : 4\pi r^2
4\pi r^2=36\pi
r^2=9
r=3
The sphere has a diameter of 6 \text{ cm}
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.