Sets
Sets Revision
Sets
A set is a collection of numbers, usually defined by specific rules or properties. Each object in a set is called an element, or a member.
Introduction
We can use curly brackets to represent sets:
For example, we can represent the set of odd numbers, O, between 1 and 10 as…
O=\{1, 3, 5, 7, 9\}
We can also represent sets in Venn diagrams.
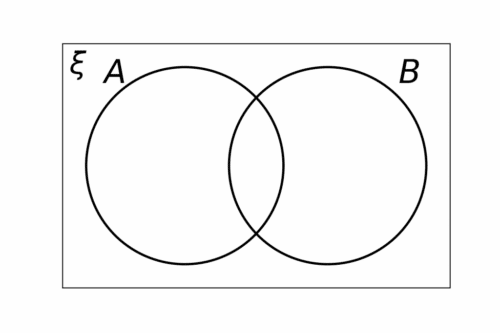
For example, let’s represent the sets A and B in this Venn diagram. A and B both have a circle containing their elements, and the intersection of them contains elements in both A and B.
Any elements outside of the circles do not lie in either set.
Describing Sets
There are some more ways of describing sets:
- The set of numbers, x, such that x is less than 2
\{x:x<2\}
- N(A) means the number of elements. For example, N(A)=12 means there are 12 elements.
The Universal Set and the Empty Set
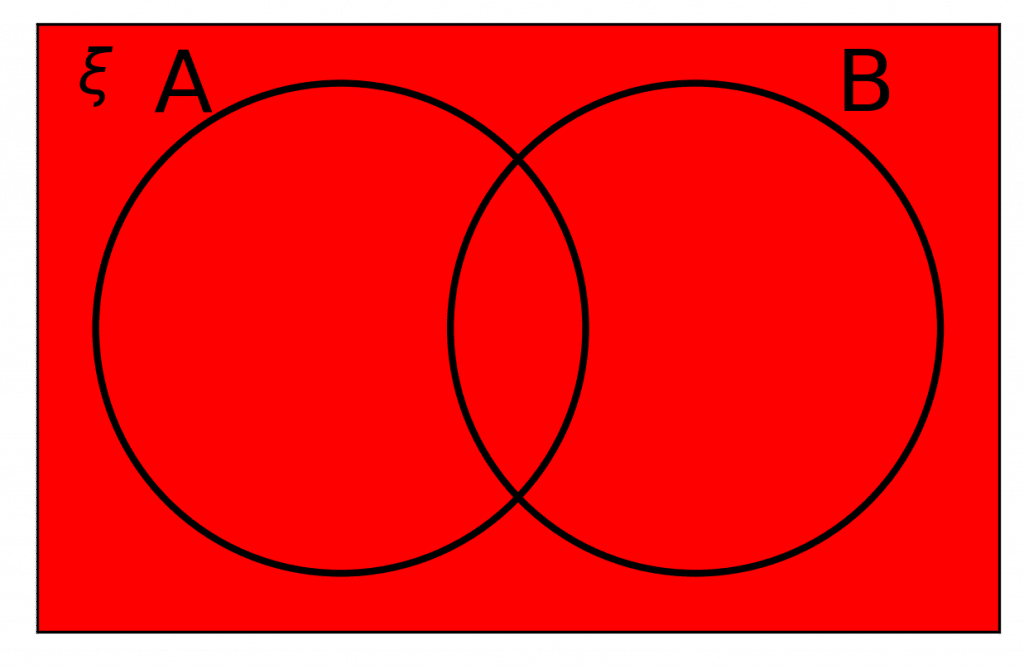
When using a Venn diagram, all elements in the diagram (including those in the circles and outside the circles), are called the universal set. From the universal set, we identify those that fit in A and B.
The universal set is represented by the letter, \xi, which is always present in the top left corner of Venn diagrams.
There is also the empty set, \emptyset, the set containing no elements. The empty set can also be written as the complement of set \xi.
\boldsymbol{A} and \boldsymbol{A'}
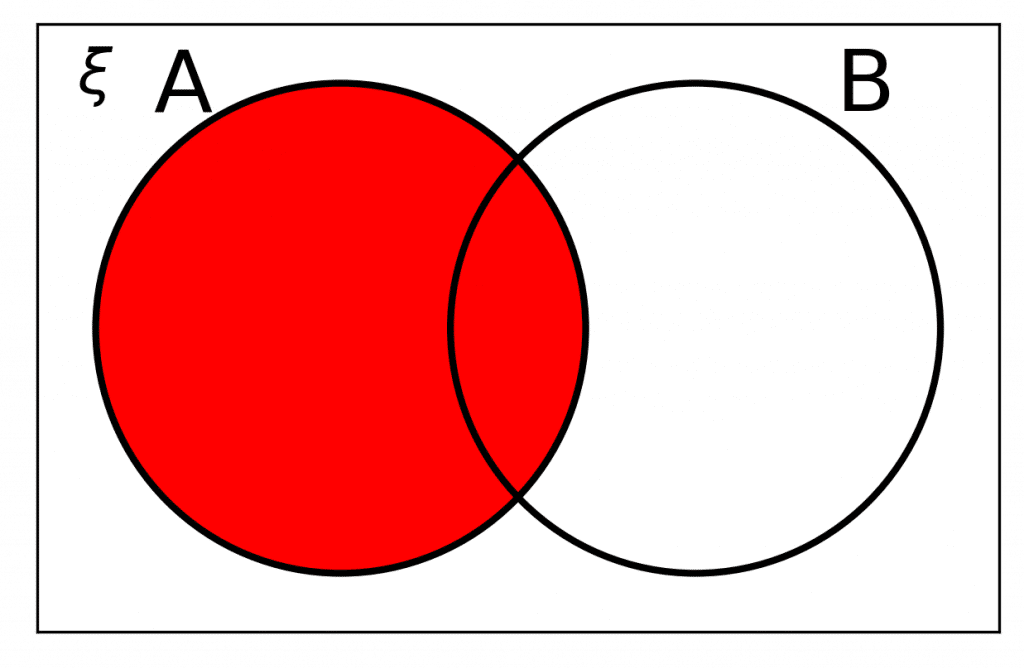
The set A is represented by these sections of the Venn diagram:
This includes the elements only in A and those that are in in both sets A and B
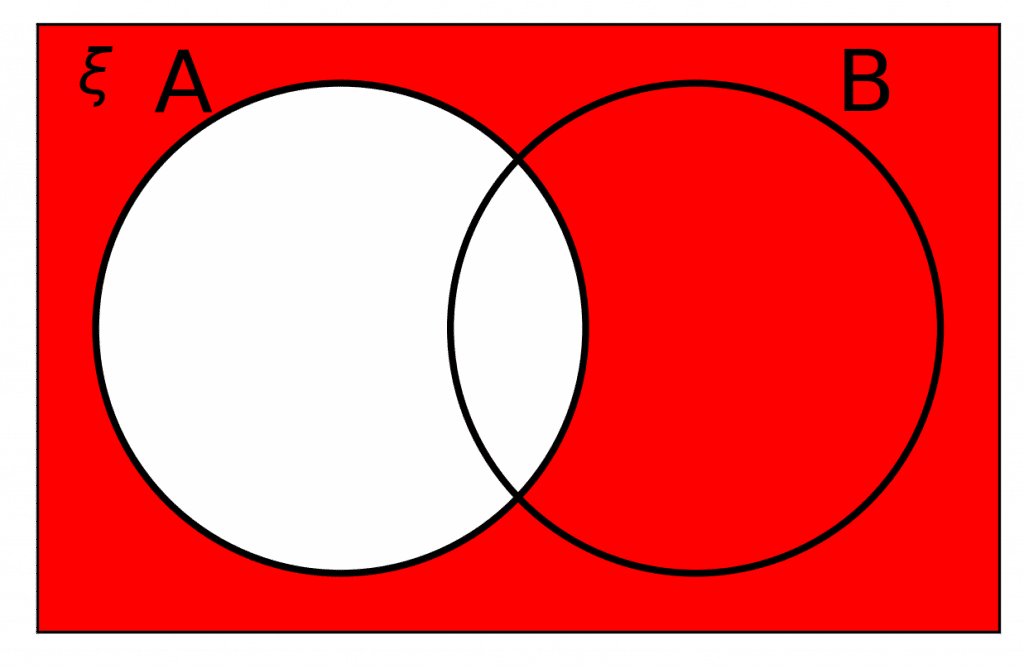
Conversely, A' means NOT in A.
This means, all elements within the the universal set that is not in A, as represented by this Venn diagram:
The Union of Two Sets
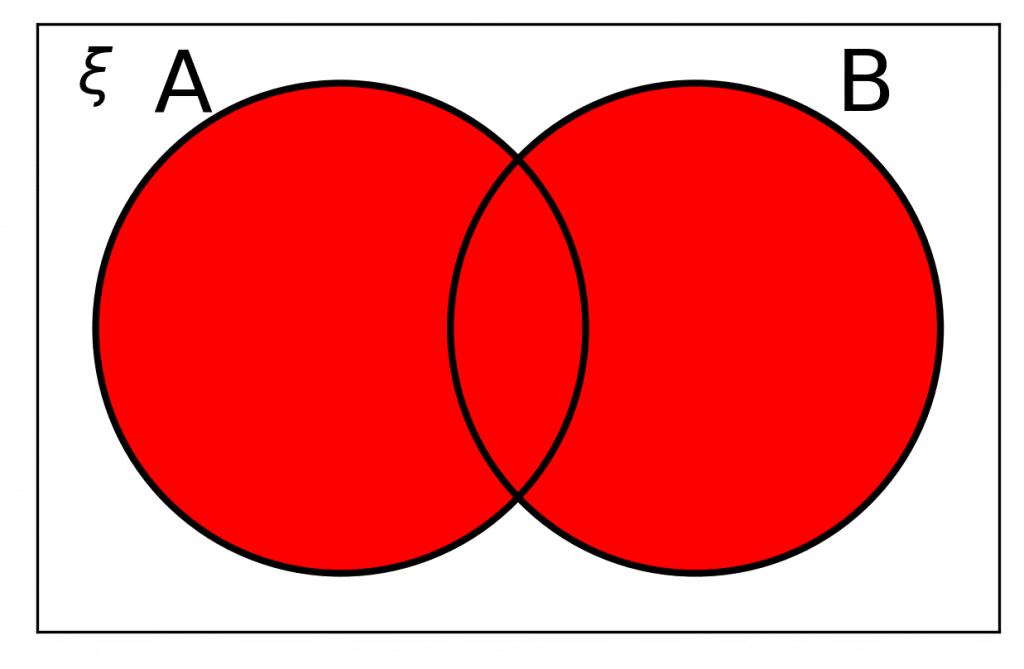
The union of two sets means all elements either in A, B, or both. This can be written as…
A\cup B
The Intersection of Two Sets
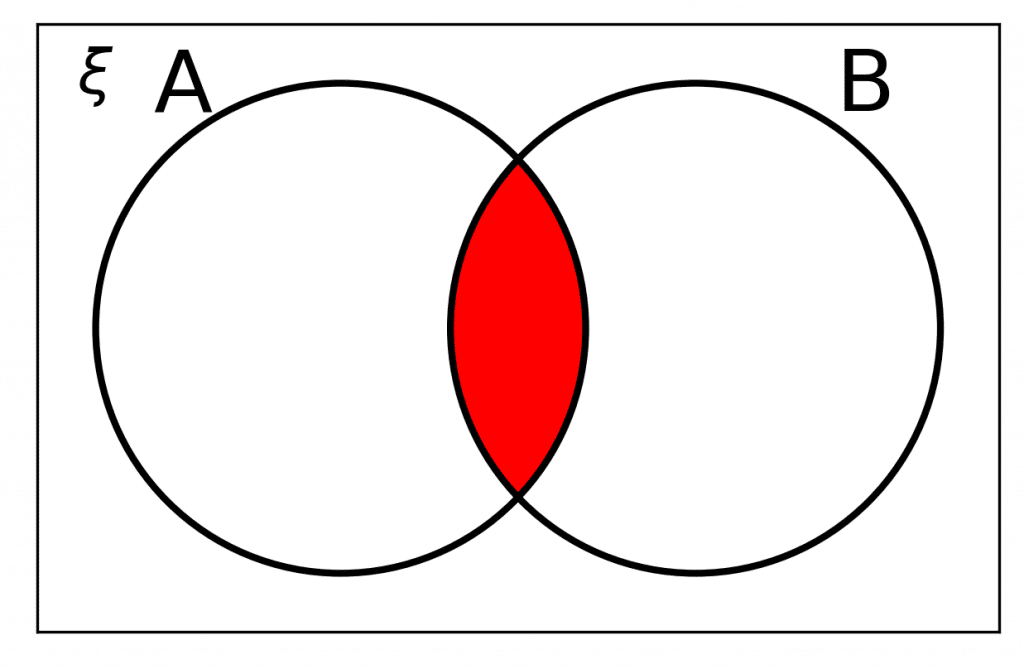
The intersection of two sections contains elements that are in BOTH A and B. This can be written as…
A\cap B
Subsets
A subset is a set that is entirely contained within another set.
For example, if,
A=\{2,6,8\}, and,
B is the set of even numbers between 1 and 10, then,
A \subset B
We use the notation, \not\subset, if a set is not a subset of another set.
Example 1: Sets
A = \{1,4,6,8,10,11\}\\
B=\{2,4,8,10,11,12\}
Write down the sets
a) A\cup B
b) A\cap B
[4 marks]
a) A\cup B means the union of A and B, so all elements in either or both A and B.
So, A\cup B=\{1,2,4,6,8,10,11,12\}
b) A\cap B means the intersection between A and B, so all elements in both A and B.
So, A\cap B=\{4,8,10,11\}
Example 2: Venn Diagrams
Use the following Venn diagram:
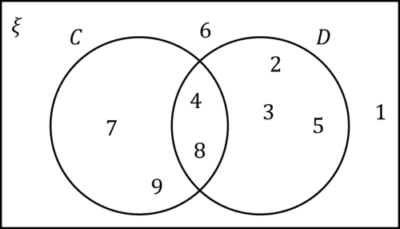
to find,
a) C\cup D
b) C'
[4 marks]
a) C\cup D are the elements that are in either C or D. Therefore,
C\cup D=\{7,9,4,8,2,3,5\}
b) C' are the elements not in C. Therefore,
C'=\{2,3,5,6,1\}
Example 3: Inequalities
Solve the inequality 4x>16, expressing your answer in set notation.
[3 marks]
Let’s solve this inequality as usual,
4x>16
Divide through by 4 to isolate x,
x>4
We can write this in set notation,
\{x:x>4\}
Sets Example Questions
Question 1: X and Y are sets, given by,
X=\{21,26,32,33,38,42,44\}\\
Y=\{11,25,32,34,40,44\}
Find the sets,
a) X\cup Y
b) X\cap Y
[6 marks]
a) The union of X and Y,
X\cup Y=\{11,21,25,26,32,33,34,38,40,42,44\}
b) The intersection of X and Y,
X\cap Y=\{32,44\}Question 2:
Find the sets,
a) C'\cup D'
b) C\cap D'
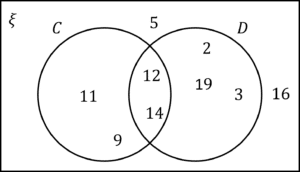
[4 marks]
a) The union of the elements not in C and not in D,
C'\cup D'=\{5,16,11,9,2,3,19\}
b) The intersection between the elements in C but not in D, which is simply the elements in C but not in D,
C\cap D'=\{11,9\}Question 3: Solve the inequality 12x-31<77, giving your solution as a set.
[3 marks]
Let’s solve the inequality as normal,
Add 31 to each side,
12x<108
Divide through by 12,
x<9
As a set,
\{x:x<9\}
Question 4:
X=\{1,3,5,7,9,11,13,15,17,19\}
Decide which set(s) of the following are subset(s) of X,
a) A=\{1,5,8,9\}
b) B=\{7,9,19\}
c) C=\{3,5,13,17\}
[2 marks]
A subset of X will contain only elements that also exist in X
a) Is not a subset as 8 is not in X
B and C are subsets of X as their elements are contained within X.





