Proportion
Proportion Revision
Proportion
Proportion looks at one thing’s size, or one value, and its relationship to another thing’s size, or value.
The two types of proportion we will look at are direct proportion, and inverse proportion, and how to work these out.
Direct Proportion
Direct proportion means as one quantity or value increases, the other increases proportionally. This means, if one quantity doubles, the other also doubles.
Example: Eliza is making cakes. She is following a recipe that says you need 6 eggs to make 18 cakes, but Eliza is going to a bake sale and needs to bring 30 cakes. How many eggs does she need?
The easiest way to work out problems like this, is to see how many eggs Eliza would need per cake:
6\div18=\dfrac{1}{3}
So, if Eliza was going to make one cake, she would need \dfrac{1}{3} of a cake.
But, we want to work out how many eggs she needs for 30 cakes. This is simple now, as we can multiple the amount needed for one cake, by 30,
\dfrac{1}{3}\times30=10 eggs.
Therefore, Eliza would need 10 eggs to make 30 cakes.
Overall method: divide what you know to find the quantity for one unit, and then multiply by the amount you need to find.
Inverse Proportion
You can consider inverse proportion the opposite of direct proportion. When two quantities are inversely proportional, as one increases, the other decreases. So, if one doubles, the other halves.
Example: 6 painters take 54\text{ minutes} to paint a bedroom. How long would it take 12 painters to paint the same bedroom?
So, with 6 people all helping out to paint the room, it takes 54\text{ minutes}, but with 12 painters, there are more people helping, and so the time it takes will decrease.
Similarly to direct proportion, work out how long it would take one person (note: unlike direct proportion where we divide to find one unit, for inverse, we multiply):
6 people = 54\text{ minutes}
1 person =54 \times 6\text{ minutes}= 324\text{ minutes}
So, if it takes one person 324\text{ minutes}, we can divide this time by 12 to work out how long it would take 12 painters, as they would be able to work 12 times as fast:
324\div12=27\text{ minutes}
Therefore, it would take 12 painters 27\text{ minutes} to paint the bedroom.
Overall method: multiply what you know to find the quantity for one unit, and then divide by the amount you need to find.
Direct Proportion with Algebra
We can write x and y are directly proportional as,
y\propto x
Meaning, y is directly proportional to x
This can also be written as,
y=kx
Where k can be called the ‘constant of proportionality’, and it tells us how x and y are related.
Examples:
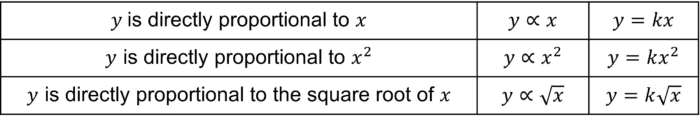
Inverse Proportion with Algebra
We can write x and y are inversely proportional as,
y\propto \dfrac{1}{x}
Meaning, y is inversely proportional to x
This can also be written as,
y=\dfrac{k}{x}
Where k can be called the ‘constant of proportionality’, and it tells us how x and y are related.
Examples:

Graphical Proportion
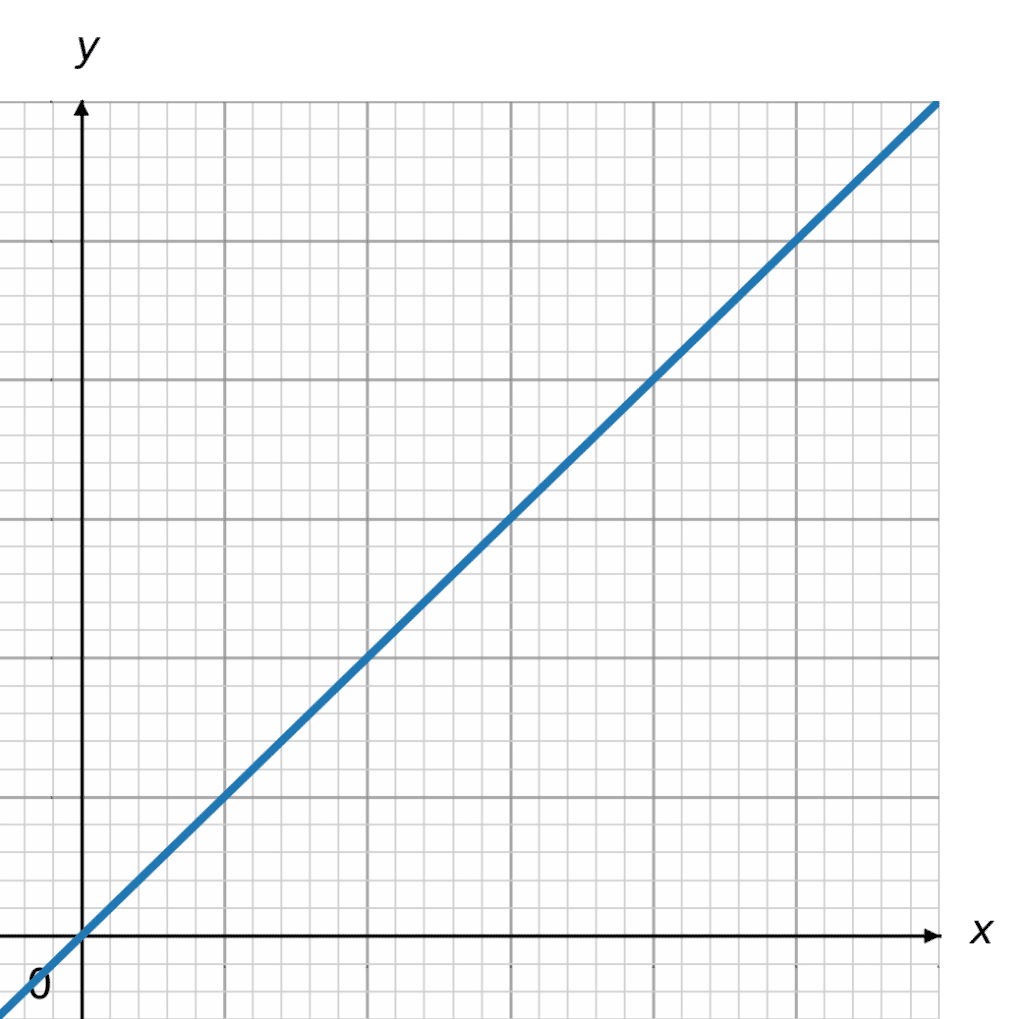
Direct Proportion Graph:
The graph for direct proportion is the graph,
y=kx
or y is directly proportional to x, where k is the ‘constant of proportionality’.
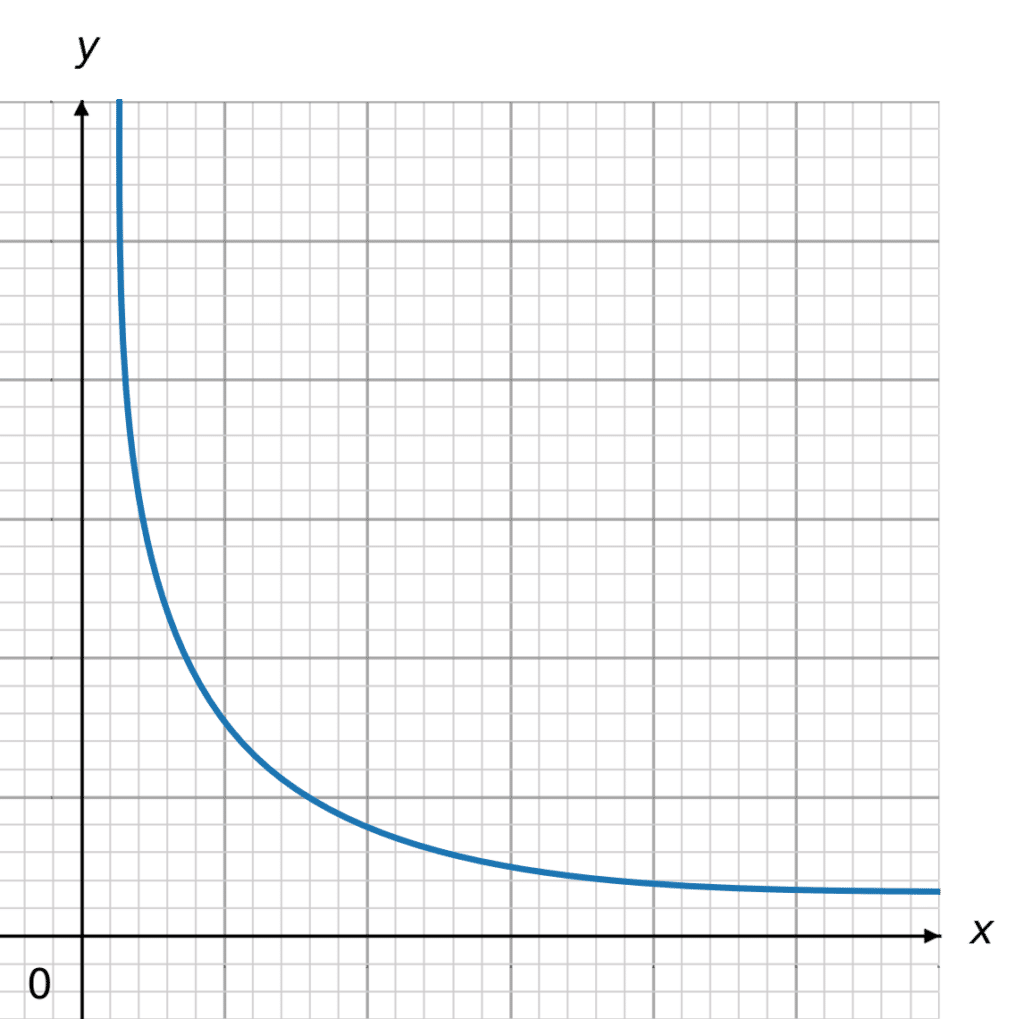
Inverse Proportion Graph:
The graph for inverse proportion is the graph,
y=\dfrac{k}{x}
or y is inversely proportional to x, where k is the ‘constant of proportionality’.
Example 1: Direct Proportion
Sarah is baking some brownies. Here are the ingredients needed to make 6 brownies:

Sarah wants to make 10 brownies. Work out how what quantity of each ingredient Sarah will need.
[3 marks]
We can use what we learnt about direct proportion to work this out:
Overall method: divide what you know to find the quantity for one unit, and then multiply by the amount you need to find.
Let’s start with butter, for one brownie, Sarah would need:
180\text{ g}\div 6=30\text{ g}
So, for 10 brownies:
30\text{ g}\times 10=300\text{ g}
Now the same method for chocolate:
210\text{ g}\div 6=35\text{ g}
35\text{ g}\times 10=350\text{ g}
Flour:
90\text{ g}\div 6=15\text{ g}
15\text{ g}\times 10=150\text{ g}
Eggs:
3\div 6 = 0.5
0.5\times 10 = 5 eggs
Sugar:
270\text{ g}\div 6 = 45\text{ g}
45\text{ g}\times 10=450\text{ g}
So, overall:
300\text{ g} butter
350\text{ g} chocolate
150\text{ g} flour
5 eggs
450\text{ g} sugar
Example 2: Inverse Proportion
Noah and Mike are trying to build a fence, but they have worked out it would take them 8\text{ hours} if they built it on their own, and they want to get it built within 2\text{ hours}.
a) Work out how many people will have to help Noah and Mike to build their fence in 2\text{ hours}.
b) What assumption are you making when answering this question?
[3 marks]
a) We can use the method we learnt about for inverse proportion:
Overall method: multiply what you know to find the quantity for one unit, and then divide by the amount you need to find.
So, if Noah or Mike were building the fence on their own, it would take:
8\text{ hours}\times 2 = 16\text{ hours}
The next stage is to divide this by the number of people helping now, but we do not have this information. Instead, we know we want it to take 2 hours or less. So,
2\text{ hours} = 16\text{ hours}\div\text{number of people}
Which can be rearranged,
\text{Number of people} =16\text{ hours}\div 2\text{ hours}
\text{Number of people}= 8
So, Noah and Mike will need 6 people to help them (to make the total number of people 8).
b) We are assuming that all of the people build the fence at the same rate.
Question 3: Direct Proportion with Algebra
y is directly proportional to the square of x.
When y=27, x=3.
Work out the value of y when x=11
[3 marks]
For this question, we will use the constant of proportionality, k, that we saw earlier.
y is directly proportional to the square of x can be written as,
y\propto x^2
Or,
y=kx^2
We need to first work out what the value of k is in this scenario, using what we know:
When y=12, x=3
So,
27=k(3^2)
27=9k
k=3
Now, we want to work out the value of y when x=11,
y=3(11^2)
y=363
Example 4: Inverse Proportion with Algebra
y is inversely proportional to the square root of x.
When y=1, x=4.
Work out the value of y when x=9
[3 marks]
For this question, we will use the constant of proportionality, k, that we saw earlier.
y is inversely proportional to the square of x can be written as,
y\propto \dfrac{1}{\sqrt{x}}
Or,
y=\dfrac{k}{\sqrt{x}}
We need to first work out what the value of k is in this scenario, using what we know:
When y=1, x=4
So,
1=\dfrac{k}{\sqrt{4}}
2=k
Now, we want to work out the value of y when x=9,
y=\dfrac{2}{\sqrt{9}}
y=\dfrac{2}{3}
Proportion Example Questions
Question 1: Here are the ingredients needed to make 12 pancakes:

Matt is hosting brunch and wants to make 42 pancakes. At home, he has these ingredients:
400\text{ g} flour
8 eggs
1000\text{ ml} milk
10\text{ tbsp} oil
Does Matt have enough to make 42 pancakes?
[3 marks]
We can use direct proportion for this question. Let’s go through each ingredient and see if Matt has enough.
Flour:
108\div12=9\\
9\times42=378\text{ g}
Yes, Matt has enough flour.
Eggs:
2\div12=\dfrac{1}{6}\\
\dfrac{1}{6}\times42=7 eggs
Yes, Matt has enough eggs.
Milk:
300\div12=25\\
25\times42=1050\text{ ml}
Matt does not have enough milk, therefore he cannot make 42 pancakes.
Question 2: It usually takes 6 builders 18 months to complete an extension. One has house a quick deadline, so they hire 27 builders to work on their extension. How long would it take 27 builders if they all work at the same rate?
[3 marks]
Work out how long it would take one builder:
6\times18=108\text{ months}
Divide this by 27 builders:
108\div27=4\text{ months}
Question 3: The cost of a pizza is directly proportional to the square root of the diameter. A pizza with diameter 16\text{ inches} costs £16. Work out how much a pizza with diameter 9\text{ inches} costs.
[4 marks]
A good way to solve this is to form an equation using the constant of proportionality:
y=k\sqrt{x}
Where y is the price of the pizza, and x is the diameter of the pizza.
Let’s sub in y=16, x=16,
16=k\sqrt{16}\\
16=4k\\
k=4
Now, when x=9,
y=4\sqrt{9}\\
y=£12
A 9\text{ inch} pizza costs £12
Question 4: A is inversely proportional to the cube of B.
When A=24, B=2.
Work out the value of A when B=4
[4 marks]
Let’s use an inverse proportion equation:
A=\dfrac{k}{B^3}\\
Let’s sub in what we know,
24=\dfrac{k}{2^3}\\
24=\dfrac{k}{8}\\
k=192
Now, when B=4,
A=\dfrac{192}{4^3}\\
A=\dfrac{192}{64}\\
A=3
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.