Functions
Functions Revision
Functions
A function is an expression that defines a relationship between one independent variable \textcolor{#00d865}{x} and one dependent variable \textcolor{#f95d27}{f(x)}.
The function takes one variable as the input and produces an output. This page explains the following concepts:
- Evaluating Functions
- Composite Functions
- Inverse Functions
Evaluating Functions
We can think of a function as a machine that has an input that is processed by the function to give an output. There are two different types of notations when it comes to writing functions:
- \textcolor{#10a6f3}{f}(\textcolor{#00d865}{x})=\textcolor{#f95d27}{x+2}
- \textcolor{#10a6f3}{f}:\textcolor{#00d865}{x} \longmapsto \textcolor{#f95d27}{x+2}
In both cases x+2 is the function, the \textcolor{#00d865}{x} is the input and the output is the outcome when the input is substituted into the function.
The input can also be seen as the domain – all the values that go into a function.
Note: In certain scenarios, the domain can exclude certain values. For example the following:
- \dfrac{4}{8-2x} \rightarrow x \neq 4: you can’t divide by 0
- \sqrt{6-3x} \rightarrow x \not> 2: you can’t square root a negative number
The output can also be seen as the range – all the values that come out of a function
Let’s say we have the function
\textcolor{#10a6f3}{f}(\textcolor{#00d865}{x})=\textcolor{#f95d27}{2x+7} or \textcolor{#10a6f3}{f}:\textcolor{#00d865}{x} \longmapsto \textcolor{#f95d27}{2x+7}
We want to evaluate \textcolor{#10a6f3}{f}(\textcolor{#00d865}{2}) or \textcolor{#10a6f3}{f}:\textcolor{#00d865}{2}, to do this we substitute x=2
\textcolor{#10a6f3}{f}(\textcolor{#00d865}{2})=\textcolor{#f95d27}{2(}\textcolor{#00d865}{2}\textcolor{#f95d27}{)+7=11} or \textcolor{#10a6f3}{f}:\textcolor{#00d865}{2} \longmapsto \textcolor{#f95d27}{2(}\textcolor{#00d865}{2}\textcolor{#f95d27}{)+7=11}
Mapping Between Two Sets
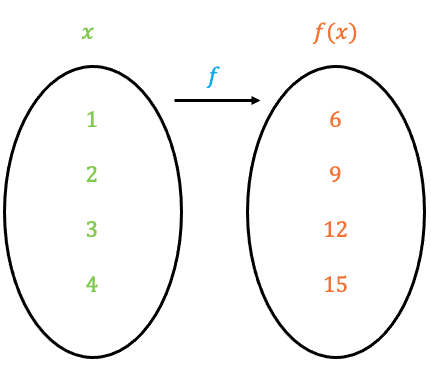
Let’s say we have the set,
\textcolor{#00d865}{x} \in \{1, 2, 3, 4\}
And the function,
\textcolor{#10a6f3}{f}(\textcolor{#00d865}{x})=\textcolor{#f95d27}{3(x+1)}
Then to calculate the mapping of set \textcolor{#00d865}{x} when using the function \textcolor{#10a6f3}{f(x)}, we need to calculate the following:
\textcolor{#10a6f3}{f}(\textcolor{#00d865}{1})=\textcolor{#f95d27}{3(}\textcolor{#00d865}{1}\textcolor{#f95d27}{+1)=6}
\textcolor{#10a6f3}{f}(\textcolor{#00d865}{2})=\textcolor{#f95d27}{3(}\textcolor{#00d865}{2}\textcolor{#f95d27}{+1)=9}
\textcolor{#10a6f3}{f}(\textcolor{#00d865}{3})=\textcolor{#f95d27}{3(}\textcolor{#00d865}{3}\textcolor{#f95d27}{+1)=12}
\textcolor{#10a6f3}{f}(\textcolor{#00d865}{4})=\textcolor{#f95d27}{3(}\textcolor{#00d865}{4}\textcolor{#f95d27}{+1)=15}
The domain is \{1, 2, 3, 4\}
The range is \{6, 9, 12, 15\}
Inverse Functions
The inverse function \textcolor{#10a6f3}{f^{-1}} undoes the process of the function \textcolor{#10a6f3}{f}. In other words, the inverse of a function tells us how to get from the output of a function to the input.
Let’s say we have a function that has a process of:
‘adds 1‘ \rightarrow f(x)=x+1
Then the reverse of this would be the process of:
‘subtracts 1‘ \rightarrow f^{-1}(x)=x-1
Example: Find the inverse of the function f(x)=2x+1
Step 1: Write the equation in the form x = f(y)
For this we need to replace all the x‘s in the equation with y‘s and set the equation equal to x
f(x)=2x+1 \rightarrow x=2y+1
Step 2: Rearrange the above equation to make y the subject
x=2y+1 \rightarrow y=\dfrac{x-1}{2}
Step 3: Replace y with f^{-1}(x)
y=\dfrac{x-1}{2} \rightarrow f^{-1}(x)=\dfrac{x-1}{2}
Let’s say for this particular function we use the set \textcolor{#00d865}{x} \in \{1, 2, 3, 4\} as our input (domain). Then the output (range), would be:
f(\textcolor{#00d865}{1})=2(\textcolor{#00d865}{1})+1=\textcolor{#f95d27}{3}
f(\textcolor{#00d865}{2})=2(\textcolor{#00d865}{2})+1=\textcolor{#f95d27}{5}
f(\textcolor{#00d865}{3})=2(\textcolor{#00d865}{3})+1=\textcolor{#f95d27}{7}
f(\textcolor{#00d865}{4})=2(\textcolor{#00d865}{4})+1=\textcolor{#f95d27}{9}
Now using the inverse function \textcolor{#10a6f3}{f^{-1}=\dfrac{x-1}{2}}, we can use the output values we just calculated to get back to the input:
f^{-1}(\textcolor{#f95d27}{3})=\dfrac{\textcolor{#f95d27}{3}-1}{2}=\textcolor{#00d865}{1}
f^{-1}(\textcolor{#f95d27}{5})=\dfrac{\textcolor{#f95d27}{5}-1}{2}=\textcolor{#00d865}{2}
f^{-1}(\textcolor{#f95d27}{7})=\dfrac{\textcolor{#f95d27}{7}-1}{2}=\textcolor{#00d865}{3}
f^{-1}(\textcolor{#f95d27}{9})=\dfrac{\textcolor{#f95d27}{9}-1}{2}=\textcolor{#00d865}{4}
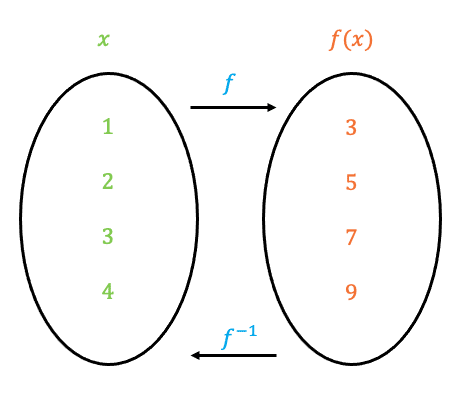
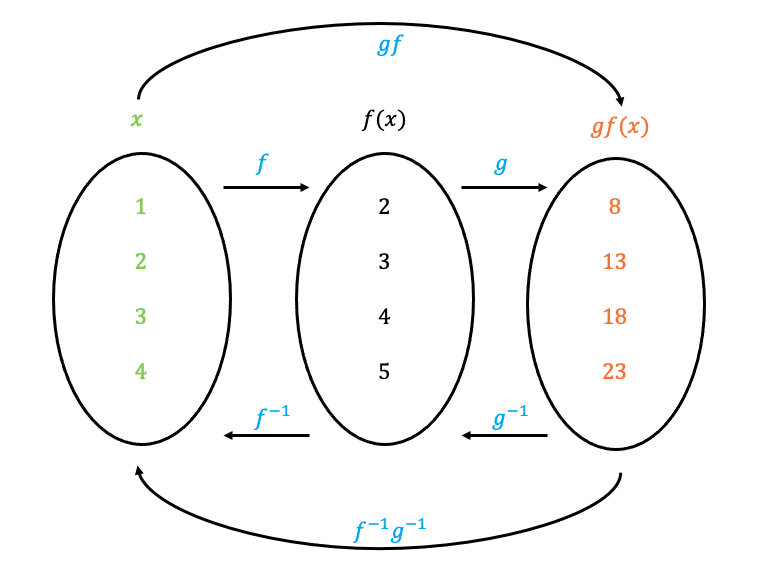
Composite Functions
A composite function is when the output of one function \textcolor{#10a6f3}{f} is used as the input of another function \textcolor{#10a6f3}{g}.
Example: f(x)=x+1 and g(x)=5x-2
- gf(x): means substituting f(x) into g(x)
Let’s say the domain of this particular problem is \textcolor{#00d865}{x} \in \{1, 2, 3, 4\}
The range would be the values of:
gf(1)=5(1)+3=8
gf(2)=5(2)+3=13
gf(3)=5(3)+3=18
gf(4)=5(4)+3=23
The diagram below demonstrates this composite function. We can calculate the output directly, which is what we did above. However you can calculate the functions individually, this will be demonstrated further down. To ‘undo’ the functions we can calculate the inverse of gf(x) or calculate the inverses individually.
- fg(x): means substituting g(x) into f(x)
- ff(x): means substituting f(x) into itself
Let’s say we wanted to calculate ff(1), we have two approaches to answering this question which both gets you to the same answer.
- Calculate f(1)=1+1=2, then f(f(1))=f(2)=2+1=3
- Calculate f(f(x))=f(x+1)=(x+1)+1=x+2, then f(f(1))=1+2=3
Note: Since the inverse of f, is the reverse process of the function f, when you apply them together in a composite function you get back to the input:
ff^{-1}(x)=x
Example 1: Evaluating Functions
Let f(x)=x^2+4
a) Find f(3)
[1 mark]
f(3)=(3)^2+4=13
b) Solve f(x)=20
[2 marks]
x^2+4=20 \rightarrow x^2=16 \rightarrow x=\pm 4
Example 2: Composite Functions
Let f(x)=(x+1)^2 and g(x)=3x+5
a) Find fg(3)
[2 marks]
fg(3)=f(g(3))=f(3(3)+5)=f(14)=(14+1)^2=225
b) Solve gf(x)=32
[3 marks]
gf(x)=g((x+1)^2)=3(x+1)^2+5=3x^2+6x+8
3x^2+6x+8=32 \rightarrow 3x^2+6x-24=0
Dividing this quadratic through by 3: x^2+2x-8=0
Factorising: (x+4)(x-2)=0 \rightarrow x=-4, x=2
Example 3: Inverse Functions
Let f(x)=\dfrac{x+5}{3}
a) Solve f^{-1}(x)=10
[3 marks]
x=\dfrac{y+5}{3} \rightarrow y=3x-5
f^{-1}(x)=3x-5
3x-5=10 \rightarrow 3x=15 \rightarrow x=5
Alternative Approach: As we know f^{-1}(x)=10 then x=f(10)=\dfrac{10+5}{3}=5
b) Find f^{-1}(15)
[1 mark]
Using our answer to part a) f^{-1}(x)=3x-5
f^{-1}(15)=3(15)-5=40
Functions Example Questions
Question 1:
Let f(x)=5x+2
a) Find f(2)
[1 mark]
b) Solve f(x)=22
[2 marks]
a) f(2)=5(2)+2=12
b) 5x+2=22 \rightarrow 5x=20 \rightarrow x=4
Question 2: Let f(x)=2x^2+6 and g(x)=\dfrac{x}{4}
a) Find fg(4)
[2 marks]
b) Solve gf(x)=2
[3 marks]
a) fg(4)=f(g(4))=f\left(\dfrac{4}{4}\right)=f(1)=2(1)^2+6=8
b) gf(x)=g\left(\dfrac{x}{4}\right)=\dfrac{2x^2+6}{4}
\dfrac{2x^2+6}{4}=2 \rightarrow 2x^2+6=8\rightarrow 2x^2=2\rightarrow x^2=1\rightarrow x=\pm 1
Question 3: Let f(x)=\sqrt{x+5}
a) Solve f^{-1}(x)=4
[3 marks]
b) Find f^{-1}(4)
[1 mark]
a) x=\sqrt{y+5} \rightarrow y=x^2-5
f^{-1}(x)=x^2-5
x^2-5=4 \rightarrow x^2=9 \rightarrow x=\pm 3
Alternative Approach: As we know f^{-1}(x)=4 then x=f(4)=\sqrt{4+5}=\pm 3
b) Using our answer to part a) f^{-1}(x)=x^2-5
f^{-1}(4)=4^2-5=11
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.