Expressions and Equations
Expressions and Equations Revision
Expressions and Equations
Expressions and equations use numbers to represent words and letters, making complicated problems easier to understand and solve.
Expressions: algebraic statements which may consist of numbers, letters, and operations, but do not contain equals signs. For example x+1
Equations: uses an equals sign to equate an equation to something. For example x+1=4
Substitution
Substitution means replacing letters or symbols in algebraic equations/expressions with numbers.
For example, in the equation
a = 2b + 5
We can use substitution to replace the letters to use this equation. We could find the value of a when b=2 by using substitution, for example:
a=2\times2 +5
We need to remember BIDMAS when computing this (division/multiplication come before addition/subtraction):
a = 4+5\\
a=9
We can also use substitution to replace words in equations too (these are often formulae):
\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}
We could work out speed when distance = 3\text{ km} and time = 0.5\text{ hours},
\text{Speed}=\dfrac{3}{0.5}
\text{Speed}=6\text{km/h}
Substitution – Harder
Sometimes, we may have to use substitution in more difficult equations or expressions, but it works in the same way.
For example, equations may have quite a few variables:
y = 2a + a + 4b -12c + 16c -2d + 4
You may notice there are multiples of some of the variables, for example, it contains 2a and a. Therefore, we will need to collect like terms before substituting:
2a + a = 3a
-12c+16c=4c
So, the simplified equation is,
y = 3a+4b+4c-2d+4
Now we can use substitution:
With more complicated equations like this, it is even more important to remember BIDMAS. It is often helpful to use brackets to make it easier to substitute into complicated equations.
For example, work out y given,
a=2\\ b=5\\ c=3\\ d=1\\
Remember that a(b)=a\times b,
y = 3(2)+4(5)+4(3)-2(1)+4
y=6+20+12-2+4
y=40
Forming Expressions
When forming an expression, we will often use an algebraic variable (usually a letter like x, y, a, b, but can be any letter) to represent an unknown.
- For example, Sophie has some sweets, and she buys 3 more sweets at the shop. Represent the number of sweets Sophie has using an algebraic expression:
We do not know how many sweets Sophie started with, so we can use a variable to represent this. As we are not told which variable to use, we can choose any letter, let’s choose s.
Sophie has s sweets and buys 3 more, so overall Sophie has:
s + 3 sweets.
Expressions can be more complicated, where there is more than one unknown.
- Sophie, Chloe, and Ella have some sweets. Represent the total number of sweets as an expression.
Here, we have 3 unknowns, so we need 3 algebraic symbols. We will call the number of sweets Sophie has s, the number of sweets Chloe has c, and for Ella e:
s + c + e
Forming Equations
Similarly, when forming equations we often use an algebraic variable (usually a letter like x, y, a, b, but can be any letter) to represent an unknown.
- For example, Sophie has some sweets, and she loses 3 of them. Sophie now has y sweets. Represent y in an equation:
We do not know how many sweets Sophie started with, so we can use s.
Sophie has s sweets and loses 3, resulting in her having y sweets. We can represent this as:
s - 3 = y sweets.
Forming Equations – Harder
Equations can be more complicated, for example:
- Sophie and Ella each have some lollipops. Their friend Chloe has 2 times the amount of lollipops Sophie has. In total, they have 30 lollipops. Represent this as an equation.
We can call the number of sweets Sophie has s and the number Ella has e. If Chloe has double the amount of sweets Sophie has, we can call this 2s:
s + 2s + e = 30
As we have 2 separate lots of s here, we can group the s‘s together:
3s+e=30
Example 1: Expressions
Barney has 3 siblings. His youngest sister Joy is half of his age, his brother Jason is 6 years older than Barney, and his older sister Daisy is 4 years older than Jason. By representing Joy’s age as x, write expressions to represent the age of each siblings in terms of x.
[4 marks]
Joy: x
Barney is double the age of Joy: 2x
Jason is 6 years older than Barney: 2x+6
Daisy is 4 years older than Jason: 2x+6+4 = 2x+10
Example 2: Equations
The total length of all of the sides of this 2D shape is 100. Represent this as an equation.
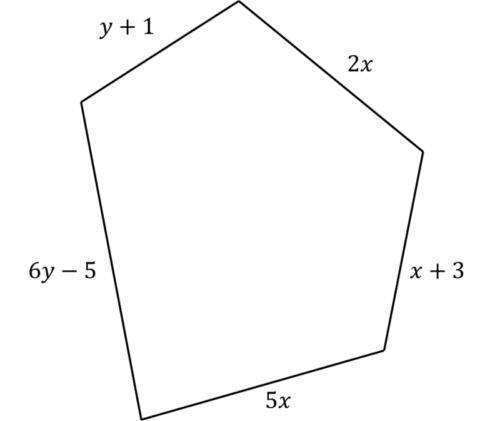
[4 marks]
To find the total length, we add all the the sides together:
2x+x+3+5x+6y-5+y+1=100
We can collect the x‘s, the y‘s and the numbers to simplify this equation:
8x+7y-1=100
We can now add 1 to each side:
8x+7y=101
Expressions and Equations Example Questions
Question 1: Tesni is buying food for a picnic. She buys 6 pizzas for £x each, 12 packets of crisps for £y each, and 10 sausage rolls for £z each. Write an expression for the total amount Tesni spends.
[3 marks]
6 pizzas for £x each: 6x
12 packets of crisps for £y each: 12y
10 sausage rolls for £z each: 10z
Total: 6x + 12y+10z
Question 2: Theo, Harry, Emerson and William are hosting a party. 35 people are attending. Theo invited x people and Harry invited y people. Emerson invited double the amount of people Theo invited, and William invited 5 less people than Theo.
Represent the number of people at the party with an equation in terms of x.
[3 marks]
Theo: x
Harry: y
Emerson: 2x
William:2x-5
Total:
x+y+2x+2x-5=35\\
y+5x-5=35\\
y+5x=40
Question 3:
K=6l + 3m -\dfrac{n}{3}\\
l = 2\\
m = 4\\
n = 12
Work out the value of K
[3 marks]
Using substitution,
K=6(2)+3(4)-\dfrac{12}{3}\\ K=12+12-4\\ K=20You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.