Revise
Differentiation with Linear Kinematics
Differentiation with Linear Kinematics Revision
Differentiation with Linear Kinematics
Kinematics looks at the motion of a particle, considering displacement, velocity, and acceleration. We can model the movement of anything as a particle, such as a car or a ball.
Make sure you are happy with the following topic before continuing:
Displacement
Displacement is slightly different to distance…
We know distance is a measurement that is always positive – you cannot get a negative distance.
Displacement however, measures the distance from a fixed point of origin, and if this distance is forwards from the origin, the displacement is positive, and if it is backwards, the displacement is negative. We call displacement s, and it is usually measured in \text{m}.
For example, both the distance and displacement of the following ball from the origin is 4:
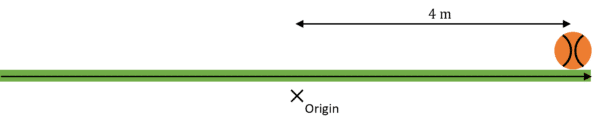
However, in the following example, while the distance is 3, the displacement is -3:
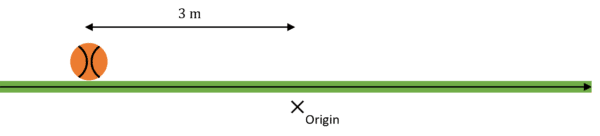
Velocity
Velocity measures a change of displacement, or how quickly the displacement is changing.
Velocity is usually written v, and measured in \text{m/s}. We can look at it in a similar way to displacement:
Velocity is slightly different to speed, as it also takes direction into consideration. If v = 4, then the particle is moving in the positive direction with a speed of 4 \text{m/s}. If v = -4, then the particle is moving in the negative direction with a speed of 4 \text{m/s}.
Acceleration
Acceleration measures a change of velocity, or how quickly the velocity is changing.
Acceleration is usually written a, and measured in \text{m/s}^2.
If a = 3, the particle is accelerating at 3\text{ m/s}^2.
If a = -3, the particle is decelerating at 3\text{ m/s}^2.
Using Differentiation
We can use differentiation to help us find displacement, velocity, and acceleration…
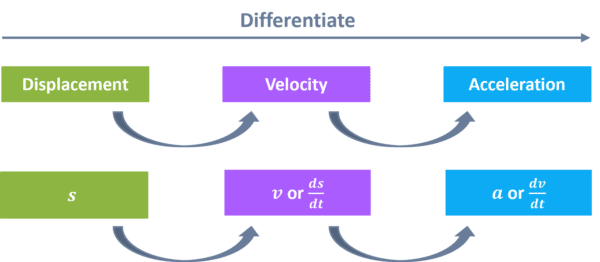
We express displacement, velocity, and acceleration in terms of t, which is time, usually in seconds.
If we differentiate an expression for displacement, we would get an expression for velocity, and if we differentiate an expression for velocity, we would get an expression for acceleration.
Example 1: Using Differentiation
The displacement of a car is shown in the following expression:
s = 6t^3 + 5t^2 + 11t -4
Find an expression for the velocity and acceleration of this car.
[4 marks]
To find velocity, we differentiate once:
s = 6t^3 + 5t^2 + 11t -4\\
\dfrac{\text{d}s}{\text{d}t} = 18t^2 + 10t + 11
To find acceleration, we differentiate the velocity:
v = 18t^2 + 10t + 11\\
\dfrac{\text{d}v}{\text{d}t} = 36t + 10
Example 2: Applied Differentiation
A ball is moving along a straight line. The displacement of the particle, from fixed origin point O, at time, t seconds is:
s = 7t^2 - 5t - 12
a) Find the particle’s initial distance from O
b) Find t when the particle is at rest
[5 marks]
a) ‘Initial’ means t=0, so we can use t=0 in the displacement equation to find the initial distance:
s = 7t^2 - 5t - 12\\
s = 7(0)^2 - 5(0) - 12\\
s = -12
The initial displacement is -12, however, the question is asking for distance, so this is 12\text{ m}.
b) When the particle is at rest, the velocity will be 0\text{ m/s}^2, so we need to firstly differentiate to find the expression for velocity.
s = 7t^2 - 5t - 12\\
\dfrac{\text{d}s}{\text{d}t} = 14t - 5\\
Now we can sub in \dfrac{ds}{dt}=0\text{ m/s}^2
0 = 14t - 5\\
14t = 5\\
t = \dfrac{5}{14}\text{ s}
Differentiation with Linear Kinematics Example Questions
Question 1: The velocity of a particle is given by the expression
v = 21t^2 + 5t - 11
Find an expression for the acceleration of the particle.
[2 marks]
We need to differentiate the velocity to find the acceleration:
v = 21t^2 + 5t - 11\\
\dfrac{\text{d}v}{\text{d}t} = 42t + 5
Question 1: The displacement of a train is given by the expression
s = 7t^2 - 14t + 6
Find the velocity and acceleration of the train at t = 2\text{ s}.
[4 marks]
Differentiate to find an expression for velocity:
s = 7t^2 - 14t + 6\\
\dfrac{\text{d}s}{\text{d}t} = 14t - 14
When t = 2\text{ s}, the velocity is:
v = 14(2) - 14\\
v = 14\text{ m/s}
Differentiate to find an expression for acceleration:
v = 14t - 14\\
\dfrac{\text{d}v}{\text{d}t} = 14
At t=2\text{ s}, the acceleration is 14\text{ m/s}^2
Question 3: The displacement of a particle is given by the expression
s = 3t^2 + 12t - 2
Work out whether the acceleration of this particle remains constant or is variable with time.
[4 marks]
Let’s find an expression for the acceleration:
s = 3t^2 + 12t - 2\\
\dfrac{\text{d}s}{\text{d}t} = 6t+12\\
\dfrac{\text{d}v}{\text{d}t} = 6
So, the acceleration is 6\text{ m/s}^2.
As there is no t in the equation for acceleration, we know it will not change if t changes, and so will always remain constant at 6\text{ m/s}^2.
