Differentiation with Graphs
Differentiation with Graphs Revision
Differentiation with Graphs
Differentiation allows us to find the variable rate of change, so when looking at a graph, differentiation gives us the gradient at any given point.
Make sure you are happy with the following topic before continuing:
Gradients of Lines
The following graph shows the line y = 2x + 1
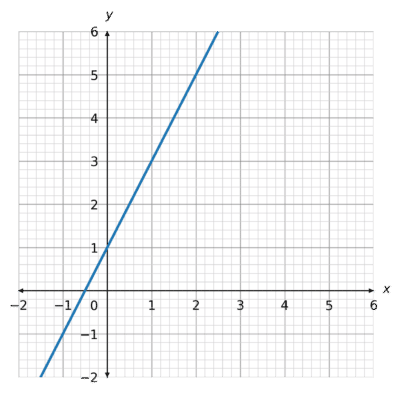
We know to find the gradient we can find 2 coordinates on the line and calculate \dfrac{\text{change in} y}{\text{change in} x}:
Using (0,1) and (3, 7):
\dfrac{7-1}{3-0} = 2So, the gradient, or rate of change, of this line is 2.
We could also calculate this by differentiating the equation of the line:
y = 2x + 1\\\dfrac{\text{d}y}{\text{d}x}=1\times 2x^{1-1} + 0 = 2
Gradients of Curves
We can also use differentiation to find the gradients of curves at given points.
The following graph shows the curve y = x^2 + 2
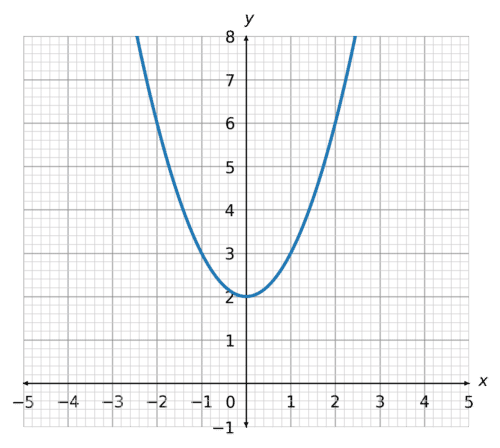
Curves have many gradients, depending on which point you are looking at.
For example:
Find the gradient of the curve y = x^2 + 2 at the point (2,6).
Differentiate:
\dfrac{\text{d}y}{\text{d}x} = 2xSub in the value of x from (2,6):
\dfrac{\text{d}y}{\text{d}x} = 2(2) = 4Therefore, the gradient at the point (2,6) is 4.
If we were asked the same question but with the point (4, 18), we would substitute x=4 into the derivative:
\dfrac{\text{d}y}{\text{d}x} = 2(4) = 8
Stationary Points
A stationary point on a curve occurs when the gradient is 0.
The curve below has 2 stationary points, one that is a maximum point, and one that is a minimum point.
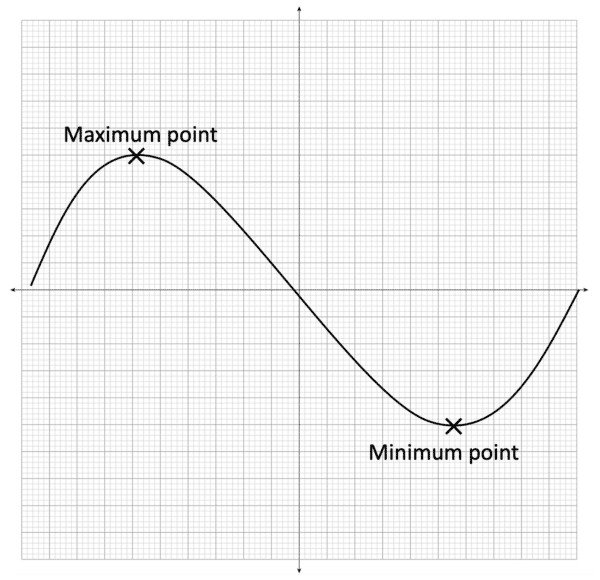
The gradient at both the maximum and minimum point is 0.
Finding the Coordinates of Stationary points:
For example, if a curve had the equation y = 2x^2 + 4, we can use differentiation to find the coordinates of the stationary point(s).
\dfrac{\text{d}y}{\text{d}x} = 4x
At a stationary point, we know the gradient, 4x is 0:
4x = 0\\
We solve this equation:
x = 0
Therefore, the stationary point occurs when x=0. To find the full coordinate, we can sub this x coordinate back into the curve’s equation:
y = 2(0^2) + 4 = 4
Coordinate: (0,4)
Example 1: Gradients of Lines
Find the gradients of the 3 lines on this graph:
[3 marks]
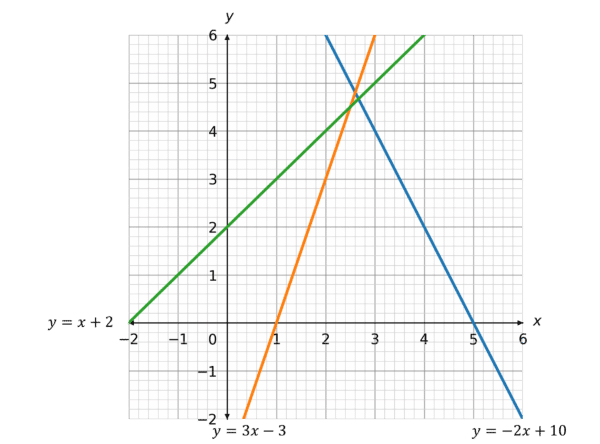
y = 3x - 3\\ \dfrac{\text{d}y}{\text{d}x} = 3
y = x + 2\\
\dfrac{\text{d}y}{\text{d}x} = 1
Example 2: Stationary Points
Find the coordinates of the stationary point of the following curve, y = 3x^2+12x+1, deciding whether this is a minimum or maximum point.
[4 marks]
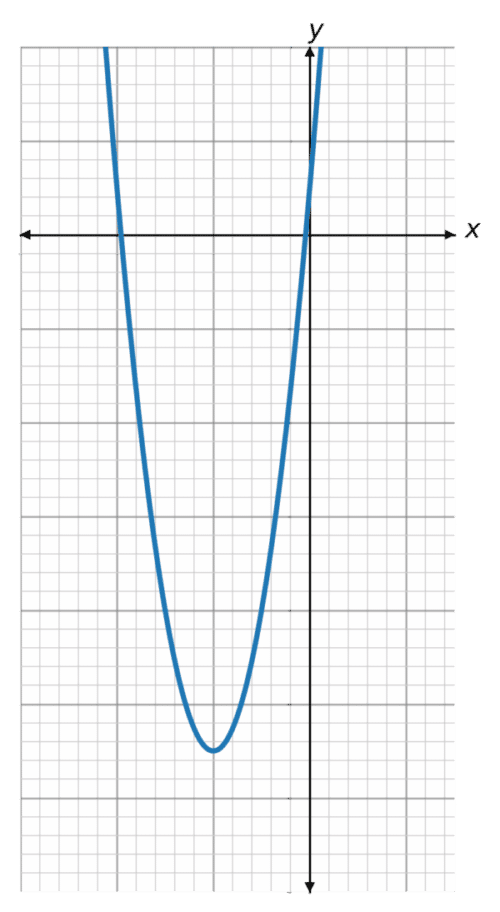
We can differentiate to find the gradient:
y=3x^2+12x+1\\ \dfrac{\text{d}y}{\text{d}x}=6x+12
At the stationary point, the gradient will be 0.
\dfrac{\text{d}y}{\text{d}x}=6x+12=0\\ 6x=-12\\ x=-2
Sub this into the equation to find the y coordinate:
y=3(-2)^2+12(-2)+1\\ y=-11
Coordinate: (-2,11)
We can see from the graph that this is a minimum point, as the curve decreases to this point, and then increases after.
Differentiation with Graphs Example Questions
Question 1: Find the gradient of the line y=4x+3
[2 marks]
Differentiate:
\dfrac{\text{d}y}{\text{d}x}=4The gradient of the line is 4.
Question 2: The graph below shows the curve y=-x^2+4x+6.
Find the coordinate of the stationary point, stating whether this is a minimum or maximum point.
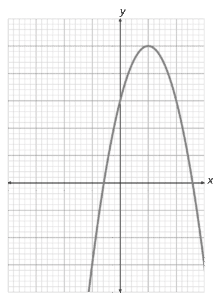
[3 marks]
Differentiate:
\dfrac{\text{d}y}{\text{d}x}=-2x+4
Stationary point occurs when the gradient is 0:
-2x+4=0\\ 2x=4\\ x=2\\Sub x into the curve equation:
y=-(2)^2+4(2)+6
y =10
(2,10)
This is a maximum point.
Question 3: Find the coordinates of the 2 stationary points of the curve y=\dfrac{1}{3}x^3+2x^2+3x+1
[5 marks]
Differentiate:
\dfrac{\text{d}y}{\text{d}x} = x^2+4x+3
Gradient will be 0 at the stationary points, so:
x^2+4x+3=0\\ (x+3)(x+1)=0\\x=-3 and x=-1
When x=-3,
y=\dfrac{1}{3}(-3)^3+2(-3)^2+3(-3)+1 =1Stationary point: (-3, 1)
When x=-1,
y=\dfrac{1}{3}(-1)^3+2(-1)^2+3(-1)+1 =-\dfrac{1}{3}Stationary point: \left(-1, -\dfrac{1}{3}\right)
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.