Construction
Construction Revision
Construction
Constructions are accurate drawings/diagrams of lines, angles, and shapes. You will need a pencil, rules, pair of compasses, and a protractor for this topic.
Make sure you are happy with the following topics before continuing:
Lines
The first construction we will look at is lines. You need to be able to measure and draw lines to the nearest millimeter.
A millimeter is a tenth of a \text{cm} and as they are such a small measurement, it is important to try and be as accurate as possible whilst using a ruler.
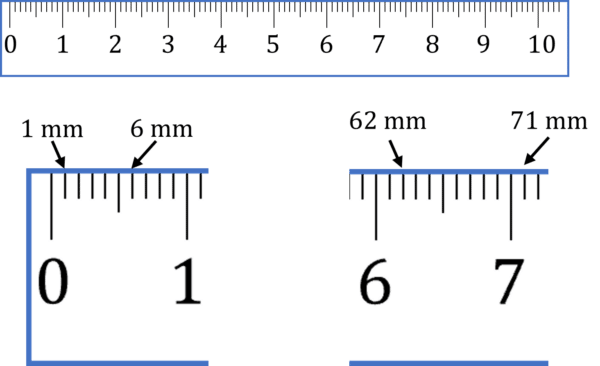
You may be asked to draw a line using a ruler.
For example – construct a 79\text{ mm} straight line:

Triangles
You may need to construct a triangle, or other 2D shape, from the lengths of the sides using a pair of compasses and a ruler.
For example – construct a triangle ABC with the following side lengths:
AB = 6\text{ cm}\\ AC = 3\text{ cm}\\ BC = 5\text{ cm}
Step \textbf{1}: To draw line AB, measure 6\text{ cm} on a ruler and draw a line this length.

Step \textbf{2}: To measure line AC, set your pair of compasses at 3\text{ cm} and draw an arc with A as the center.
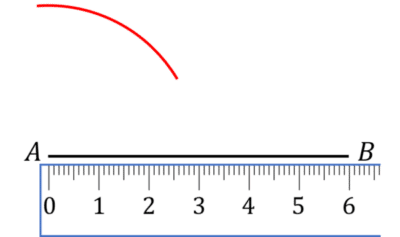
Step \textbf{3}: To measure line BC, set your pair of compasses at 5\text{ cm} and draw an arc with B as the center.
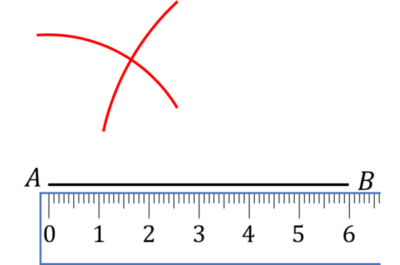
Step \textbf{4}: Draw a line joining A with the intersection of the 2 arcs, and repeat for B.
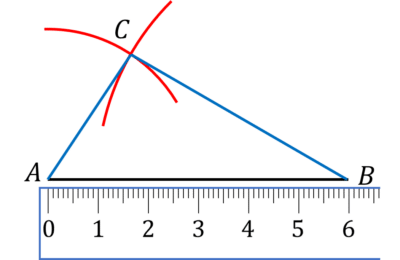
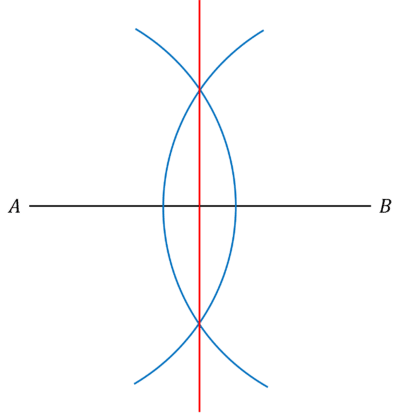
Perpendicular Bisector
You may need to construct a perpendicular bisector of a straight line using a pair of compasses and a ruler.
For example, using a pair of compasses and a ruler, find the perpendicular bisector of the line AB.

Step \textbf{1}: Set your compasses to over half the length AB and place at the point A. Draw an arc.

Step \textbf{2}: Repeat the same from point B, making sure your pair of compasses is set at the same length.

Step \textbf{3}: Draw a line passing though the two points where the arcs cross. This is the perpendicular bisector.
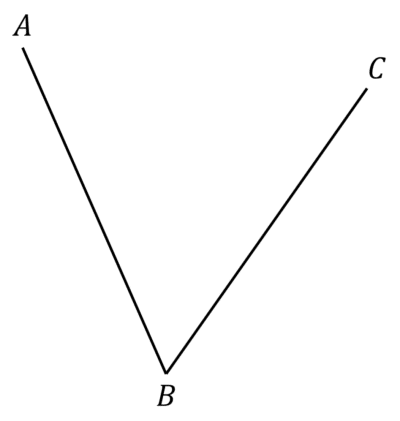
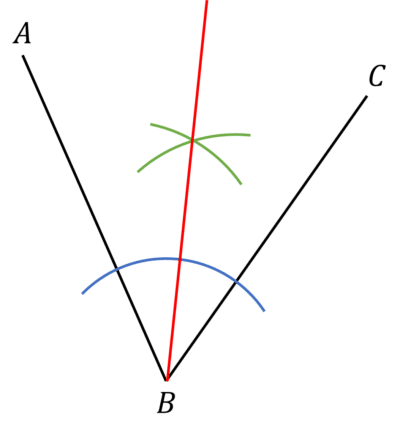
Angle Bisector
You may need to construct an angle bisector. This is a line precisely splitting an angle in two.
For example, construct a line, equidistant from line AB and BC.
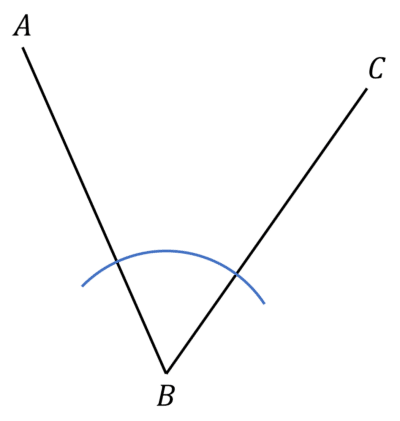
Step \textbf{1}: Place the point of your pair off compasses at B and draw a small arc, crossing both AB and BC.
Step \textbf{2}: Place the point of your pair off compasses where the arc crosses AB and draw an arc between the lines AB and BC. Repeat with your compasses at the point the arc crosses BC and draw another arc, keeping your compasses the same length, and making sure the arcs cross over.
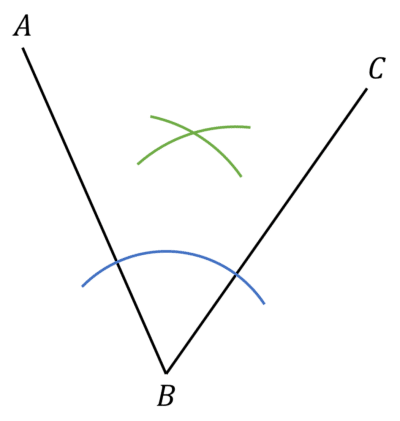
Step \textbf{2}: Draw a line from B passing through the point the arcs cross. This is the angle bisector.
Construction Example Questions
Question 1: Below are 4 centimetre rulers. Which of this options correctly represents a line of 95\text{ mm}?
a)

b)

c)

d)

[2 marks]
c is correct as the line starts at the 0 mark and ends at 9.5\text{ cm}
Question 2: Which of the following options correctly shows the first step to bisecting an angle?
a) 
b) 
c) 
d) 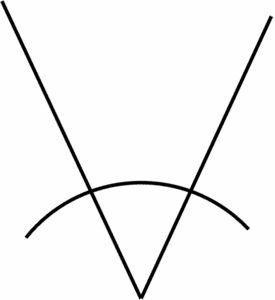
[2 marks]
d is the correct first step to bisecting an angle.
Question 2: Select the option that correctly shows the first 2 steps of drawing a triangle with the following length sides:
AB: 5\text{ cm} AC: 2\text{cm} BC: 4\text{ cm}
a) 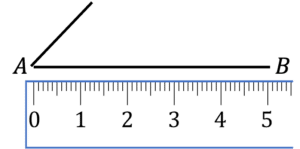
b) 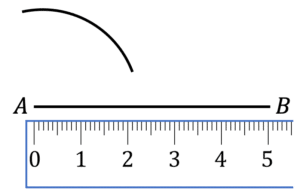
c) 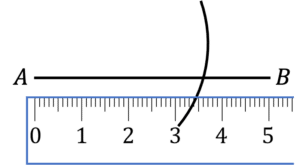
d) 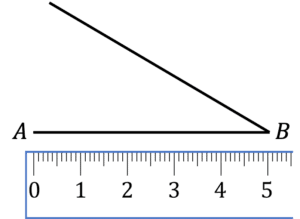
[2 marks]
b is the correct first 2 steps to drawing the triangle.







