Revise
Congruence
Congruence Revision
Congruence
For two shapes to be congruent, they must be the same shape and the same size. Congruent shapes may be mirror images of each other.
It is important to note that this is different from shapes being similar, as similar shapes can be different sizes, but must be the same shape.
Basic Congruence
If two or more shapes have the same length sides and the same angles, they are congruent to each other, or they have congruence.
For example, all of these rectangles are congruent as the all have sides 12\text{ cm} and 3\text{ cm}, and right angles.
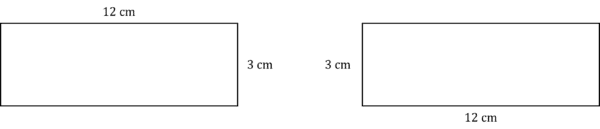
Congruence can also remain when a shape is transformed by either a rotation, a reflection, or a translation. This is because these transformations preserve length and angle, so the shapes still have the same shape and size.
Note: congruence does not remain when a shape is enlarged, as the size of the shape changes.
All of these shapes are congruent:
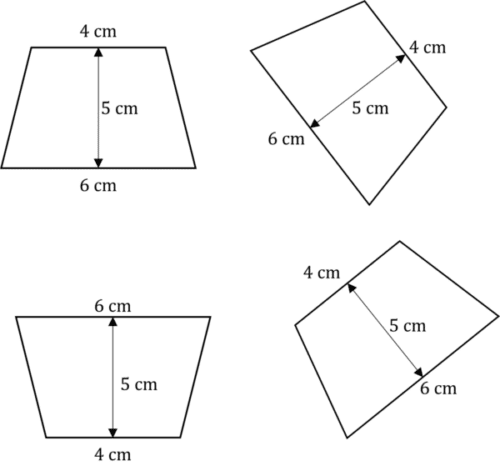
Congruence of Triangles
You can tell if triangles are congruent without knowing the length of every side or the size of every angle.
You can decide if two triangles are congruent if…
1. SSS (side side side): 3 sides are the same length
In all cases, if two triangles have 3 sides the same length, in any order, the triangles are congruent.
For example, these triangles are congruent,
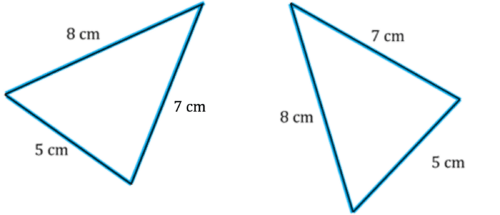
2. AAS (angle angle side): 2 angles and a side are the same
In all cases, if two triangles have two angles and any one side the same, they are congruent.
For example, these triangles are congruent,
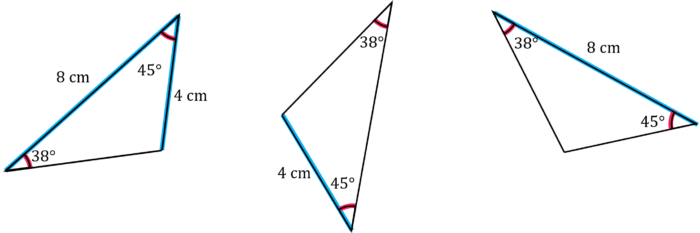
3. SAS (side angle side): 2 sides and the angle between them are the same
In all cases, if two triangles have two sides of equal length with an angle of the same size between them, they are congruent.
For example, these triangles are congruent,
4. RHS (right-angle, hypotenuse, side): in two right angle triangles, the hypotenuse and one other side will be equal
In all cases, the right angle, the longest side (the hypotenuse) and either of the other sides must be equal in two triangles for them to be congruent.
For example, these triangles are congruent,
Example 1: Basic Congruence
Which two of the following shapes are congruent?
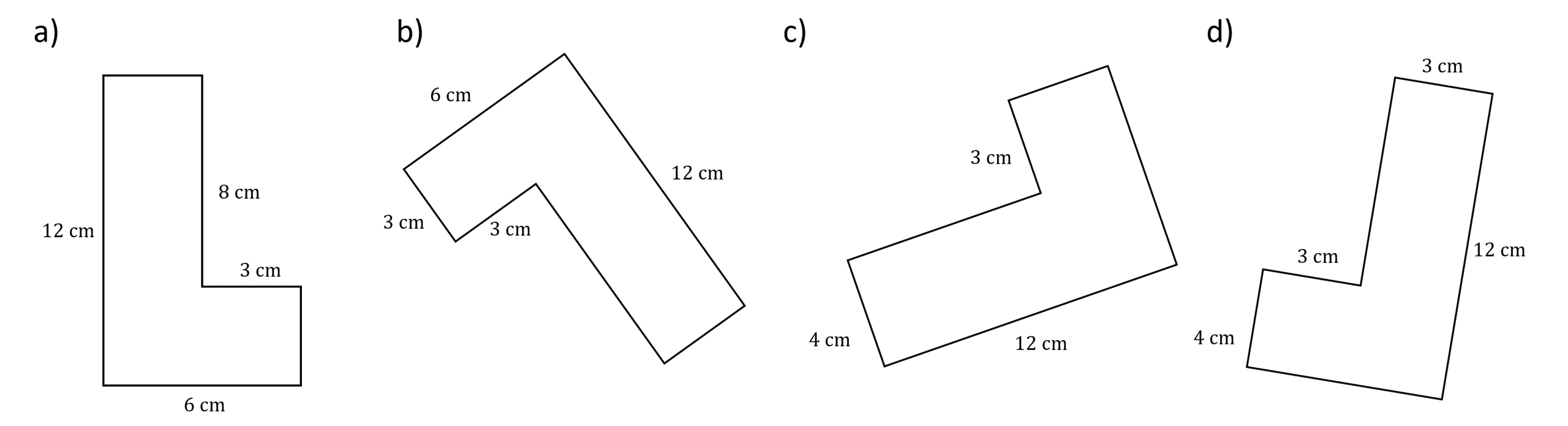
[2 marks]
As these shapes all look quite similar, it is important to look at the side lengths to decide which are congruent, rather than just guessing by observation. We do not need to worry about angles for this as they all contain only right angles.
Let’s look side by side.
Longest side: they each have a longest side of length 12\text{ cm}
Top of L shape: for a), we can work out the top of the L is length 3\text{ cm}, which is the same as b) and d). We can ignore c) going forward as it definitely is not congruent.
So we now need to decide which of a), b) and d) are congruent.
It is clear c) and d) are not congruent as they have equivalent sides with measurements 3 and 4.
By doing 12-8=4 on a), it is clear a) and d) are congruent.
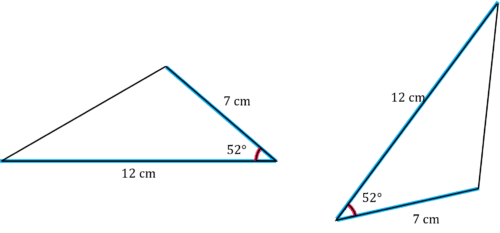
Example 2: Congruence of Triangles
Which option shows a triangle congruent to the one above?
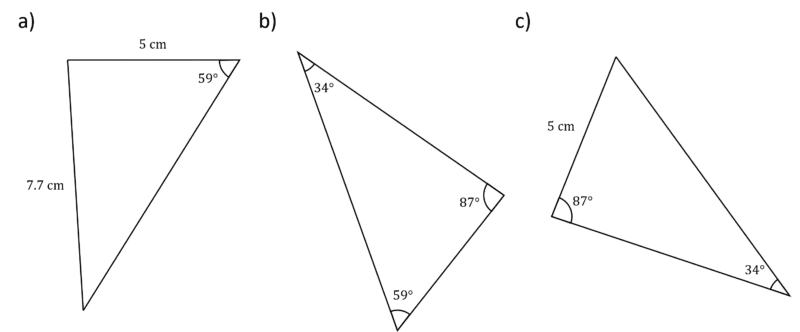
[2 marks]
Let’s look at each option:
a) Is not congruent as for SAS to work, the angle must be between the two sides.
b) Could be congruent but we do not have enough information so cannot prove congruence by having three of the same angles.
c) This is congruent by AAS.
Congruence Example Questions
Question 1: Identify the pair of congruent shapes from the options below.
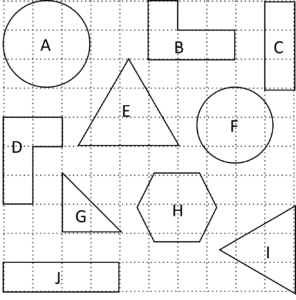
[2 marks]
If B was rotated 90\degree clockwise, it would be shape D. Hence, B and D are congruent.
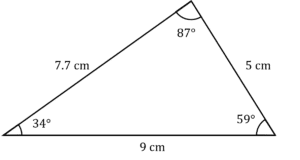
Question 2: All of the following triangles are congruent.
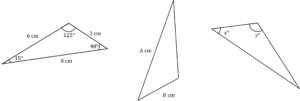
Work out the values of A, B, x and y.
[2 marks]
As the triangles are all congruent, the angles and sides will be the same.
By looking at the triangles we can identify:
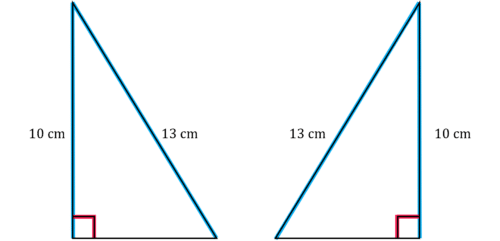
A=8\\ B=3\\ x=40\\ y=125\\Question 3: Identify which pair of these triangles are congruent:
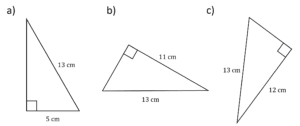
[3 marks]
All of these triangles have different lengths, so it is impossible to tell which are congruent. This is because the RHS rule relies on having two sides the same length and a right angle.
In order to decide, we will use Pythagoras’ Theorem to find the missing sides of each shape:
a) 13^2-5^2=144\\
\sqrt{144}=12
b) 13^2-11^2=48\\
\sqrt{48}=4\sqrt{3}
c) 13^2-12^2=25\\
\sqrt{25}=5
Therefore, a) and c) are congruent by the RHS rule.
