Circle Theorems
Circle Theorems Revision
Circle Theorems
Circle theorems are rules used when finding angles and lengths within a circle or parts connected to a circle.
There are 9 theorems you will need to understand and be able to use.
Rule 1
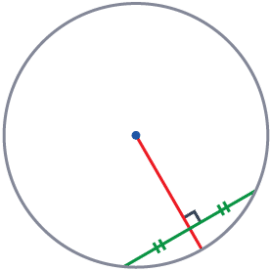
Perpendicular Bisector of a Chord
A chord is any line drawn from one point on the circumference to another.
The perpendicular bisector of a chord ALWAYS passes through the centre of the circle.
Rule 2
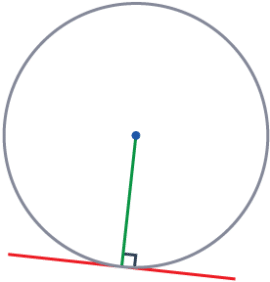
Angle between a Radius and Tangent
A tangent to a circle will always meet a radius – as the radius can go from the centre of the circle to anywhere on the circumference.
A tangent and a radius will ALWAYS meet at 90\degree
Rule 3
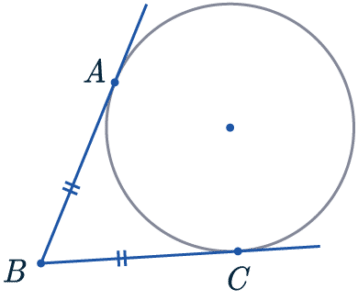
Tangents from the Same Point
As there can be multiple tangents to the same point, two tangents can come from the same point and meet the circle at 2 separate points.
Tangents from the same point to the circle are the same length.
Rule 4
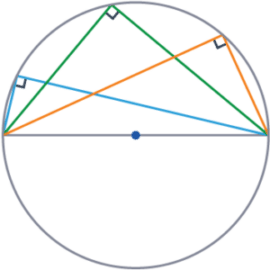
Angles in a Semi-Circle
When an angle extends from a diameter, this can be described as the diameter subtends an angle at the circumference.
The angle subtended from the diameter within a semi-circle is 90\degree
Rule 5
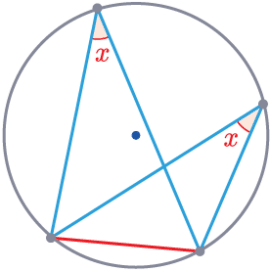
Angle in the Same Segment
When a chord is drawn in a circle, both sides of the chord are segments.
When triangles are drawn from the chord in the same segment, the angles at the circumference are equal.
Rule 6

Angle at the Centre
This rule occurs when an angle at the centre and an angle at the circumference are subtended from the same two points on the circumference.
The angle at the centre of the circle is double the size of the angle at the circumference.
Rule 7
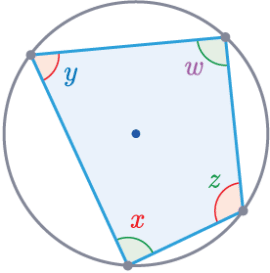
Cyclic Quadrilaterals
A cyclic quadrilateral is a four-sided shape, where each vertex touches the circumference of a circle.
In a cyclic quadrilateral, opposite angles ALWAYS add to 180\degree
\textcolor{purple}{w}+\textcolor{red}{x}=180\degree
\textcolor{blue}{y}+\textcolor{limegreen}{z}=180\degree
Rule 8
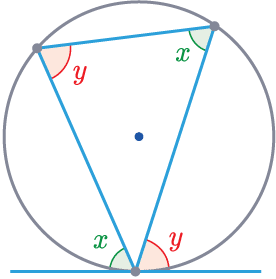
Alternate Segment Theory
This rule is relevant where there is a triangle within a circle with a tangent to the circle at one of the points.
The angle between the tangent and the side of the triangle is equal to the opposite angle of the triangle.
Rule 9
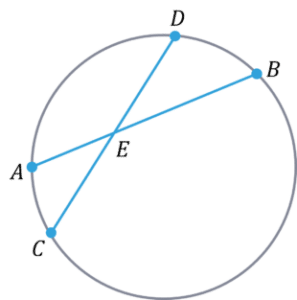
Intersecting chords
This rule is made of 2 properties surrounding chords.
1. Internal Intersection
For any two chords that insect within a circle:
AE\times EB=CE\times ED
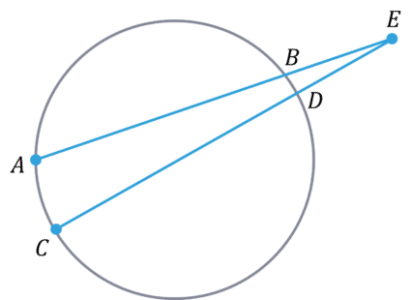
2. External Intersection
For any two chords are extended and meet outside a circle:
AE\times BE=CE\times DE
Example 1: Using Circle Theorems
Use one of the circle theorems to work out the length BC, given that the length AB is 7.5\text{ cm}
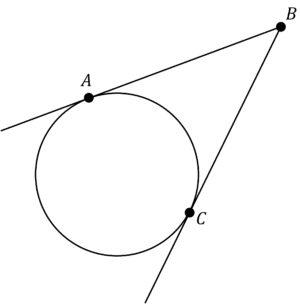
[1 mark]
This is a simple question as we can quickly apply only one rule: rule 3.
As these tangents come from the same point, there is the same length between each of the lines meeting and the circumference. Therefore, length BC is also 7.5\text{ cm}
Example 2: Using Multiple Circle Theorems
You may also come across problems where you need to use multiple circle theorems to find the solutions.
Find the size of angle AOC
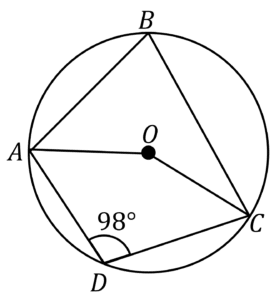
[4 marks]
Immediately, we cannot find the angle at the centre. Let’s consider which rules would allow us to find the angle at the centre…
Rule 6 allows us to find the angle at the centre, but to do this, we will need the angle subtended on the circumference, ABC
So how can we find this angle? The shape within the circle is a cyclic quadrilateral, and the angle we have been given, ADC is opposite the angle we want to find, ABC. And, using rule 7, we know these angles add to 180\degree
Therefore, angle ABC,
180-98=82\degree
Now we can go back to rule 6, and we know the angle at the centre is double the angle at the circumference, so angle AOC,
2\times 82 = 164\degree
Circle Theorems Example Questions
Question 1: Find the size of the angle ACO.
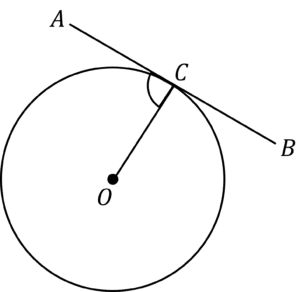
[2 marks]
We can use rule 2 here. A tangent and a radius will always meet at 90\degree. Therefore,
Angle ACO is 90\degree
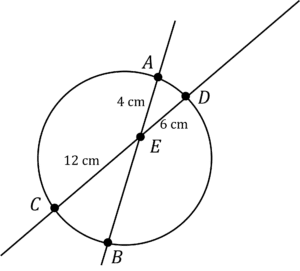
Question 2: In the following diagram,
AE=4\text{ cm}\\
DE=6\text{ cm}\\
CE=12\text{ cm}\\
Find length EB
[2 marks]
Even though the chords are extended here, they still intersect within the circle, and so we use rule 9 part 1, internal intersection,
AE\times EB = CE\times ED
Make sure you check that the A, B, C, D in your diagram match up to those in the rule, or change them accordingly. In this case, the diagram does match up, so:
4\times EB = 12\times6\\
4\times EB=72
EB=18\text{ cm}
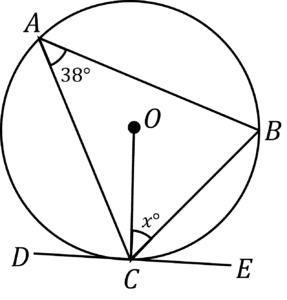
Question 3: Work out the size of angle x in the diagram below.
[4 marks]
You may notice this diagram is a triangle met with a tangent, similarly to the alternate segment theory (rule 8), and so, we’ll start by using this.
This rule tells us that angle BCE is 38\degree
Now, we can employ another rule.
As the tangent is meeting a radius, we know angle OCE is 90\degree (using rule 2). This means we can work out x,
x=90-38=52\degreeQuestion 4: Work out the size of angle x

[4 marks]
Firstly, we can notice that the line going through the chord is a perpendicular bisector to the chord – it has a right angle and splits the chord into two equal lengths. And so, using rule 1, this bisector must pass through the centre.
This means this line is also a diameter.
Thus, we can use rule 4, an angle subtended from the diameter is always 90\degree. Therefore, x=90\degree
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.