Dividing Fractions
Dividing Fractions Revision
Dividing Fractions
Before you look into dividing fractions, make sure you know how to multiply them first – click here multiplying fractions if you’re not sure. The method for dividing fractions follows the keep, change, flip process, or KFC if it helps you remember (though be careful as those letters are technically not in the right order). The process looks like:
1. Keep the first fraction as it is;
2. Change the division sign to a multiplication;
3. Flip the second fraction.
Once you’ve done this, your division becomes a multiplication – i.e. something we know how to do. Let’s see an example of how this works in practice. Covering the basics of fractions will help with this topic.
Example 1: Dividing Fractions
Evaluate \dfrac{4}{11}\div \dfrac{5}{9}.
So, we want to keep the first fraction as it is, change the \div to a \times, and flip the second fraction. Doing this, our calculation becomes
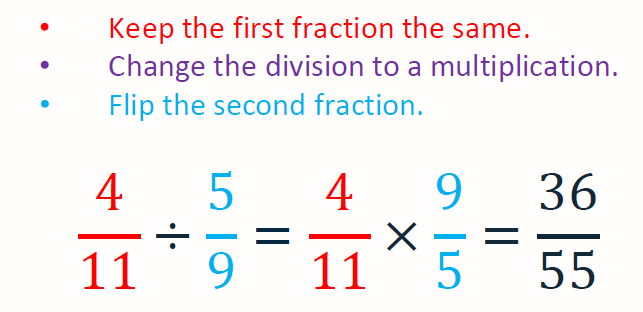
Example 2: Dividing Whole Numbers by Fractions
Evaluate 6\div\dfrac{5}{9}.
To divide a whole number by a fraction (or vice versa), remember that any number divided by 1 is just itself. So, we can write
6=\dfrac{6}{1}
Therefore, we can write
6\div \dfrac{5}{9}=\dfrac{6}{1}\div\dfrac{5}{9}
Now this just looks like a normal fraction division. So, apply the ‘keep, change, flip’ rule and doing the calculation, we get
\begin{aligned}\dfrac{6}{1}\div\dfrac{5}{9} &= \dfrac{6}{1}\times\dfrac{9}{5} \\ &=\dfrac{6\times 9}{1\times 5} \\ &=\dfrac{54}{5}\end{aligned}
Example 3: Dividing Mixed Fractions
Evaluate 4\frac{1}{3}\div\dfrac{5}{6}. Write your answer in its simplest form.
To divide a mixed number by a fraction (or vice versa), first convert the mixed number to an improper fraction.
4\frac{1}{3}=\dfrac{(4\times3)+1}{3}=\dfrac{13}{3}
So, we can now write the calculation to look like a normal division:
4\frac{1}{3}\div\dfrac{5}{6}=\dfrac{13}{3}\div\dfrac{5}{6}
Now we can apply the ‘keep, change, flip’ rule and do the calculation as usual.
\begin{aligned}\dfrac{13}{3}\div\dfrac{5}{6} &= \dfrac{13}{3}\times\dfrac{6}{5} \\ &=\dfrac{13\times 6}{3\times 5} \\ &=\dfrac{78}{15}\end{aligned}
Now, we must simply the fraction. Cancelling a factor of 3 from top and bottom, we get
\dfrac{78}{15}=\dfrac{26}{5}
This cannot be simplified further, so we’re done.
Note: if negative numbers are involved, normal rules of dividing apply:
1. If you divide one positive fraction with one negative fraction (or vice versa), the answer should be negative.
2. If you divide one negative fraction by another negative fraction, the answer should be positive.
Dividing Fractions Example Questions
1) Evaluate \dfrac{2}{15}\div\dfrac{3}{4}
To divide fractions, we need to Keep, Change, and Flip.
Changing the division sign to a multiplication, and flipping the second fraction we get,
\dfrac{2}{15}\div\dfrac{3}{4}=\dfrac{2}{15}\times\dfrac{4}{3}
Thus,
\dfrac{2}{15}\times\dfrac{4}{3}=\dfrac{2\times 4}{15\times 3}=\dfrac{8}{45}
2) Evaluate \dfrac{3}{7} \div 4
Firstly, we can write the whole number 4 as a fraction with a denominator of 1.
4=\dfrac{4}{1}
Then, the calculation becomes,
\dfrac{3}{7}\div\dfrac{4}{1}
Applying ‘keep, change, flip’ we get,
\dfrac{3}{7}\div\dfrac{4}{1}=\dfrac{3}{7}\times\dfrac{1}{4}
Hence,
\dfrac{3}{7}\times\dfrac{1}{4}=\dfrac{3\times 1}{7\times 4}=\dfrac{3}{28}
3) Evaluate \dfrac{2}{3}\div -\dfrac{8}{3}
Give your answer in its simplest form.
We’re dividing a positive fraction by a negative fraction, so the result should be a negative number.
Firstly, apply ‘keep, change, flip’ to get
\dfrac{2}{3}\div -\dfrac{8}{3}=\dfrac{2}{3}\times -\dfrac{3}{8}
Then, doing the multiplication, we get
\dfrac{2}{3}\times -\dfrac{3}{8}=-\dfrac{2\times 3}{3\times 8}=-\dfrac{6}{24}
Finally, cancelling out a factor of 6 from both top and bottom, we get,
-\dfrac{6}{24}=-\dfrac{1}{4}
4) Work out \dfrac{15}{13} \div \dfrac{11}{10}
Give your answer in its simplest form.
To divide fractions, we need to Keep, Change, and Flip.
Changing the division sign to a multiplication, and flipping the second fraction we get,
\dfrac{15}{13} \div \dfrac{11}{10} = \dfrac{15}{13} \times \dfrac{10}{11}
Hence,
\dfrac{15}{13} \times \dfrac{10}{11} = \dfrac{15 \times 10}{13 \times 11} = \dfrac{150}{143}
This can not be simplified so is the final answer.
To divide fractions, we need to Keep, Change, and Flip.
Changing the division sign to a multiplication, and flipping the second fraction we get,
\dfrac{15}{13} \div \dfrac{11}{10} = \dfrac{15}{13} \times \dfrac{10}{11}
Hence,
\dfrac{15}{13} \times \dfrac{10}{11} = \dfrac{15 \times 10}{13 \times 11} = \dfrac{150}{143}
This can not be simplified so is the final answer.
5) Work out 2\dfrac{1}{3} \div \dfrac{1}{3}
Give your answer in its simplest form.
Firstly, we convert the mixed fraction to an improper fraction,
2\dfrac{1}{3} =\dfrac{7}{3}
Changing the division sign to a multiplication, and flipping the second fraction, we find,
\dfrac{7}{3}\div\dfrac{1}{3}=\dfrac{7}{3}\times\dfrac{3}{1}
Thus,
\dfrac{7}{3}\times\dfrac{3}{1}=\dfrac{7\times 3}{3\times 1}=\dfrac{21}{3}=7







