Density Mass Volume
Density Mass Volume Revision
Density Mass Volume
Density is a measure of how tightly the mass of an object is packed into the space it takes up. It can be calculated by dividing mass by volume.
Make sure you are happy with the following topics before continuing.
Density Mass Volume – Formula
Density, mass and volume are all related by the formula,
d = \dfrac{m}{V}
where d is density, V is volume, and m is mass. This can be rearranged in order to find volume or mass depending on which quantities you are given and what the question asks you to find.
Mass is normally measured in grams, g, or kilograms, kg, whereas, volume is normally measured in cubic centimetres, cm^3, or cubic metres, m^3.
This means when dividing mass by volume, the resulting units are typically grams per cubic centimetre (g/cm^3), or kilograms per cubic metre (kg/m^3). These are compound units (for more information, see conversions revision).
Density Mass Volume – Formula Triangle
A handy way of remembering how to calculate either density, mass or volume is to use the triangles below.
The horizontal line means divide and the \times symbol means multiply.
We then cover up the one we want to find (represented by a red circle) and carry out the calculation with the other two values from the triangle.
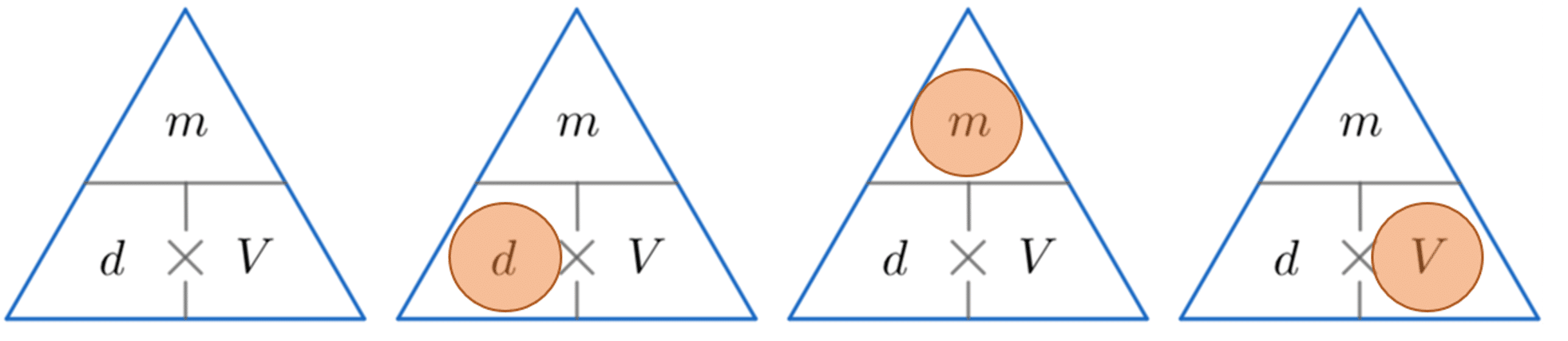
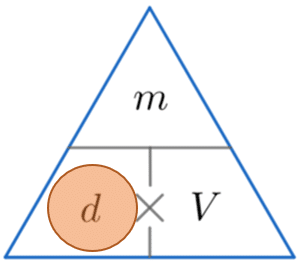
Example 1: Calculating Density
An object has a mass of 570 g and a volume of 2280 cm^3. Calculate its density.
[2 marks]
We’re looking for density, so constructing the triangle and covering d, we see we must divide the mass by the volume. So
\text{density } = \dfrac{570}{2280} = 0.25 g/cm^3

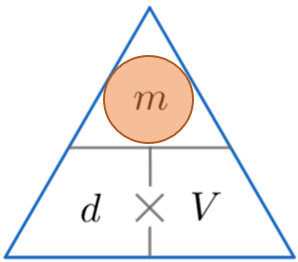
Example 2: Calculating Mass
A cat has volume 0.004 m^3 and density 980 kg/m^3. Calculate the mass of the cat.
[2 marks]
We’re looking for mass, so constructing the triangle and covering m, we see that to calculate the mass we must multiply the density by the volume. So
\text{ Mass } = 980 \times 0.004 = 3.92 kg

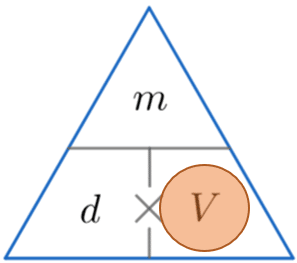
Example 3: Calculating Volume
A bottle of water has a density of 1000 kg/m^3 and mass of 0.5 kg. Calculate the volume of the water bottle giving your answer in litres.
[2 marks]
We’re looking for volume, so covering V, we must divide the mass by the density. So
\text{ Volume } = \dfrac{0.5}{1000} = 0.0005 m^3
Multiplying this by 1000 to convert into litres, gives us the final answer,
\text{ Volume } = 0.5 L

Density Mass Volume Example Questions
Question 1: A bottle is filled with 2 kg of olive oil which has a density of 0.925 g/cm^3. What is the volume of the olive oil to the nearest cm^3?
[2 marks]
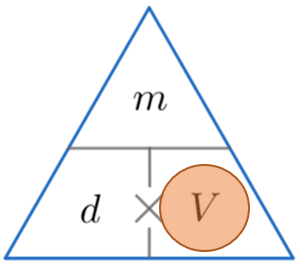
We are calculating the volume, so by covering up the V we can see from the triangle above that we have to divide m by d.
Before we can do this, however, we have to make sure that we have the correct units. The mass is in kilograms, but the density is in grams per cubic centimetre. This means that we have to first convert the kilograms into grams before proceeding.
2 kg = 2000 g
Therefore, the volume of the olive oil can be calculated as follows:
\text{Volume} = 2000 \div 0.925 = 2162cm^3
Question 2: A cube with side length 7 m has a density of 10,800,000 kg/m^3. Work out the mass of the cube.
[2 marks]
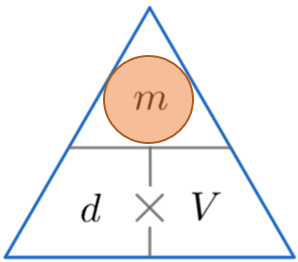
We are calculating the mass, so by covering up the m we can see from the triangle above that we have to multiply d by V.
However, we don’t know the volume, but we do know that the shape is a cube with a side length of 7 m, so the volume of the cube is:
7 \times 7 \times 7 = 343 m^3
Now that we know the volume, we can multiply it by the density in order to calculate the mass:
\text{Mass } = 343 \times 10,800,000 = 3,704,400,000 kg
Question 3: A concrete block weighing 2460 kg has a volume of 1.2 m^3. What is the density of the block?
[2 marks]
To calculate the answer here, we need to recall the formula:
\text{ density} = \text{ mass} \div \text{ volume}
In this question, the mass is 2460kg and the volume is 1.2 m^3, so we simply need to substitute these values into the formula as follows:
\text{ Density} = 2460 kg \div \, 1.2 m^3 = 2050 kg/m^3
Question 4: Metal A has a density of 5 g/cm^3 and metal B has a density of 3 g/cm^3.
1200 g of metal A and 600 g of metal B are melted and mixed and then recast into a block.
a) What is the volume of the block?
b) What is the density of the block?
[4 marks]
a) In order to calculate the overall volume of the block, we need to add the volume of metal A and the volume of metal B. Although we don’t have the volume of either metal, we have been given their masses and densities, so we can calculate the volume of each metal accordingly.
By rearranging the density formula, or using the triangle, we can work out how to calculate the volume:
\text{density} = \text{ mass}\div \text{ volume}
So:
\text{volume} = \text{ mass}\div \text{ density}
The volume of metal A can be calculated as follows:
1200 g \div \, 5 g/cm^3 = 240 cm^3
The volume of metal B can be calculated as follows:
600 g \div \, 3 g/cm^3 = 200 cm^3
Therefore, if metal A has a volume of 240 cm^3 and B has a volume of 200 cm^3, then their combined volume is simply:
240 cm^3 + 200 cm^3 = 440 cm^3
b) As we know from question a), the newly-formed block has a volume of 440 cm^3.
We know that the mass of metal A was 1200 g and the mass of metal B was 600 g, so mass of the block is:
1200 g + \, 600 g = 1800 g
The density of this block can be calculated by dividing the mass by the volume as follows:
1800 g \div \, 440 cm^3 = 4.09 g/cm^3
Question 5: Metal A has a density of 3.2 g/cm^3 and metal B has a density of 5.5 g/cm^3. Metal C is made from combining metal A and metal B in a ratio of 3:7. To one decimal place, what is the density of metal C if it has a mass of 2500 g?
[4 marks]
This is quite a challenging question with a lot of calculations going on.
Since we have been given the mass of metal C and the ratio of metal A and metal B in metal C, we can therefore calculate the mass of metal A and metal B. If the ratio of metal A to metal B is 3 : 7, that means that \frac{3}{10} of the mass of metal C comes from metal A and the remaining \frac{7}{10} is metal B. (We are dealing in tenths here since the sum of the ratio is 10.)
The mass of metal A can be calculated as follows:
2500 g \times \dfrac{3}{10} = 750 g
The mass of metal B can be calculated as follows:
2500 g \times \dfrac{7}{10} = 1750 g
We now know both the mass and density of both metals A and B, meaning we can work out their respective volumes.
Since
\text{density} = \text{ mass} \div \text {volume}
then
\text{volume} = \text{ mass} \div \text {density}
The volume of metal A can be calculated as follows:
750 g \div \, 3.2 g/cm^3 = 234.375 cm^3
The volume of metal A can be calculated as follows:
1750 g \div \, 5.5 g/cm^3 = 318.18 cm^3
If metal A has a volume of 234.375 cm^3 and metal B has a volume of 318.18 cm^3, then their combined volume is the volume of metal C.
Volume of metal C = 234.375 + 318.18 = 552.5568 cm^3
We now know both the mass and volume of metal C, so we are now able to calculate its density.
Density of metal C = 2500 g \div \, 552.5568 cm^3 = 4.5 g/cm^3





