Conversion Graphs

GCSEKS3Level 4-5AQACambridge iGCSEEdexcelEdexcel iGCSEOCRWJEC

Conversion Graphs Revision

Conversion Graphs

A conversion graph is a tool that we use to convert between different units. All graphs you come across will be straight-line graphs with one unit on the $x$ -axis and the other on the $y$ -axis. You have to know how to construct and use a conversion graph given a conversion rate.

Make sure you are happy with the following topics before continuing.

Conversions revision

Conversion Graphs Method

When using conversion graphs, we may be asked to find both ways of converting between two units. To find these conversions it helps to draw on the graph.

Example: Shown is a conversion graph for converting between litres and fluid ounces.

a) Convert $\textcolor{Red}{2.5}$ litres into fluid ounces;

Step 1: Starting from $\textcolor{Red}{2.5}$ on the $y$ -axis, draw a horizontal line until you meet the line.

Step 2: From this point, draw a vertical line down until it meets the $x$ -axis (green line).

Step 3: Read the value where your line met the $x$ -axis and you have the result of the conversion.

We can see that the $\textcolor{Red}{2.5}$ litre line ends up at $\textcolor{darkorange}{88}$ fluid ounces on the $x$ -axis, so $\textcolor{red}{2.5}$ litres $\approx \textcolor{darkorange}{88}$ fluid ounces.

b) Convert $\textcolor{darkorange}{24}$ fluid ounces into litres.

We now have to convert in the other direction, so we simply reverse the process: draw up to the graph first (the red line), then across, and this time read the result off the $y$ -axis.

We see that the $\textcolor{darkorange}{24}$ fluid ounce line ends up between $0.6$ and $0.8$ on the $y$ -axis. So $\textcolor{darkorange}{24}$ fluid ounces $\approx \textcolor{red}{0.7}$ litres.

Example: Conversion Graphs

Shown is a conversion graph for converting between miles driven and the price of a hire car.

[2 marks]

a) Convert $£100$ into Miles:

Drawing a line (the green line) across from $100$ on the $y$ -axis to the conversion graph (the blue line) and then down to the $x$ -axis, gives a conversion of

$£100 = 125$ miles

b) $300$ Miles to $£$ ‘s:

Drawing a line (the red line) up from $300$ on the $x$ -axis to the conversion graph and then across to the $y$ -axis, gives a conversion of

$300$ miles $= £170$

Conversion Graphs Example Questions

Question 1: Below is a graph that can be used to convert between pints and litres. Using the graph, find an approximate value for the following conversions:

a) $3$ litres to pints

b) $3.8$ pints to litres

[4 marks]

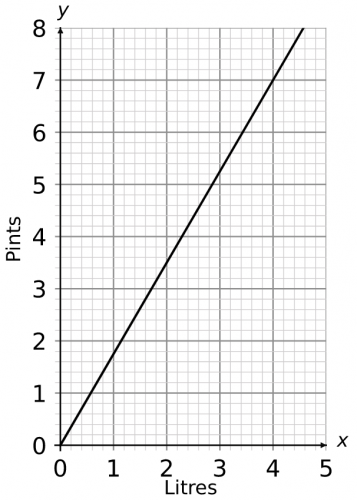
a) since we are converting litres to pints, we need to locate the value $3$ on the horizontal ( $x$ ) axis and draw a line vertically upwards until it touches the black solid line of the graph. Then we need to draw a line from this point horizontally to the left to find the corresponding value on the vertical ( $y$ ) axis. This value falls between $5.2$ and $5.4$ pints, so the approximate answer is

$3$ litres $= 5.3$ pints

b) since we are converting pints to litres, we need to locate $3.8$ on the vertical ( $y$ ) axis and draw a line horizontally to the right until it touches the blue line of the graph. Then we need to draw a line from this point vertically down to find the corresponding value on the horizontal ( $x$ ) axis. This value falls between $2$ and $2.2$ litres. Since it is closer to $2.2$ than $2$ , the approximate answer is

$3.8$ pints $=2.15$ litres

Save your answers with

Gold Standard Education

Question 2:

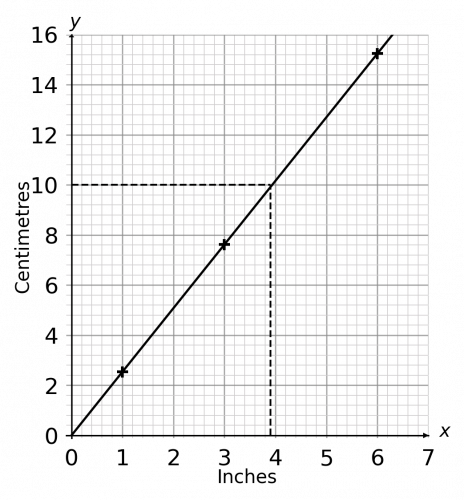
a) Using the conversion rate shown below, draw a conversion graph to convert inches and centimetres. The graph must be drawn in the range of $0$ to $6$ inches. (To make it easier to compare your answer to the solution, display inches on the $x$ -axis and cm on the $y$ -axis.)

$1 \text{ inch }\equiv 2.54 \text{ cm}$

b) Using your graph, convert $10$ cm to inches.

[4 marks]

a) We know that $1$ inch equals $2.54$ cm, so we can plot the point $(1, 2.54)$ on the graph.

If $1$ inch equals $2.54$ cm, then the cm equivalent of $3$ inches can be calculated as follows:

$3 \text{ inches} = 3 \times 2.54 \text{ cm} = 7.62 \text{ cm}$

As a result, we can now plot the point $(3, 7.62)$ on the graph.

If $1$ inch equals $2.54$ cm, then the cm equivalent of $6$ inches can be calculated as follows:

$6\text{ inches} = 6 \times 2.54 \text{ cm} = 15.24 \text{ cm}$

As a result, we can now plot the point $(6, 15.24)$ on the graph.

Now all we need to do is join the points, as per the graph below.

(We could have skipped one of the steps above as you only need to work out two points in order to draw a straight line, although $3$ points does ensure that you haven’t made an error. If you have plotted $3$ points and they are not in line, then one of your points has been calculated incorrectly.)

b) To use this graph to convert $10$ cm to inches, we must locate $10$ cm on the vertical ( $y$ ) axis and draw a horizontal line to the right until it touches the line of the graph. We then draw line vertically down to find the corresponding value on the horizontal ( $x$ ) axis. The value on the $x$ -axis is halfway between $3.8$ and $4$ , so

$10$ cm $\approx 3.9$ inches

Save your answers with

Gold Standard Education

Question 3: Using the conversion graph find approximate values for:

a) the number of litres in $4$ pints

b) the number of pints in $5$ litres

[4 marks]

a) For this first conversion, we are converting litres to pints. Since pints is on the horizontal $x$ axis, locate $4$ on this axis and go up until you touch the line. Then go across to the corresponding value on the vertical $y$ axis. We can see that this line touches between $2.2$ litres and $2.4$ litres, so we can say that

$4$ pints $\approx 2.3$ litres

b) For the second conversion, we are converting pints to litres. Since litres is on the vertical $y$ axis, locate $5$ on this axis and go across to the right until you touch the line. Then go down to the corresponding value on the horizontal $x$ axis. We can see that this line touches between $8.6$ pints and $8.8$ pints so we can say that

$5$ litres $\approx 8.7$ pints