Trigonometric Equations

GCSELevel 8-9Cambridge iGCSE

Trigonometric Equations Revision

Solving Trigonometric Equations

Using what we know already about sine, cosine, and tangent, (or sin, cos, and tan), we need to be able to solve equations involving these.

For example,

$\sin(x)=\dfrac{\sqrt{3}}{2}$

We will look at how to solve equations like this graphically, and algebraically.

Solving Graphically

We can look at the sin, cos, and tan graphs to solve equations.

For example, estimate the solutions to

$\sin(x)=0.2$

$\cos(x)=0.2$

$\tan(x)=0.2$

Between $0\degree$ and $360\degree$

Sine graph

To solve, draw a line on the sine graph at $y=0.2$ and read off the solutions:

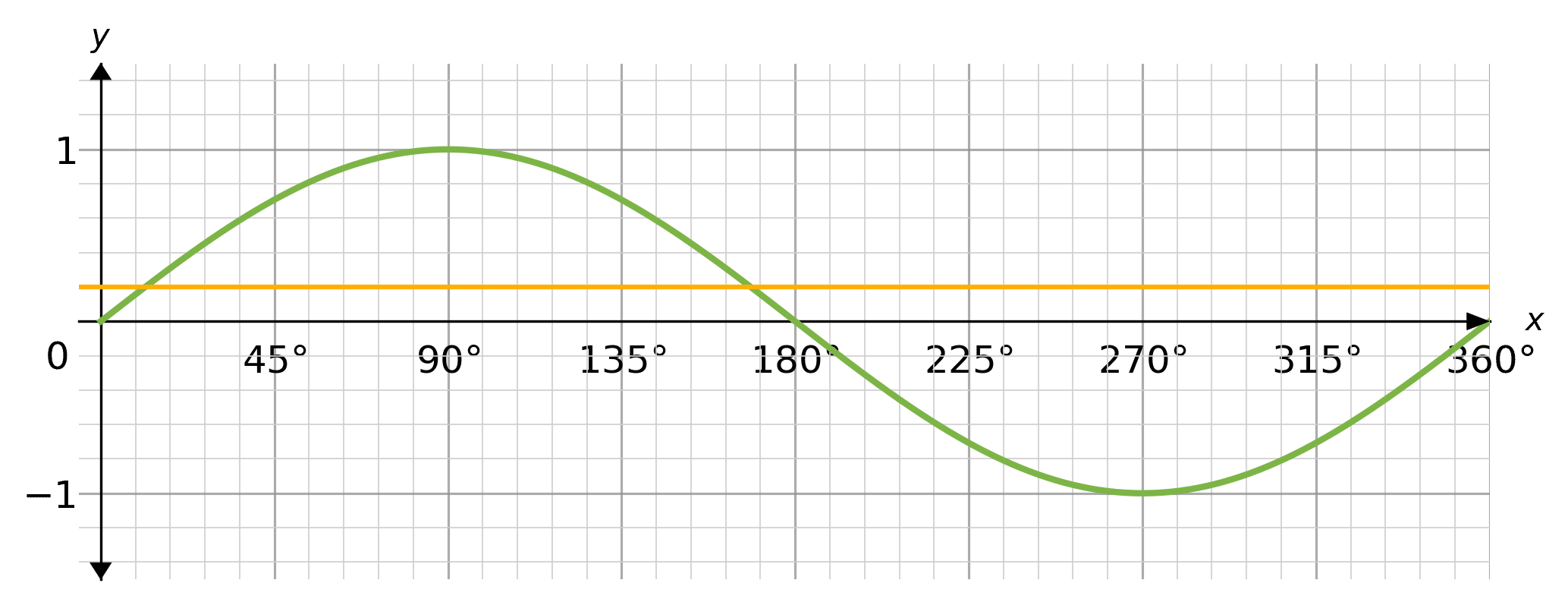
The yellow line crosses the sin graph at approximately $x=11\degree$ and $x=169\degree$ . These are the approximate solutions to the equation $\sin(x)=0.2$

Cosine graph

To solve, draw a line on the cosine graph at $y=0.2$ and read off the solutions:

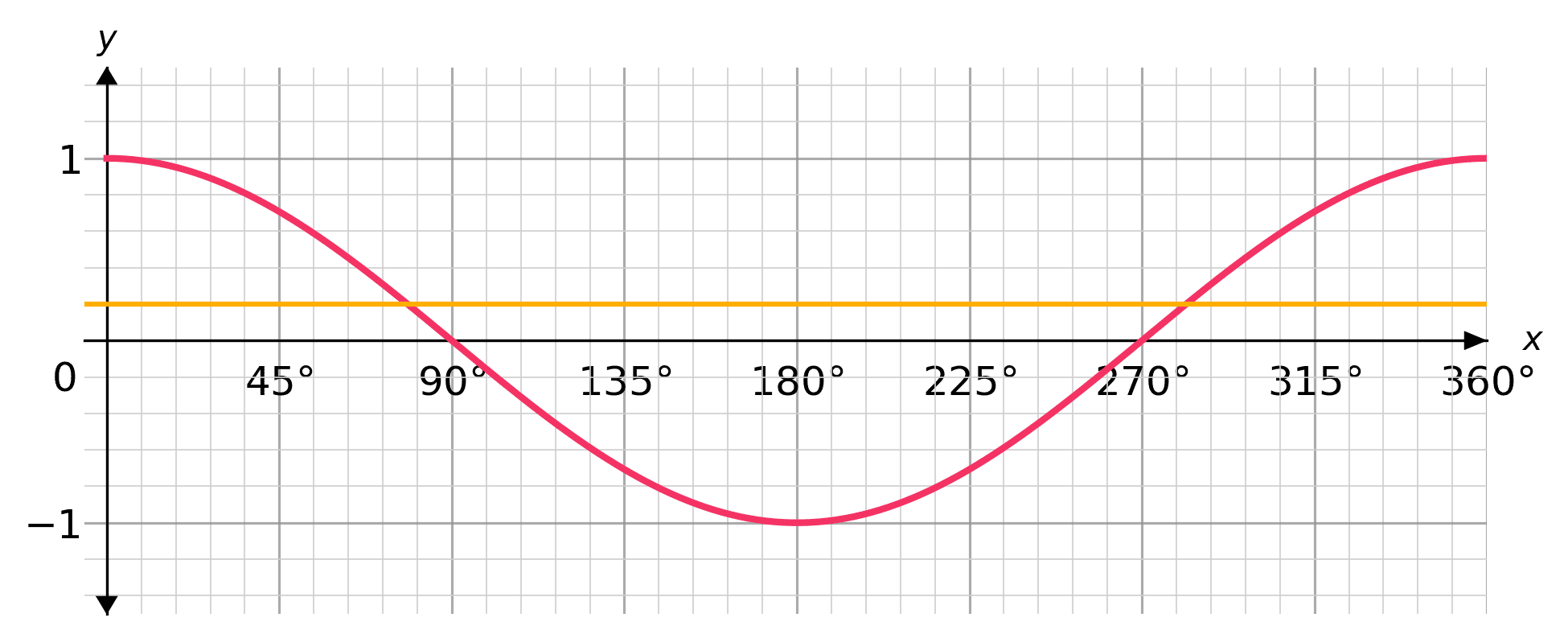
The yellow line crosses the cos graph at approximately $x=78\degree$ and $x=282\degree$ . These are the approximate solutions to the equation $\cos(x)=0.2$

Tangent graph

To solve, draw a line on the tangent graph at $y=0.2$ and read off the solutions:

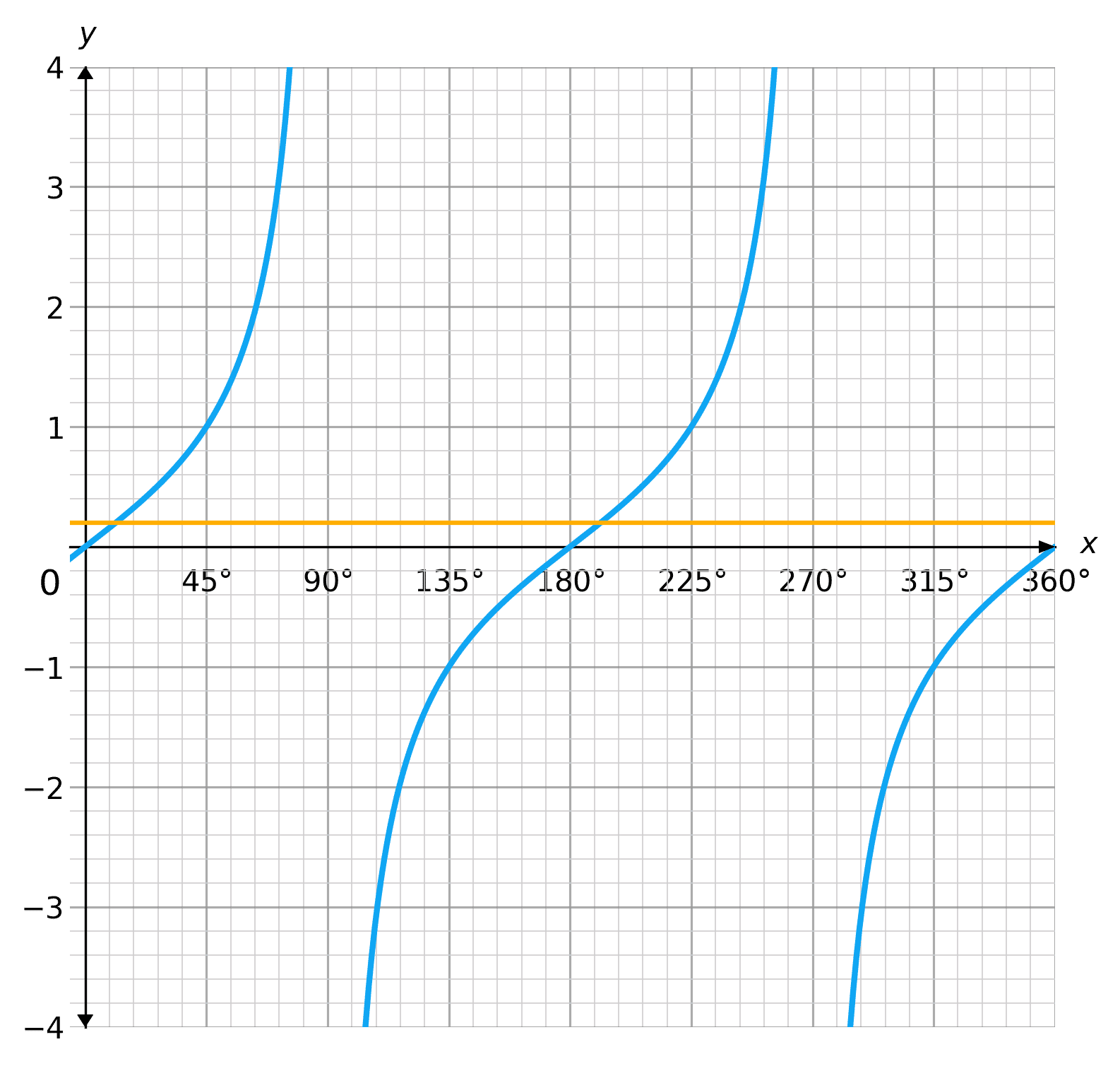
The yellow line crosses the tan graph at approximately $x=11\degree$ and $x=191\degree$ . These are the approximate solutions to the equation $\tan(x)=0.2$

Solving Algebraically – Sine

Sometimes, you may not be given a graph, and so, it would not be possible to accurately solve a trigonometric equation graphically. In this case, we would solve the equation algebraically, using our calculator.

You will always be asked to solve algebraic trigonometric equations for values between $0\degree$ and $360\degree$ .

We can use our calculator, and the properties of sine to solve trigonometric equations involving sine.

For example:

$\sin(x)=\dfrac{\sqrt{3}}{2}$

We can use our calculator:

$\sin^{-1}\left(\dfrac{\sqrt{3}}{2}\right)=60\degree$

However, our calculator only gives us one value, but we know there are more solutions between $0\degree$ and $360\degree$ .

As the sine graph is positive between $0\degree$ and $180\degree$ , we can find the other value by…

$180\degree-60\degree=120\degree$

So the final solutions are $x=60\degree, 120\degree$ .

Solving Algebraically – Cosine

We can use our calculator, and the properties of cosine to solve trigonometric equations involving cos.

For example:

$\cos(x)=\dfrac{1}{2}$

We can use our calculator:

$\cos^{-1}\left(\dfrac{1}{2}\right)=60\degree$

However, our calculator only gives us one value, but we know there are more solutions between $0\degree$ and $360\degree$ .

As the cosine graph is positive between $0\degree$ and $360\degree$ , we can find the other value by…

$360\degree-60\degree=300\degree$

So the final solutions are $x=60\degree, 300\degree$ .

Solving Algebraically – Tangent

We can use our calculator, and the properties of tangent to solve trigonometric equations involving tan.

For example:

$\tan(x)=\sqrt{3}$

We can use our calculator:

$\tan^{-1}(x)=60\degree$

However, our calculator only gives us one value, but we know there are more solutions between $0\degree$ and $360\degree$ .

As the tangent graph repeats every $180\degree$ , we can find the other value by…

$60\degree+180\degree=240\degree$

So the final solutions are $x=60\degree, 240\degree$ .

Example 1: Solving Graphically

Use the cosine graph to estimate the solutions to

$\cos(x)=0.4$

between $0\degree$ and $360\degree$

[3 marks]

Draw the line $y=0.4$ onto the graph and read off the solutions:

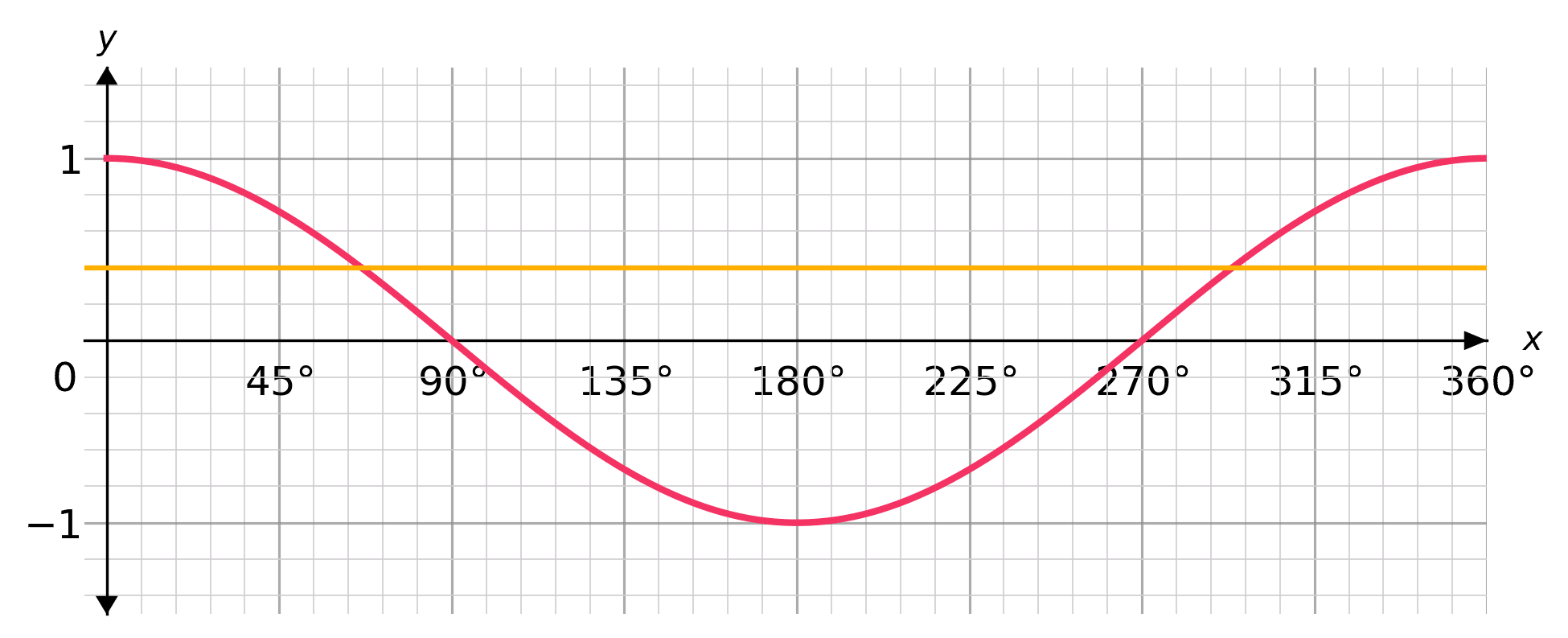
The solutions are approximately $x=68\degree$ and $x=293\degree$

Example 2: Solving Algebraically

Solve

$\sin(x)=\dfrac{5}{8}$

For values between $0\degree$ and $360\degree$ , giving your answers to $2$ decimal places.

[3 marks]

Let’s find the first value using our calculator

$\sin^{-1}\left(\dfrac{5}{8}\right)=38.68\degree$

As sin is positive between $0\degree$ and $180\degree$

$180-38.68=141.32\degree$

Solutions: $x=38.68\degree, 141.32\degree$

Trigonometric Equations Example Questions

Question 1: Graphically solve the equation

$\tan(x)=1.3$

approximately, between $0\degree$ and $360\degree$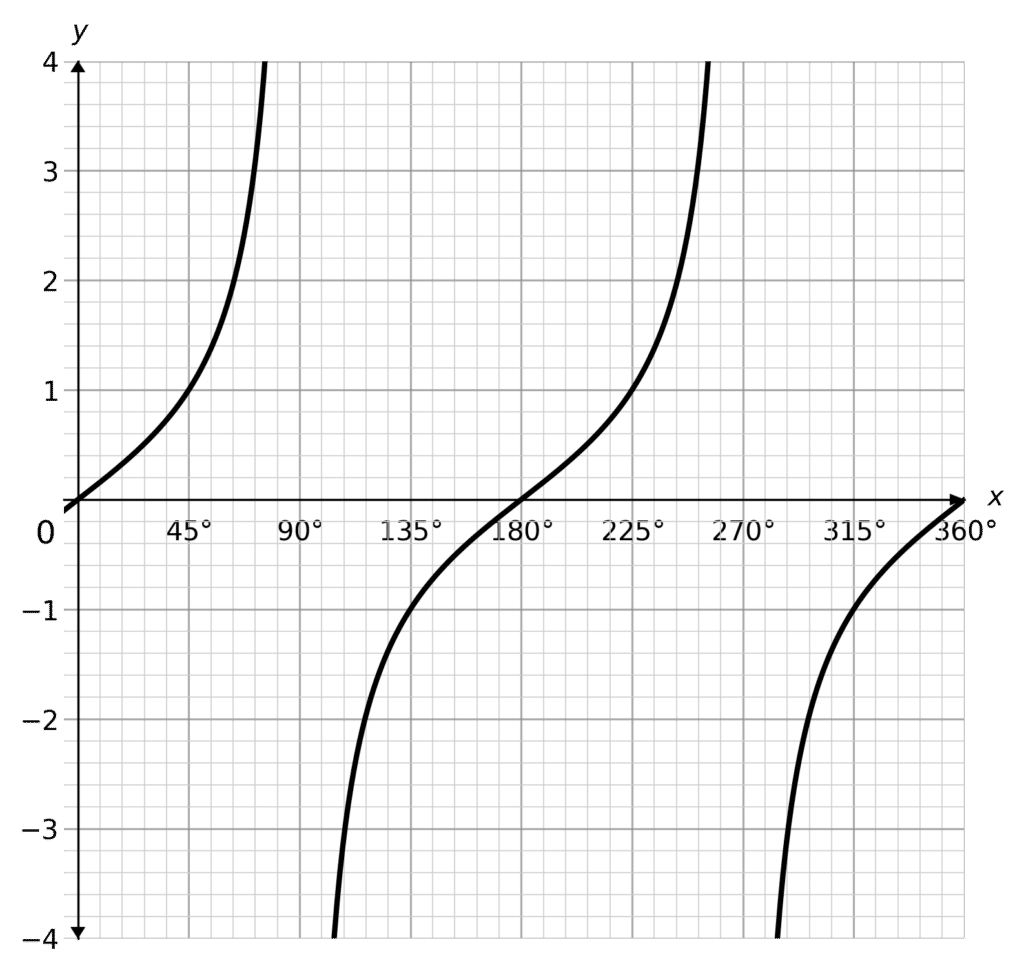

[3 marks]

Draw the line $y=1.3$ and read the solutions:

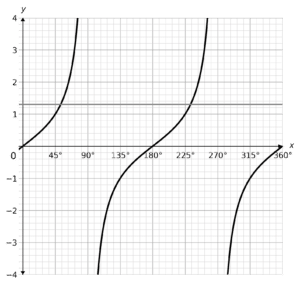
Solutions are approximately $x=55\degree\text{, }235\degree$

Save your answers with

Gold Standard Education

Question 2: Solve $\tan(x)=\dfrac{4}{7}$ between $0\degree$ and $360\degree$ , giving your answer(s) to the nearest whole number.

[3 marks]

Using a calculator:

\tan^{-1}\left(\dfrac{4}{7}\right)=30\degree

Find the other value:

30+180=210\degree

Save your answers with

Gold Standard Education

Question 3: Given that $\cos^{-1}(x)=45\degree$ , find another solution to $\cos^{-1}(x)$ between $0\degree$ and $360\degree$ , and work out the value of $x$ .

[4 marks]

As we are solving for cos, the other value will be