Solving Quadratic Equations by Factorisation
Solving Quadratic Equations by Factorisation Revision
Solving Quadratic Equations by Factorisation
Quadratic equations are equations that take the form, or can be rearranged to the form,
ax^{2}+bx+c=0
These can be solved by factorising the ax^{2}+bx+c part of the equation into two brackets, then setting each bracket to 0 to derive two solutions, called roots.
Note: Not all quadratics can be factorised, so not all quadratics can be solved with this method.
Make sure you are happy with the following topics before continuing:
How to Solve a Quadratic Equation by Factorisation
The general steps to solve a quadratic by factorisation are as follows:
Step 1: If necessary, rearrange the quadratic into the form ax^{2}+bx+c=0
Step 2: Factorise the quadratic into two brackets (px+q)(rx+s)=0
Step 3: Get two solutions by solving the two linear equations px+q=0 and rx+s=0
Example: Solve by factorisation x^{2}+4x+3=0
Step 1: This quadratic is already in the form we want, so we don’t need to rearrange.
Step 2: Factorise the quadratic: x^{2}+4x+3=(x+3)(x+1)=0
Step 3: Set both brackets to 0 and solve:
x+3=0\rightarrow x=-3 and x+1=0\rightarrow x=-1
So our two solutions are x=-3 and x=-1
Tip: For quadratics with a=1, we can read the solutions off from the factorisation, as the roots of (x+p)(x+q)=0 are -p and -q. For quadratics with a\neq1 it is more complicated.
Example: Solve by factorisation 2x^{2}-11x=-5
Step 1: Rearrange by adding 5 to both sides: 2x^{2}-11x+5=0
Step 2: Factorise the quadratic: (2x-1)(x-5)=0
Step 3: Set both brackets to 0 and solve:
2x-1=0\rightarrow x=\dfrac{1}{2} and x-5=0\rightarrow x=5
So our two solutions are x=\dfrac{1}{2} and x=5
Note: The reason this method to solve quadratics works is that, once factorised, the quadratic is two brackets that multiply together to give 0. This can only happen when one of the brackets is 0, so we can get solutions by assuming that is the case.
Factorisation and Quadratic Graphs
We can use factorisation to help us sketch a quadratic graph. This is because the roots of the quadratic equation is where the graph crosses the x-axis, so we can factorise to find the roots and use these to help determine the correct shape of the graph.
Example: Sketch the graph y=x^{2}-2x-3
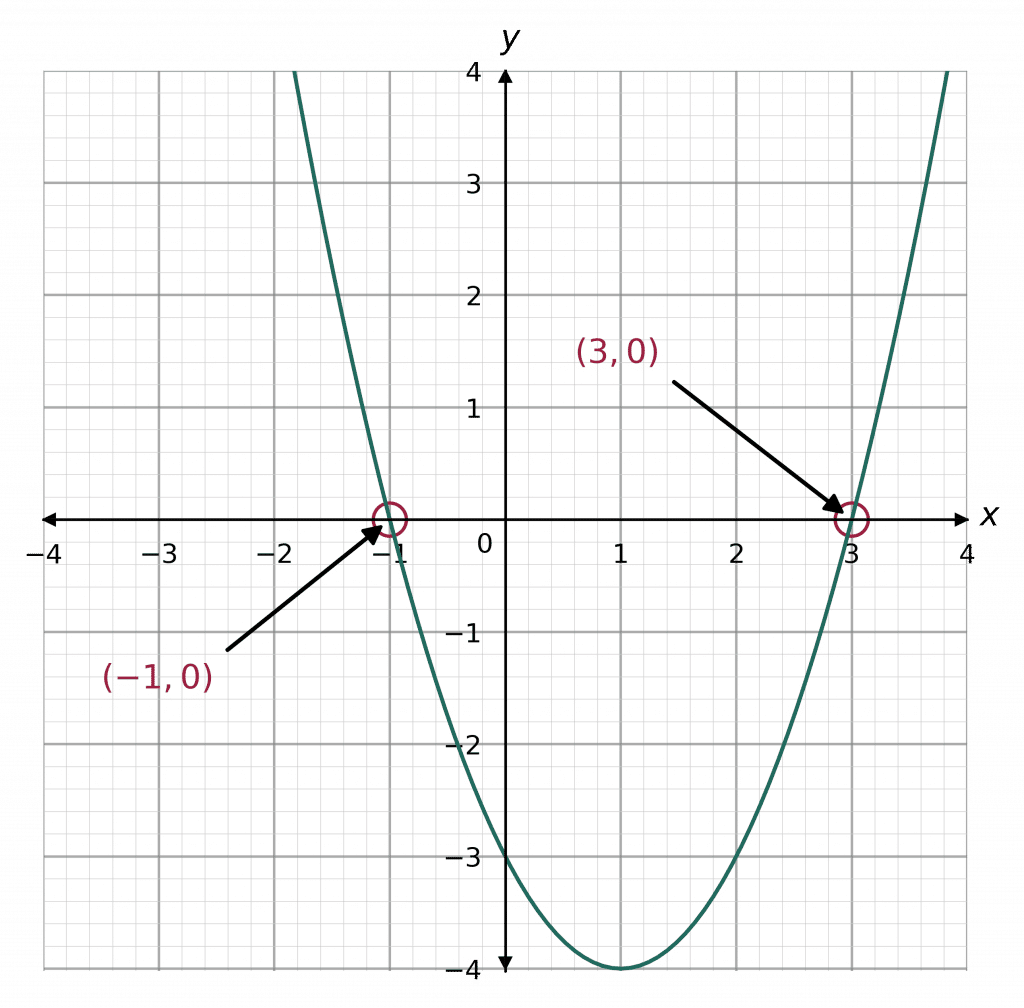
Step 1: For a graph we want it to be in the form y=ax^{2}+bx+c, which we already have. We then set y=0.
x^{2}-2x-3=0Step 2: Factorise the quadratic: (x-3)(x+1)=0
Step 3: Set both brackets to 0 and solve:
x-3=0\rightarrow x=3 and x+1=0\rightarrow x=-1
Alternatively we can use the tip from earlier to read off the roots from the brackets as x=3 and x=-1
Step 4: These roots are the x-intercepts of the graph – the places where the graph crosses the x-axis. So we know the graph crosses the points (3,0) and (-1,0).
Step 5: Find the y-intercept. For a graph of the form y=ax^{2}+bx+c, this is just the number on the end, c. In this example, it is -3, so the graph also goes through (0,-3).
Step 6: Use the points we have found to sketch the graph. The graph on the right was drawn by a computer, a sketch will not need to look as accurate as this. Instead, a sketch only has to be the right shape and cross the axes at the points we found.
Example 1: Solving a Quadratic Equation by Factorisation (a=1)
Solve by factorisation x^{2}=7x-12
[2 marks]
Step 1: Rearrange by subtracting 7x-12 from both sides:
x^{2}-7x+12=0
Step 2: Factorise the quadratic:
x^{2}-7x+12=(x-4)(x-3)=0
Step 3: Find the solutions by setting both brackets equal to 0:
x-4=0\rightarrow x=4 and x-3=0\rightarrow x=3
Alternatively, since a=1, the solutions x=4 and x=3 can be read off from the factorisation.
Example 2: Solving a Quadratic Equation by Factorisation (a\neq1)
Solve by factorisation 5x^{2}+54x-11=0
[3 marks]
Step 1: Rearrange – in this case it is not necessary to do so as the equation is already in the form we want.
Step 2: Factorise the quadratic:
5x^{2}+54x-11=(5x-1)(x+11)=0
Step 3: Set both brackets to 0 and solve:
5x-1=0\rightarrow x=\dfrac{1}{5} and x+11=0\rightarrow x=-11
So the solutions are:
x=\dfrac{1}{5} and x=-11
Example 3: Factorisation and Quadratic Graphs
Sketch the graph y=x^{2}-x-6
[4 marks]
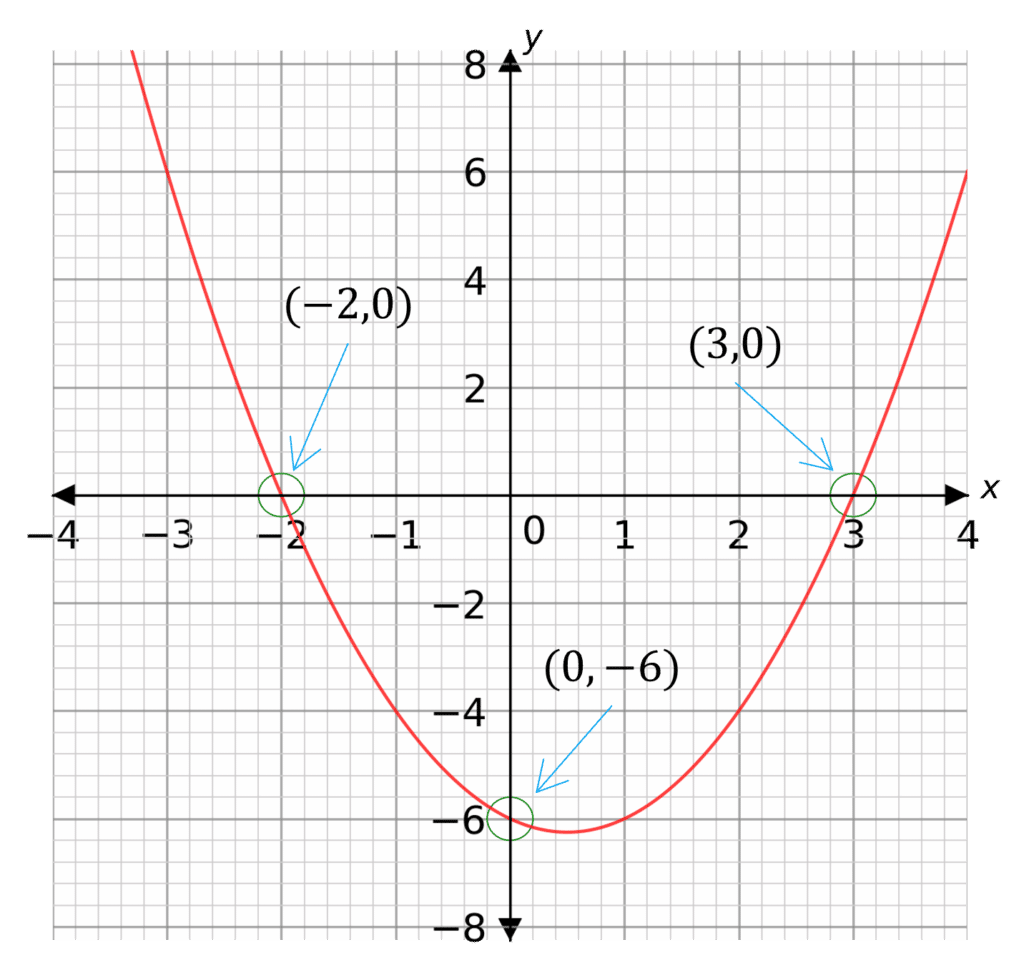
Step 1: This quadratic graph is already in the form we are looking for. The quadratic we want to solve is x^{2}-x-6=0
Step 2: Factorise the quadratic:
x^{2}-x-6=(x-3)(x+2)=0
Step 3: Solve the equation by setting both brackets to 0:
x-3=0\rightarrow x=3 and x+2=0\rightarrow x=-2
Alternatively, the solutions x=3 and x=-2 can be read off from the factorisation.
Step 4: These roots are the x-intercepts of the graph, so we know the graph passes through the points (3,0) and (-2,0)
Step 5: The y-intercept is the number on the end of the quadratic, in this case it is -6, so the graph passes through (0,-6)
Step 6: Sketch the graph, making sure it is the right shape and it crosses the axes at the right points.
Solving Quadratic Equations by Factorisation Example Questions
Question 1: Solve, by factorisation, x^{2}-5x+4=0
[2 marks]
Step 1: Rearrange if necessary – this equation is already in the correct form.
Step 2: Factorise the quadratic:
x^{2}-5x+4=(x-4)(x-1)=0Step 3: Set both brackets to 0 and solve:
x-4=0\rightarrow x=4 and x-1=0\rightarrow x=1
Alternatively, we can read the solutions x=4 and x=1 off from the factorisation.
Question 2: Solve by factorisation: x^{2}=21x+72
[3 marks]
Step 1: Rearrange the equation. In this case we need to subtract 21x+72 from both sides:
x^{2}-21x-72=0Step 2: Factorise the quadratic:
x^{2}-21x-72=(x-24)(x+3)=0Step 3: Set both brackets to 0 and solve:
x-24=0\rightarrow x=24 and x+3=0\rightarrow x=-3
Alternatively, we can read the solutions x=24 and x=-3 off from the factorisation.
Question 3: Solve by factorisation 2x^{2}+11x+12=0
[3 marks]
Step 1: Rearrange if necessary – this equation is already in the correct form.
Step 2: Factorise the quadratic:
2x^{2}+11x+12=(2x+3)(x+4)=0Step 3: Set both brackets to 0 and solve:
2x+3=0\rightarrow x=-\dfrac{3}{2} and x+4=0\rightarrow x=-4
So the solutions are:
x=-\dfrac{3}{2} and x=-4
Question 4: Solve, by factorisation:
x^{2}=7+\dfrac{2x}{3}[4 marks]
Step 1: Rearrange the equation. First multiply by 3:
3x^{2}=21+2xNow subtract 21+2x from both sides:
3x^{2}-2x+21=0Step 2: Factorise the quadratic:
3x^{2}-2x-21=(3x+7)(x-3)=0Step 3: Set both brackets to 0 and solve:
3x+7=0\rightarrow x=-\dfrac{7}{3} and x-3=0\rightarrow x=3
So the solutions are:
x=-\dfrac{7}{3} and x=3
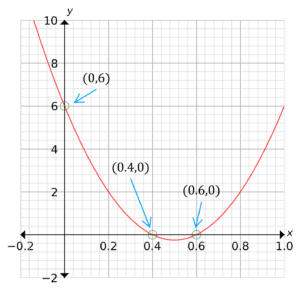
Question 5: Sketch the graph y=25x^{2}-25x+6
[5 marks]
Step 1: This quadratic graph is already in the form we are looking for. The quadratic we want to solve is 25x^{2}-25x+6=0
Step 2: Factorise the quadratic:
25x^{2}-25x-6=(5x-2)(5x-3)=0Step 3: Solve the equation by setting both brackets to 0:
5x-2=0\rightarrow x=0.4 and 5x-3=0\rightarrow x=0.6
Step 4: These roots are the x-intercepts of the graph, so we know the graph passes through the points (0.4,0) and (0.6,0)
Step 5: The y-intercept is the number on the end of the quadratic, in this case it is 6, so the graph passes through (0,6)
Step 6: Sketch the graph, making sure it is the right shape and it crosses the axes at the right points.