Set Notation
Set Notation Revision
Set Notation
Understanding set notation is important when it comes to working with probability. Sets are usually denoted by a singular capital letter, and are either written down as a list of all numbers within that set or by giving a rule.
Definition of Sets
A set can be described by listing all the elements within it e.g. \{1, 3, 5, 7, 9\}. However, for sets with a large amount of elements this is often impractical, so these sets would often be defined by giving a specific rule e.g. \{\text{multiples of }3\}.
The standard notation to show that you are defining a set is to use curly brackets \{\}.
Capital letters are often used to denote the whole set, e.g. K=\{\text{all positive multiples of }2\}. Then a lower case letter would be used to denote an element within this set, e.g. x is an element of K.
Therefore, in this case this set could be described as K=\{x:x \text{ is a positive multiple of } 2\}.
The universal set, denoted by the Greek letter ‘xi‘ or \xi, which is the set that includes all the elements that the elements of another set can be selected from.
Example:
\xi=\{1,2,3,4,5,6,7,8,9,10\}
P=\{\text{prime numbers}\}
Then the elements of P are all the numbers within \xi that are prime, which are 2, 3, 5 and 7.
The Union and Intersection of Sets
The union of two sets can be defined as a set containing all the elements in both sets. This is denoted by a ‘u‘ shaped symbol, \cup, so you would write the union of set A and set B as A\cup B.
The intersection of two sets only includes the elements that are in both sets. This is denoted by a ‘n‘ shaped symbol, \cap, so you would write the intersection of set A and set B as A\cap B.
Example:
X=\{5, 10, 15, 20, 25\}
Y=\{2, 4, 6, 8, 10, 12, 14, 16, 18, 20\}
X\cup Y=\{2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20, 25\}
X\cap Y=\{10, 20\}
10 and 20 appear in both sets, so these are the only elements in the intersection of the two sets.
For the union, elements that appear in both sets should only be listed once.
Defining Sets Using Algebra and Inequalities
Sets will often be defined using algebra and/or inequalities, so you will need to decipher what the description of the set is before being able to work with it.
For example, a set A may be written as \{a:a>2\}, which means that the set A is the set of numbers, a, such that a is greater than 2.
Another example of a description of a set is \{(x,y):y=3x-1\}, which is the set of all the points (x,y) such that y=3x-1.
Example:
\xi=\{\text{positive integers}\}
N=\{x:x<5\}
List all the elements of the set N.
The elements of N must also be contained within the universal set, so the numbers which satisfy both definitions are:
1,2,3 and 4
More Set Notation
To express whether something is an element of a set or not, the symbols \in or \notin are used.
\in = something is an element of a set – e.g. 3 \in \{\text{odd numbers}\}
\notin = something isn’t an element of a set – e.g. 6 \notin \{\text{multiples of }5\}
If a set doesn’t have any elements contained within it, then it is called the empty set, denoted as \{\} or \varnothing.
For example, if set Z=\{\text{prime numbers that are multiples of }4\}, then set Z=\varnothing.
To express how many elements there are within a set, the notation n(A) is used, e.g. n(A)=8 shows that there are 8 elements within the set A.
Using Venn Diagrams to Represent Sets
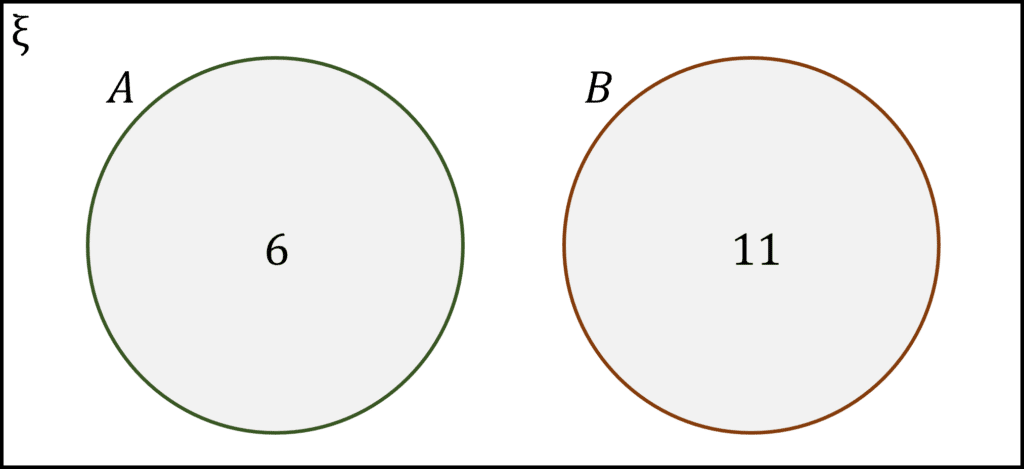
Venn diagrams can be really helpful to visualise sets, especially the union and intersection of them.
Each set is represented by a circle, with all circles contained within a larger rectangle, which represents the universal set \xi.
The circles in a Venn diagram are labelled by a letter, which also corresponds to the set. For sets representing the quantity of something, e.g. the number of girls in a class, a number will be inside the circle.
Intersection and Union
The intersection of sets is represented as where the circles overlap, if the two sets don’t have any shared elements then the circles will not overlap.
The union of sets is represented by the entire space of the circles.
Example:
\xi=\{\text{Positive integers less than }20\}
C=\{\text{Multiples of }3\}
D=\{\text{Multiples of }2\}
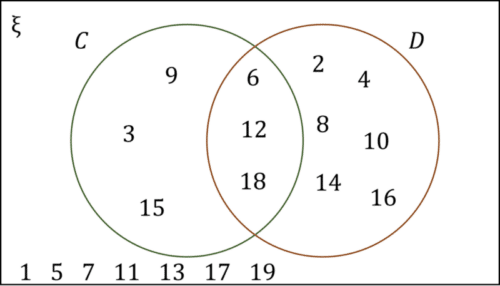
Using the Venn diagram, we can see that
C \cup D=\{2,3,4,6,8,9,10,12,14,15,16,18\}
C \cap D=\{6,12,18\}
All elements that are within the universal set, \xi, but are not contained within either set C or set D are written outside of the circles.
Complement and Subsets
The complement of a set is all the elements of the universal set which aren’t contained within the set. The complement of a set G is written as G'.
Example:
\xi=\{10,11,12,13,14,15,16,17,18,19 \}
G=\{\text{even numbers}\}
The elements of G' are numbers within \xi that are not even, which are 11,13,15,17 and 19
Subsets are sets that are completely contained within another set, so all the elements of the subset are elements of the other set.
A ‘proper subset‘ is defined as a subset which has less elements than the set it is contained within.
The following notation is used for subsets:
A \subseteq B = A is a subset of B
A \nsubseteq B= A isn’t a subset of B
A \subset B= A is a proper subset of B
A \not\subset B= A isn’t a proper subset of B
Example:
\xi=\{\text{positive integers}\}
E=\{\text{positive even numbers}\}
Then we can write E\subseteq \xi
Venn Diagrams – Complements and Subsets

The compliment of a set is represented by everything outside of its corresponding circle on a Venn diagram. For example, \textcolor{#bd0000}{A'} is represented by everything outside of the circle for the set \textcolor{#bd0000}{A}.
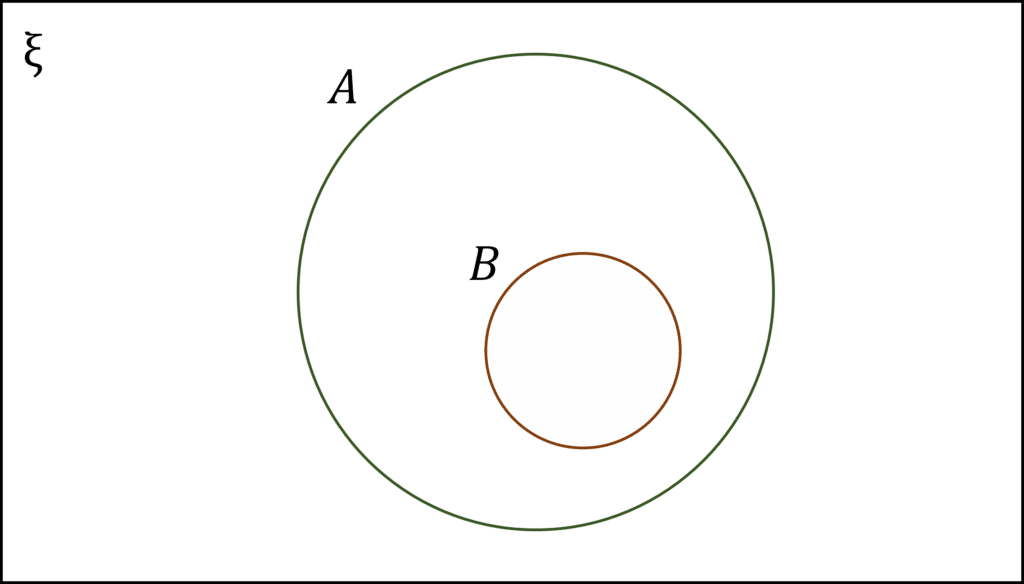
Proper subsets are represented on Venn diagrams by a smaller circle which is completely contained within a larger circle. For example, the diagram on the right shows that \textcolor{#00bfa8}{B} is a proper subset of \textcolor{#00bfa8}{A}.
Example 1: Union and Intersection
Let A=\{3,6,9,12,15,18,21,24,27\} and B=\{2,4,6,8,10,12,14,16,18,20,22,24\}
Write down the elements in
a) A\cup B
b) A \cap B
[2 marks]
a) A \cup B contains elements from at least one of set A or set B.
Therefore, we can write A\cup B=\{2,3,4,6,8,9,10,12,14,15,16,18,20,21,22,24,27\}
Even though 6, 12, 18 and 24 appear in both sets, we only included them once within the set A\cup B
b) A \cap B contains elements that appear in both set A and set B.
Therefore, we can write A\cap B = \{6,12,18,24\}
Example 2: Algebra and Inequality Notation
a) Let \xi=\{\text{positive integers}\} and X=\{x:x<8\}
Write down all the elements within X.
b) Let \xi=\{\text{all 2D coordinates}\} and Y=\{(x,y):y=2x-3\}
Decide whether the following statement is true or false.
(6,8) \in Y[4 marks]
a) We know the universal set is all positive integers, therefore the elements in set X have to be greater than 0.
Thus, the elements within set X must be 1,2,3,4,5,6 and 7
b) For (6,8) to be an element of Y, then x=6 and y=8 would need to satisfy the equation y=2x-3
2(6)-3=9 \neq 8 so therefore (6,8) \in Y is false.
Example 3: Complement and Subsets
Let \xi=\{\text{positive integers less than }20\}, M=\{x:4\leq x \leq 9\}, N=\{\text{Factors of }24\}
a) Find M\cap N'
b) Find (M \cap N)'
c) Let O=\{\text{even numbers}\}
Is (M\cap N) \sub O a true statement?
[6 marks]
a) M=\{4,5,6,7,8,9\} and N=\{1,2,3,4,6,8,12\}
So M\cap N'=\{4,5,6,7,8,9\}\cap \{5,7,9,10,11,13,14,15,16,17,18,19\}=\{5,7,9\}
b) M \cap N= \{4,5,6,7,8,9\} \cap \{1,2,3,4,6,8,12\}=\{4,6,8\}
So (M \cap N)'=\{1,2,3,5,7,9,10,11,12,13,14,15,16,17,18,19\}
c) From b) we have that M \cap N=\{4,6,8\}
Therefore as all the elements of this set are even, (M\cap N) \sub O is true.
Set Notation Example Questions
Question 1: Let \xi=\{\text{negative integers greater than }-20\} and T=\{\text{multiples of }3\}
Write down all the elements that are in the set T.
[2 marks]
The set T can only have elements that are the universal set, so it contains all multiples of 3 greater than -20 and less than 0.
So set T=\{-3,-6,-9,-12,-15,-18\}
Question 2: Let F=\{\text{positive even numbers less than }20\} and G=\{\text{positive multiples of }3\text{ less than }20
Write down the elements in
a) F \cup G
b) F \cap G
[2 marks]
a) The set F\cup G contains all the elements in both F and G.
So F \cup G=\{2,3,4,6,8,9,10,12,14,15,16,18\}
b) The set F\cap G contains the elements that appear in the set F and the set G.
So F\cap G=\{6,12,18\}
Question 3: Let \xi=\{\text{negative integers}\} and N=\{n:n\geq -5\}
Write down all the elements in the set N.
[2 marks]
We know that the universal set is all the negative integers, so all the elements within the set N must be less than 0.
Therefore, set N=\{-5,-4,-3,-2,-1\}
Question 4: Let \xi=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\}, P=\{x:7<x\leq 12\}, Q=\{\text{Multiples of }4\}
a) Find P'\cap Q
b) Let R=\{\text{Factors of }990\}
Show that (P\cap Q')\subseteq R
[5 marks]
a) We know that P=\{8,9,10,11,12\} and Q=\{4,8,12\}
So P'\cap Q=\{1,2,3,4,5,6,7,13,14,15\}\cap \{4,8,12\}=\{4\}
b) R=\{1,2,3,5,6,9,10,11,15\}
P=\{8,9,10,11,12\}
Q'=\{1,2,3,5,6,7,9,10,11,13,14,15\}
So P\cap Q'=\{9,10,11\}, which is a subset of R.
Also, n(P\cap Q')<n(R), which must be true because (P\cap Q')\subseteq R
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.