Inequalities
Inequalities Revision
Inequalities
When we deal with equations, the equals sign tells us that each side of the equation are equal to each other. Another type of equation is an inequality, where the sides of the equation do not equal each other. The inequality sign may tell us one side of the equation is smaller or larger than the other, or smaller than or equal to, or larger than or equal to, each other. You will need to understand how to derive and solve inequalities.
We can also display inequalities on a number line. You will need to understand how to use and interpret inequalities on a number line.
Inequality Symbols
There are 4 symbols used in inequalities, in place of an equals sign in an equation:
- > greater than
Example: 4 > 3 means 4 is greater than 3
- < less than
Example: 3 < 4 means 3 is less than 4
- \geq greater than or equal to
Example: 4\geq4 means 4 is greater than or equal to 4 (6\geq4 is also an example that works)
- \leq less than or equal to
Example: 2\leq3 means 2 is greater than or equal to 2 (3\leq3 is also an example that works)
We often see these sign used in algebraic inequalities:
3x < 4 means 3x is less than 4
Solving Inequalities – Basics
For the most part, we can treat and solve inequalities just as we do with equations (we will talk about the exception later).
Example: solve 3x+3\leq12,
We would treat this as an equation and start by minusing 3 from both sides:
3x\leq9
And now, divide both sides by 3:
x\leq3
Meaning x is less than or equal to 3. This inequality is now solved.
Solving Inequalities with 2 Signs
You may also come across inequalities with 2 signs.
Example:
12<2x+6<24
This means, 2x+6 is between 12 and 24. Or 2x+6 is greater than 12 but less than 24.
We can just as easily solve inequalities like this, in the same way as solving equations, but whatever is done to one side, must be done to all 3 sides:
12<2x+6<24
Start by subtracting 6 from each side to get 2x on its own:
6<2x<18
And then dividing by 2 to get x on its own:
3<x<9
Hence, x is greater than 3 but less than 9
Note: the two signs may not always be the same (for example 12>x\geq2, meaning x is less than 12 but greater than or equal to 2) but these are solved using the same method.
Solving Inequalities: the Exception
There is one case where solving inequalities differs from solving equations, and this occurs when multiplying or dividing by a negative number.
RULE: if you multiply or divide by a negative number, the inequality sign changes direction
When we flip a sign (this means the same as the sign changing direction):
< \rightarrow >\\
> \rightarrow <\\
\leq \rightarrow \geq\\
\geq \rightarrow \leq\\
Example: solve 19<-8x-5<27
Start as usual by adding 5 to each side:
24<-8x<32
Now, we want to isolate the x, so we need to divide by -8 but as we are diving by a negative number, we need to flip the signs to >,
-3 > x > -4
Meaning x is less than -3 but greater than -4
Inequalities on a Number Line
We can display inequalities on a number line.
Note: a filled circle, \bullet is used for the inequalities less than or equal to, and greater than or equal to. Whereas an open circle, \circ, is used for less than or greater than (without the equal to).
Examples:
1.
x>-6
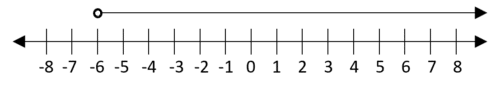
You can see the arrow is pointed towards values greater than -6, because the inequality sign is a greater than, and the circle is open because it is not greater than or equal to.
2.
x\geq-6
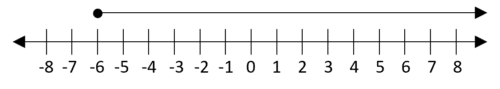
3.
x<6
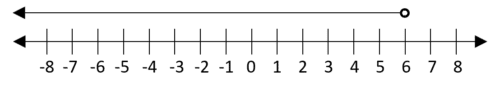
4.
x\leq6
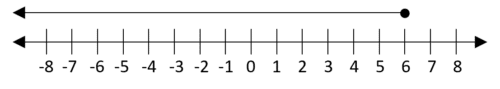
Number lines can also be used for inequalities with 2 signs, for example:
-7<x\leq4
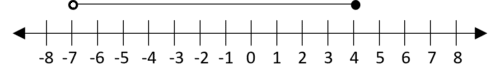
Example 1: Rearranging and Solving Inequalities
Solve the following inequality,
42+x\leq\dfrac{1}{4}x\leq51+x
[3 marks]
Let’s subtract x from each side to get rid of the x‘s on the outside of the inequality:
42\leq-\dfrac{3}{4}x\leq51
Now, let’s divide by -\dfrac{3}{4} to get x on its own. Remember – when dividing by a negative number we need to use the opposite signs:
-56\geq x\geq-68
Example 2: Number Lines
Express the following inequality on a number line,
-3\leq x<5
[2 marks]
So, as the first sign means less than or equal to, the circle on the number line will be filled, but the second sign, less than, will be an empty circle:

Inequalities Example Questions
Question 1: List the integers that satisfy the inequality
-12<x\leq-3
[2 marks]
The values that satisfy this inequality are -11, -10, -9, -8, -7, -6, -5, -4, -3
Question 2: Express the following inequality on a number line
6\geq 2x\geq -4
[3 marks]
Firstly, we need x on its own, so let’s divide by 2,
3\geq x\geq -2
Which can also be written as,
-2\leq x\leq3
And we can plot this on a number line,

Question 3: Solve the following inequality,
-4x+11\leq47
[3 marks]
Start by minusing 11 from each side,
-4x\leq36
Divide through by -4, remembering to flip the sign:
x\geq-9
Question 4: Solve the following inequality,
26-6x\geq2\geq14-6x
[4 marks]
Start by adding 6x to get x in the middle and remove it from the sides,
26\geq2+6x\geq14
Minus 2 from each side,
24\geq6x\geq12
Divide through by 6,
4\geq x\geq2
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.