Finance
Finance Revision
Finance
There are lots of ways maths can help us look at finance problems:
Earnings: Calculating the earning potential of jobs.
Profit and loss: Working out increases and decreases in money.
Discounts: Using percentages and reverse percentages to work out discounts.
Interest and depreciation: Looking at simple and compound interest.
Earnings
Earnings refer to the amount of money someone earns through working a job. This may be given as an hourly rate, or a yearly salary.
Example:
If Sally works 40 hours a week on an hourly wage of £9.40, how much does she earn in a week and what is her yearly salary?
To work out how much Sally earns in a week, we multiply her hourly wage by the number of hours she works per week:
£9.40\times 40 = £376
To work out Sally’s yearly salary, we multiple her weekly wage by the number of weeks in a year, 52:
£376\times 52 = £19552
Profit and Loss
Profit refers to an increase in money, and loss refers to a decrease in money.
It is helpful to look at profit and loss when considering cost and sale prices. For example, a shop owner buys products to sell in their shop and this is a cost, and then sells these products, which is a sale.
Example:
A shop owner buys 100 teddy bears to sell in their shop, and they each cost £2.80. The shop owner sells each of these for £6.99 in their shop. They only managed to sell 48 teddy bears in their shop.
Work out whether they made a profit or a loss, and the amount of profit or loss.
To work out profit and loss, we need to find the difference between costs and sales.
Costs: 100\times £2.80 = £280
Sales: 48\times £6.99 = £335.52
As the sales were higher than the costs, the shop owner has made a profit. The amount of profit is the sales minus the costs:
£335.52 - £280 = £55.52
Discounts
When a shop reduces the price of a product, the product is discounted.
Discounts are often written as percentages, for example, a shop may discount a product by 25\%.
Example:
A dress usually costs £25. The dress goes on sale with a 30\% discount. Calculate the sale price of the dress.
We use our knowledge of percentages to calculate this. If a dress has a 30\% discount, it will be 70% of the original price:
£25\times0.7=£17.50
We may be given a sale price and asked to calculate the discount.
Example:
A dress usually costs £48 and goes on sale for £26.40, calculate the percentage discount.
Here, we use reverse percentages. We know that £48 multiplied by 1 - the discount would equal £26.40, so we can do the opposite to find the discount:
£26.40\div£48=0.55So the sale price is 55\% of the normal price, meaning the discount is 45\%.
Interest and Depreciation – Simple
Simple interest is where we increase a value by the same percentage repeatedly. This means the interest is only on the original amount and not on the interest over time.
Example
A bank account contains £5000 and gets 5\% simple interest each year. Calculate the amount in the bank account after 3 years.
Find 5\% of £5000:
£5000\times0.05 = £250Therefore, each year this bank account will increase by £250:
£5000 + £250 + £250 + £250 = £5750 after 3 years.
Interest and Depreciation – Compound
Unlike simple interest, compound interest means you get interest on your interest. The following formula enables you to calculate the compound interest or depreciation:
\textcolor{purple}{N} = \textcolor{blue}{N_0} \, \times \bigg( 1 \textcolor{red}{\pm \dfrac{\text{Percentage}}{\text{100}}} \bigg) ^{\textcolor{orange}{n}}
\textcolor{purple}{N} = \text{\textcolor{purple}{Amount after the period of time}}
\textcolor{blue}{N_0} = \text{\textcolor{blue}{The original amount}}
\textcolor{red}{+} \, \text{\textcolor{red}{when it is growth}} ; \textcolor{red}{-} \, \text{\textcolor{red}{when it is decay}}
\textcolor{orange}{n} = \text{\textcolor{orange}{Number of periods}} \text{\textcolor{orange}{(days/hours/minutes etc.)}}
Example
A bank account contains £5000 and gets 5\% compound interest each year. Calculate the amount in the bank account after 3 years.
Year 1:
\textcolor{red}{5\%} on top of 5000 = \textcolor{limegreen}{£5250}.
Year 2:
\textcolor{red}{5\%} on top of 5250 = \textcolor{limegreen}{£5512.50}.
And so on …
To find compound growth after \textcolor{orange}{n} years, we can substitute all the values into the compound growth and decay formula:
Here \textcolor{Orange}{n = 3}
\textcolor{purple}{N} = \textcolor{blue}{£5000} \times \bigg(1 \textcolor{red}{+ \dfrac{5}{100}} \bigg) ^{\textcolor{orange}{3}} = \textcolor{purple}{£5788.13} (2 dp)
This formula works in the same way for decay, but using 1 - \dfrac{\text{Percentage}}{100}.
Example 1: Using Data from a Table
Holly is 22 years old and is looking for a new marketing job. She wants to earn at least £12 an hour. She has 2 years marketing experience and gets an interview at ‘Marketing 4 U’. They send her information about their salaries for employees working 40 hours per week:
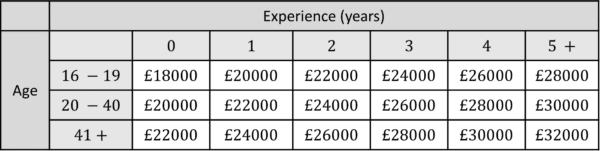
Calculate whether Holly would make the amount of money she wants if she took this job.
[3 marks]
We know Holly is 22 with 2 years experience, so her salary would be £24000. We need to work out what her hourly rate is. Firstly, work out how much she would earn per week:
£24000\div52=£461.54And then per hour:
£461.54\div40=£11.54
Therefore, Holly would earn less than £12 an hour.
Example 2: Compound Depreciation
A car purchased for £4500 depreciates by 8\% each year.
Calculate the value of the car after 6 years.
[3 marks]
We can use the formula we learnt earlier to answer this question:
Here \textcolor{Orange}{n = 6}
\textcolor{purple}{N} = \textcolor{blue}{£4500} \times \bigg(1 \textcolor{red}{- \dfrac{8}{100}} \bigg) ^{\textcolor{orange}{6}} = \textcolor{purple}{£2728.60} (2 dp)
Finance Example Questions
Question 1: Alice is running a bake sale. She buys ingredients for 140 cakes, and the cost for one is 56\text{ p}.
Alice manages to sell 75 cakes for 99\text{ p} each.
Calculate whether Alice made a profit or a loss, and the amount of the profit or loss.
[3 marks]
Costs: £0.56\times 140=£78.40
Sales: £0.99\times 75=£74.25
The costs were higher than the sales, so Alice made a loss.
The loss amount:
£78.40-£74.25=£4.15Question 2: Alana buys a t-shirt and a skirt. They are both on sale. The t-shirt was originally £12 and was discounted by 25\%, and the skirt was on sale for 8\% less than its original price.
In total, Alana spent £29.24 on the t-shirt and skirt.
Calculate the original price of the skirt before it went on sale.
[4 marks]
Total spend: £29.24
T-shirt sale price: £12\times 0.75 =£9
Skirt sale price: £29.24-£9=£20.24
Skirt original price: £20.24\div0.92=£22
Question 3: A house purchased for £105,000 increases in value by 2\% each year.
Find the value of the house after 5 years to the nearest pound.
[4 marks]
So, each year the price is multiplied by 1.02.
We can now put these values into the formula to find the value of the house after 5 years:
£105000\times 1.02^5=£115928 to the nearest pound.






