Equations of Straight Lines
Equations of Straight Lines Revision
Equations of Straight Lines
Straight line equations are a rule for generating straight lines on an x–y plane.
Every equation for a straight line takes the same form:
y=mx+c
Where y and x are the variables and m and c are constants that define the straight line.
The Equation
y=mx+c
x & y are the Cartesian coordinates. These are graphed into an x-axis and a y-axis, that shows how y varies as the input of x changes. If y=4 when x=3 we would write this coordinate as (3, 4) (the x coordinate always goes first).
m is the gradient of the line. Which can be found from two points on the line. If (x_1, y_1) and (x_2, y_2) are points on the straight line then,
m=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}
Where \Delta x means the change in x (in this case between x_2 and x_1).
For more on gradient, see here our section on gradients
c is known as the y-intercept. It is the value of y when x=0. So the point (0,c) is on the line, and is where the line crosses the y-axis. c can be found if you have the gradient m and a point on the line (x_1, y_1).
c =y_1 - mx_1
Graphical Interpretation
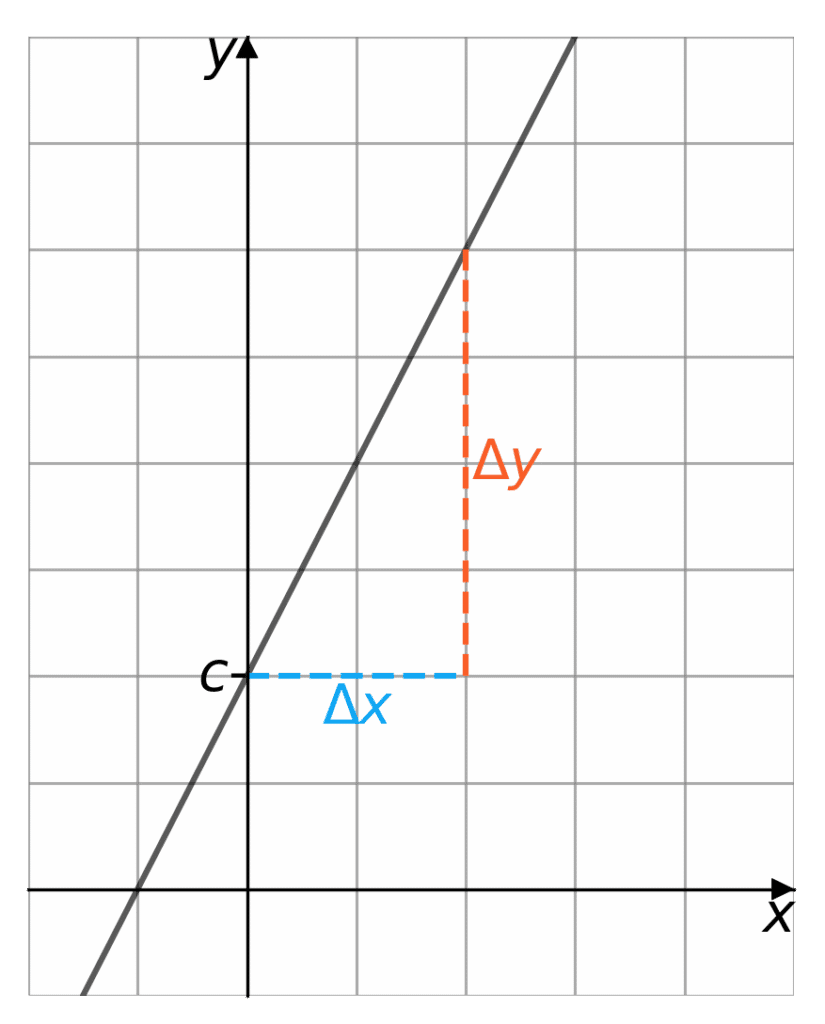
When a straight line has been graphed the equation can be deduced. Where the line crosses the y-axis is the y-intercept, c. You can then pick two points on the line and find the difference in y and the difference in x between the points. When the line is drawn on a graph, you can pick the points for ease of calculation.
So if the line passes through (x_1,y_1) and (x_2,y_2) then m = \dfrac{y_1-y_2}{x_1-x_2}
You may see on the graph, that for every 1 unit x increases, y increases by m units.
Remember if y decreases as x increases then the gradient is going to be negative.
Example 1: Deriving the Equation From a Graph
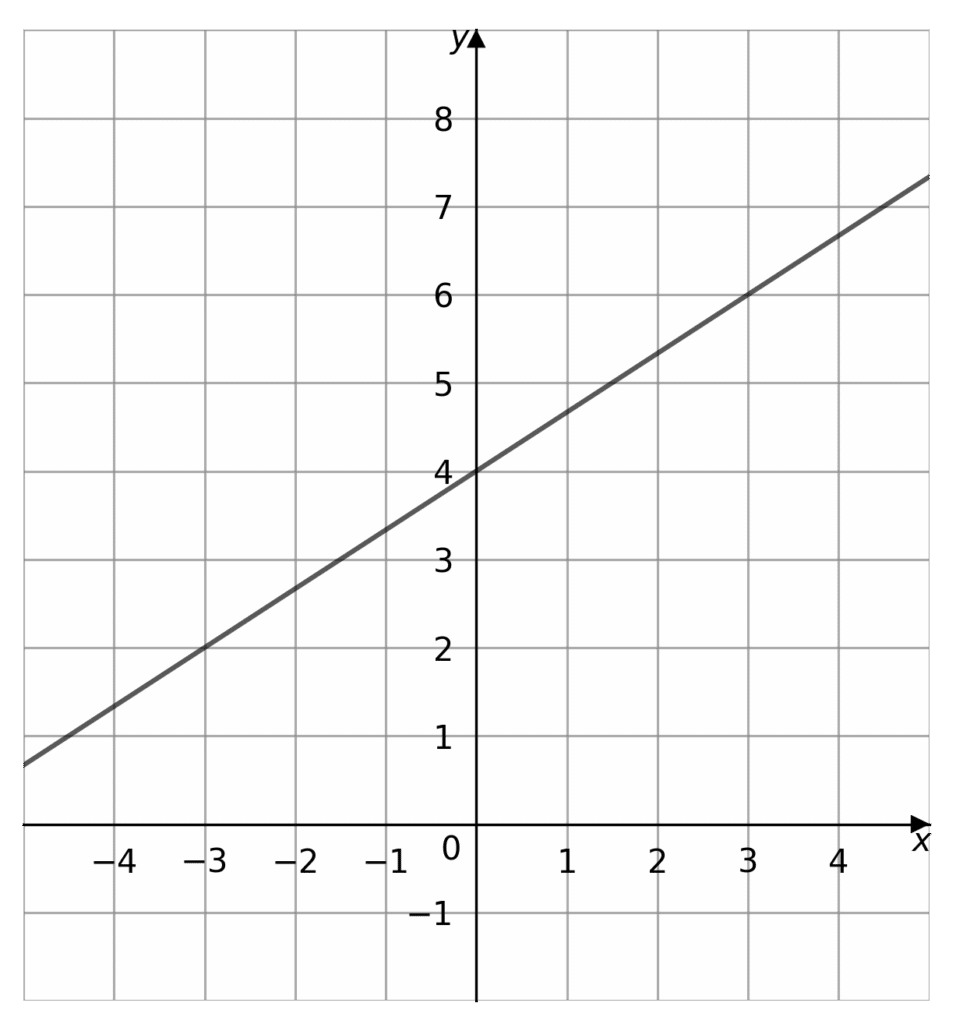
From the graph given, we want to derive an equation for the straight line.
[3 marks]
The graph crosses the y-axis at the point (0,4), so the y-intercept, c, is equal to 4. We must now find another point to find the gradient.
Looking at another point, let’s choose (3,6) we can find the gradient.
\Delta y = 6-4=2
\Delta x = 3-0 so,
m=\dfrac{2}{3}
Then the equation for the straight line is
y=\dfrac{2}{3} x+4
Example 2: Straight Lines Between Two Points
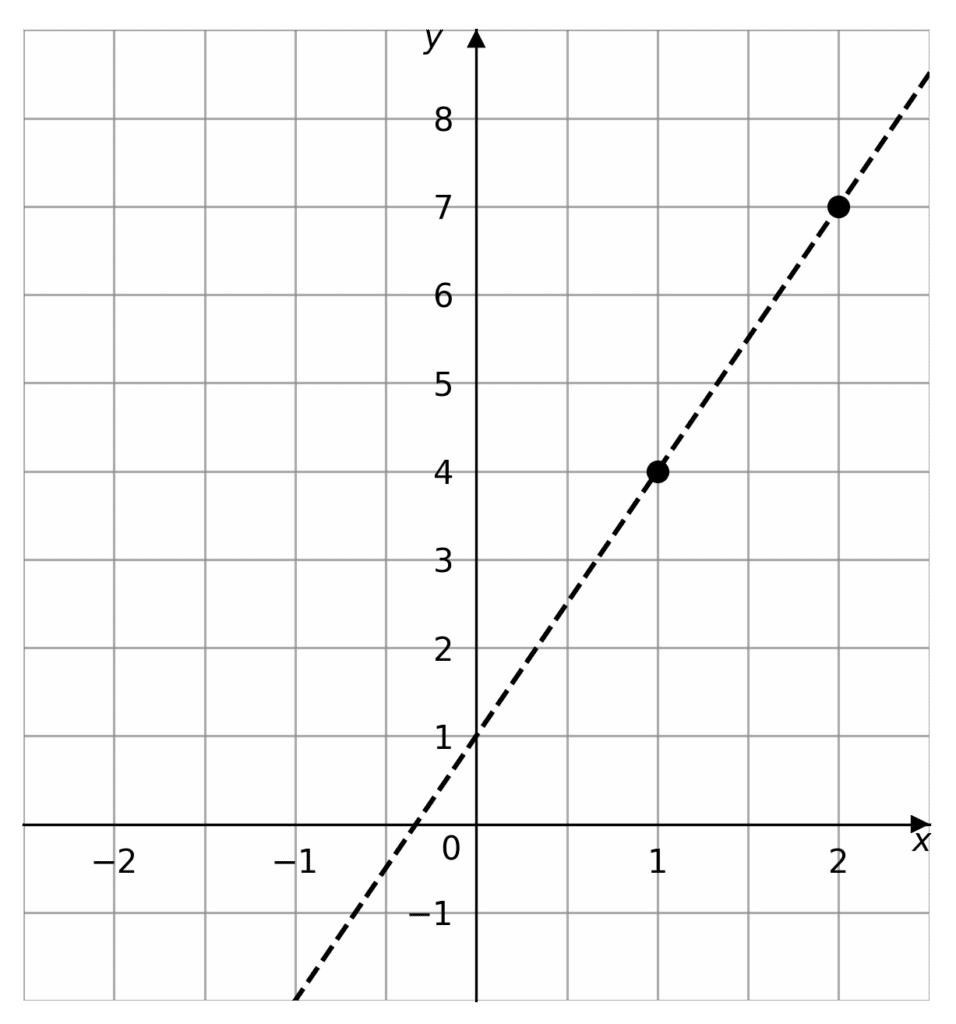
Any two points on the coordinate plane can be connected by a straight line. So we must be able to find an equation for this straight line. So lets find the equation to the line that passes through (1, 4) and (2, 7).
[3 marks]
Firstly we must find the gradient, as we cannot find the y-intercept without it.
\Delta y = 7-4 = 3
\Delta x = 2-1 = 1, so
m=\dfrac{3}{1}=3
Now we have y=3x+c, so what we can do is substitute one of our points on the graph into the equation to find c, we shall choose (1,4) although it doesn’t matter which one.
y=3x+c \rightarrow 4=3 \times 1 +c
4-3=c
c=1
So the equation is y=3x + 1
Equations of Straight Lines Example Questions
Question 1: Given the following graph:
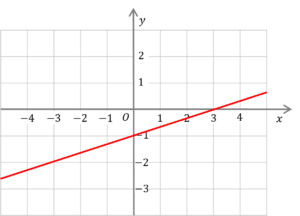
What is the equation for the red line?
[3 marks]
Straight line equations take the form y=mx+c
We can clearly see that the red line crosses the y-axis at the point (0,-1), so c=-1
Taking another point on the line, choose (3,0) we shall find m.
m = \dfrac{\Delta y}{\Delta x} = \dfrac{-1-0}{0-3}= \dfrac{1}{3}
So the equation for the red line is
y=\dfrac{1}{3}x-1
Question 2: A straight line has the equation 2x=\dfrac{y}{2}-4
a) Find the gradient of this line.
[2 marks]
b) Find the point this line crosses the x-axis.
[1 mark]
a) We need to put this equation into the form y=mx +c
2x=\dfrac{y}{2}-4
4x=y-8
y=4x+8
So the gradient is 8
b) The point that the line crosses the x-axis is when y=0, so
2x=\dfrac{0}{2} -4
2x=-4
x=-2
The line crosses the x-axis at the point (-2,0)
Question 3: Give the equation for the straight line that passes through the points (3,3) and (6,0)
[3 marks]
First, we shall find the gradient of the line that passes through (3,3) and (6,0).
m=\dfrac{\Delta y}{\Delta x}
\Delta y = 0-3= -3
\Delta x = 6-3=3
So
m=\dfrac{-3}{3}=-1.
To find c we shall substitute in the coordinates (3,3).
3= (-1)\times 3 + c
c= 3+3 = 6
The equation for the straight line is y=-x+6
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.