Coordinates and Midpoints
Coordinates and Midpoints Revision
Coordinates and Midpoints
The Cartesian coordinates are a coordinate system that is in made up of two axes, the x-axis and the y-axis. As such each point on the x–y plane has an x-coordinate and a y-coordinate, that places the point in the 2\text{D} space.
Midpoints are the halfway points between two points. So if A and C are points on the x–y plane, then we can define a point B exactly half way between them. So that the distance between A and B is the same as the distance between B and C.
Cartesian Coordinates
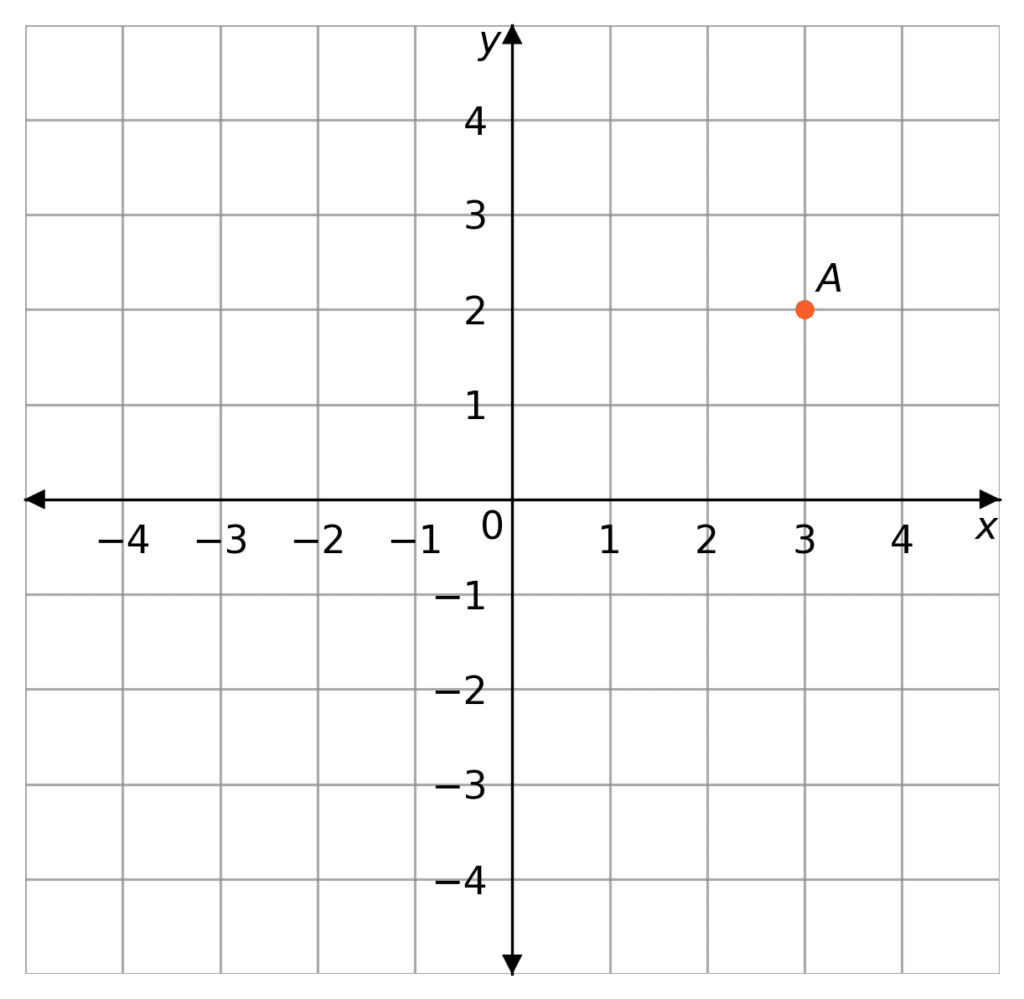
For a point A the Cartesian coordinates of A can be given as
(A_x, A_y),
where A_x is the x-coordinate and A_y is the y-coordinate. The x-coordinate always is written first (just remember x comes before y in the alphabet).
We call the point with coordinates (0,0) the origin, denoted O.
So if point A has the coordinates (3,2), that means that, from the origin, the point lies 3 units to the right (the x-axis) and 2 units up (the y-axis), as shown.
Distance Between Points
One of the many useful things about Cartesian coordinates, is the ease at which we can find the precise distance between any two points.
Let point A = (x_1, y_1) and point B = (x_2, y_2). What we can do, between these two points, is construct a right angled triangle. The vertices of this triangle will be A, B and the point (x_2, y_1). Then to find the distance from A to B we can find the base of the triangle and the height of the triangle.
The base of this triangle is A to (x_2, y_1). As they have the same y-coordinate, the base of this triangle is
\text{Base}= x_2-x_1.
Similarly, the height of the triangle is from (x_2, y_1) to B. As they have the same x-coordinate, the height of this triangle is
\text{Height}=y_2-y_1.
Now, we can just use the Pythagorean theorem, as we have constructed a right angle triangle,
\text{Distance }AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2},
as the distance between A and B, is just the length of the hypotenuse of the triangle.
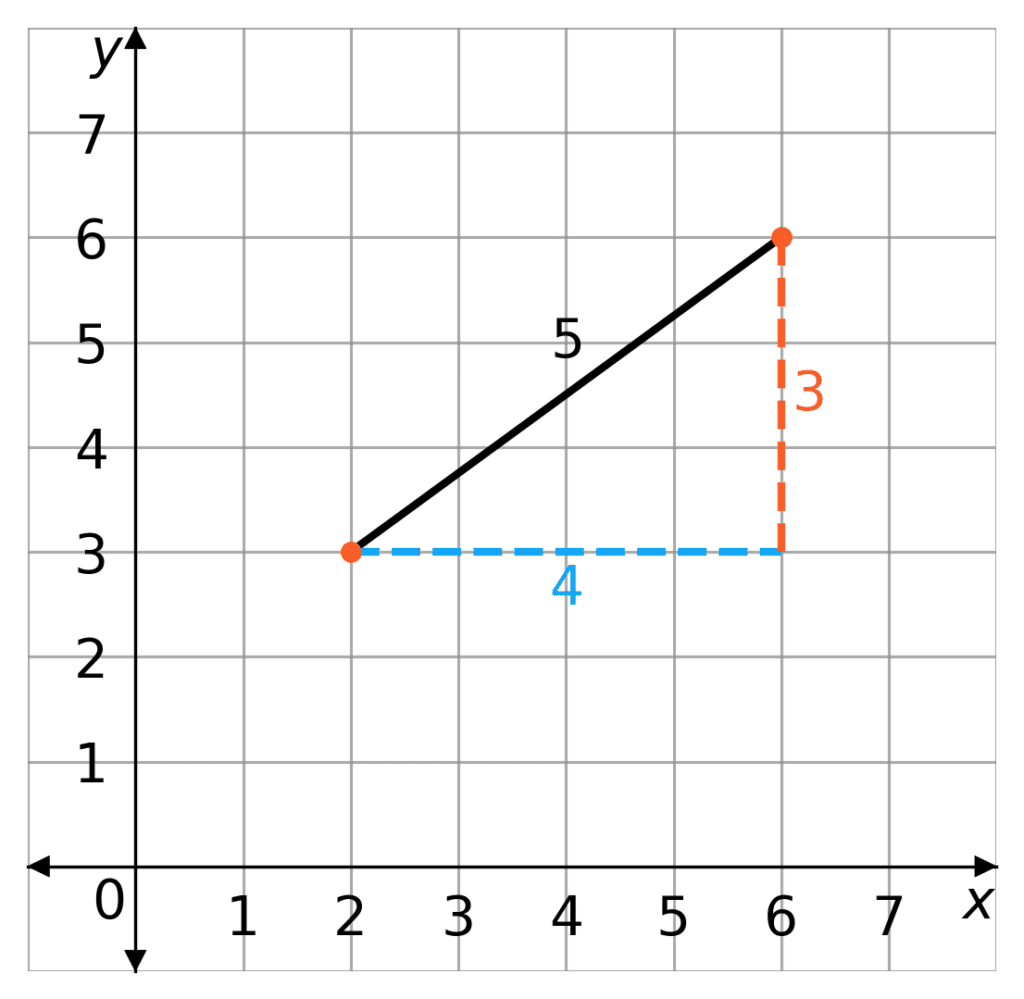
For our example here, the points are (2,3) and (6,6), so the base of out triangle is
\text{Base}= 6 - 2 = 4
the height is
\text{Height} =6 - 3= 3
and so by Pythagoras, the distance between the points is
\text{Distance between points }= \sqrt{4^2+3^2}= 5
Midpoints
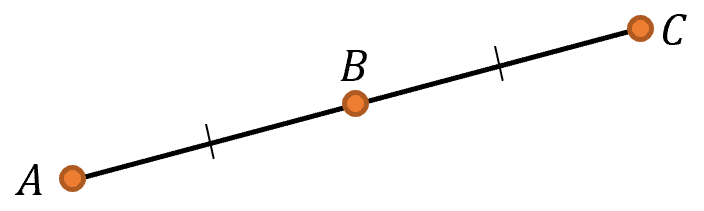
Midpoints are the points that lie directly in the middle of two other points. Let’s say that B is the midpoint of A and C. Then if there is a straight line between A and C then the point B bisects the line.
If A has the coordinates (x_1, y_1) and point C has coordinates (x_2, y_2) then the midpoint is
\text{Midpoint} = \left( \dfrac{x_1+x_2}{2}, \dfrac{y_1 + y_2}{2} \right) .
We can think of the midpoint as the average point between A and C
The distance to the midpoint is, intuitively
\text{Distance }AB=\dfrac{1}{2} \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} =\text{Distance }BC
or
\text{Distance }AB=\sqrt{ \left( x_1 - \dfrac{x_2+x_1}{2}\right)^2+\left( y_1- \dfrac{y_2+y_1}{2}\right)^2} =\text{Distance }BC
Example 1: Finding a Midpoint
Find the midpoint between the points (3,8) and (15, 16)
[2 marks]
The midpoint
\text{Midpoint}= \left( \dfrac{3+15}{2}, \dfrac{8+16}{2} \right) = (9, 12)
Example 2: Finding the Distance Between Two Points
Find the distance between the points (17,9) and (11,17)
[2 marks]
Using Pythagoras for Cartesian coordinates
\text{Distance}= \sqrt{(17-11)^2+(9-17)^2},
\text{Distance}= \sqrt{(6)^2+(-8)^2}= \sqrt{36+64},
\text{Distance}= \sqrt{100}=10.
The distance cannot be -10, as distance is a positive value.
Example 3: Finding the Distance To a Midpoint
Find the midpoint between the points (5,6) and (13,14), and the distance between (5,6) and the midpoint.
[4 marks]
The midpoint
\text{Midpoint}= \left( \dfrac{5+13}{2}, \dfrac{6+14}{2} \right) = (9, 10)
Using Pythagoras for Cartesian coordinates
\text{Distance}= \sqrt{(9-5)^2+(10-6)^2},
\text{Distance}= \sqrt{(4)^2+(4)^2}= 4\sqrt{2}.
The distance cannot be - 4\sqrt{2}, as distance is a positive value.
Coordinates and Midpoints Example Questions
Question 1: Find the distance between the points (5, 12) and (60,60)
[2 marks]
We use Pythagoras’s theorem for Cartesian products.
\text{Distance}= \sqrt{(60-5)^2+(60-12)^2}
\text{Distance}= \sqrt{55^2+48^2}
\text{Distance}= \sqrt{3025+2304}= \sqrt{5329}=73
The distance between the two points is 73
Question 2: Find the midpoint between the points (4, 16) and (24,-16)
[2 marks]
The midpoint is
\text{Midpoint}= \left( \dfrac{4+24}{2}, \dfrac{16+ (-16)}{2} \right)
\text{Midpoint}= (14,0)Question 3: Points A and B have a midpoint at (11, 43). Given that point A has coordinates (2,3)
a) Find the coordinates of point B.
[3 marks]
b) Find the distance between point A and point B.
[2 marks]
a) Let B = (b_x, b_y). Then we have
(11,43) = \left( \dfrac{2+b_x}{2}, \dfrac{3+b_y}{2} \right)
So for b_x,
11 = \dfrac{2+b_x}{2}
22 = 2+b_x
b_x=20.
For b_y,
43 = \dfrac{3+b_y}{2}
86 = 3 + b_y
b_y = 83
So B= (20, 83)
b) Using Pythagoras’s theorem for Cartesian products.
\text{Distance}= \sqrt{(20-2)^2+(83-3)^2}
\text{Distance}= \sqrt{18^2+80^2}
\text{Distance}= \sqrt{324+6400}= \sqrt(6724)=82
The distance between the two points is 82







