Circle Theorems and Angles
Circle Theorems and Angles Revision
Circle Theorems
Circle theorems are properties of circles that allow us to consider and work out angles within the geometry of a circle.
You need to be able to identify, utilise, and describe each theorem.
Rule 1 – Angles in a Semicircle
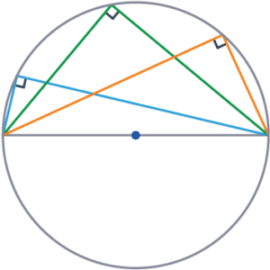
The angle extended from the diameter is always a right angle.
This may be written as ‘a diameter subtends a right-angle at the circumference’.
Rule 2 – Tangent/Radius Angle
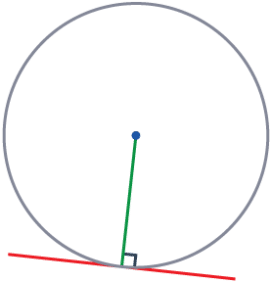
The angle where a tangent meets a radius is always a right angle.
This may be written as ‘the tangent and radius that meet are perpendicular’.
Rule 3 – Segment Angles
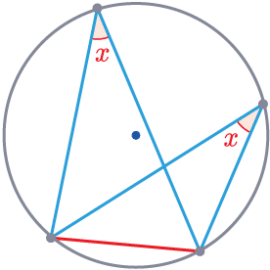
Angles drawn from the same chord are equal when touching the circumference.
The lines may or may not pass through the centre.
Rule 4 – Centre Angle

The angle at the centre is twice the size of the angle at the circumference.
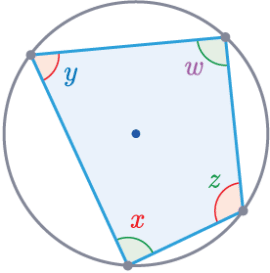
Rule 5 – Cyclic Quadrilateral
A cyclic quadrilateral is a four-sided shape within a circle, with each corner touching the circumference.
In a cyclic quadrilateral, opposite angles add to 180\degree.
\textcolor{purple}{w}+\textcolor{red}{x}=180\degree
\textcolor{blue}{y}+\textcolor{limegreen}{z}=180\degree
Rule 6 – Alternate Segment Theory
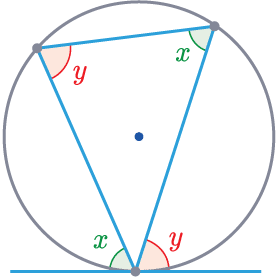
The angle between the tangent to the circle and the side of the triangle is equal to the opposite interior angle. This is the same for the angle on the other side of the tangent:
\textcolor{limegreen}{x}=\textcolor{limegreen}{x}
\textcolor{red}{y}=\textcolor{red}{y}
Rule 7 – Tangents from the Same Point
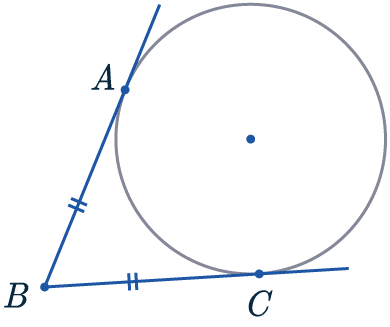
Tangents from the same point to the circumference are equal in length:
AB = BC
Rule 8 – Perpendicular Bisector of a Chord
The perpendicular bisector to a chord will always pass through the centre of the circle.
This can be any length chord anywhere in the circle.
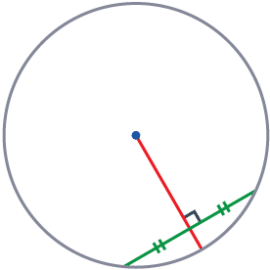
Rule 9 – Equal Chords are Equidistant from the Centre
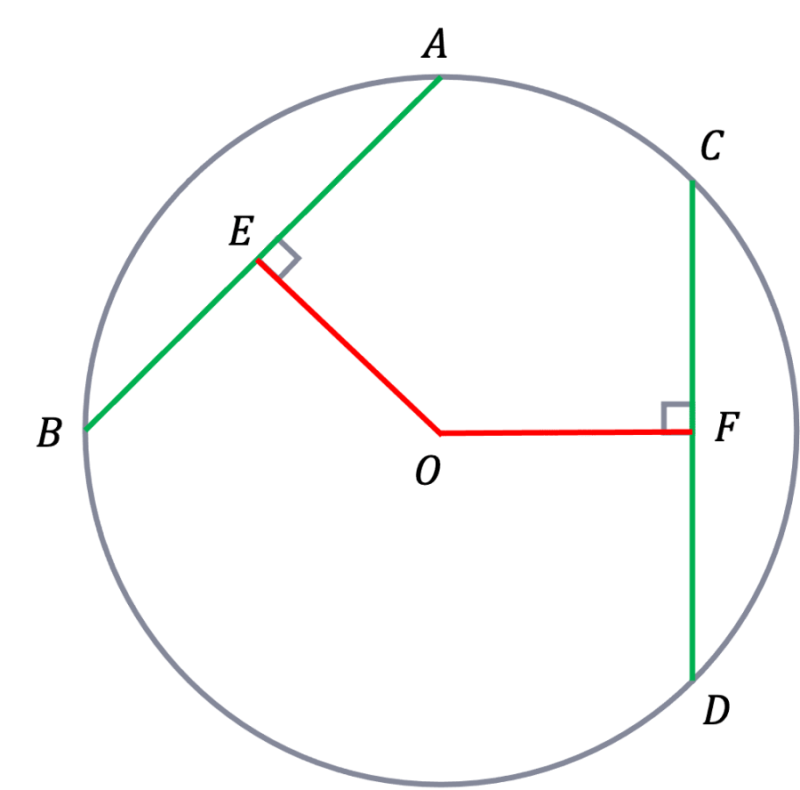
Chords of equal length of a circle are equidistant from the centre.
Taking a look at the diagram to the left.
AB=CD and are both chords of the same circle.
This means they are both equal distance from the centre
Therefore EO=OF
Example 1: Using Circle Theorems
Use one of the circle theorems to calculate the size of angles x and y.
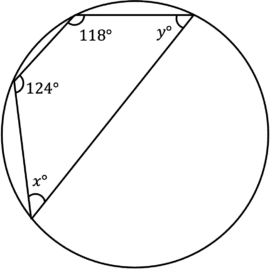
[3 marks]
We can use rule 5 – this is a cyclic quadrilateral, so the opposite angles add to 180\degree.
So x and 118 add to 180,
180 - 118 = x\\ x = 62\degree\\
And y and 124 add to 180,
180 - 124 = y\\ y = 56\degree\\Example 2: Using Multiple Theorems
The line AC passes through the centre of the circle.
Use circle theorems to work out the angles x\degree and y\degree
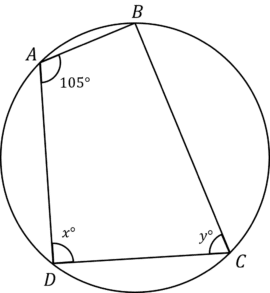
[3 marks]
Firstly, we can use rule 5, this is a cyclic quadrilateral, so opposite angles add to 180\degree
We can use this to work out y,
180-105=75\degree\\ y=75
Now, we can use rule 1 – as AC passes through the centre, this is a diameter of the circle, so the angle that extends from the diameter is a right angle. Therefore, B and D are right angles, so,
x=90
Circle Theorems and Angles Example Questions
Question 1: AB is a tangent to the circle at point D. BC is a tangent to the circle at point E.
Given that length BD is 6\text{ cm}, work out the length BE.
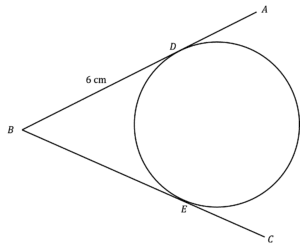
[2 marks]
We know from rule 7 that tangents from the same point are the same length, so BE is also 6\text{ cm}
Question 2: Work out the size of angles x and y.

[2 marks]
Using rule 3, we know angles from the same chord are equal when touching the circumference. So:
x=16\degree\\ y=22\degree\\Question 3: Given that line BG is the perpendicular bisector of AC and EI is the perpendicular bisector to DF, work out the size of angle x.
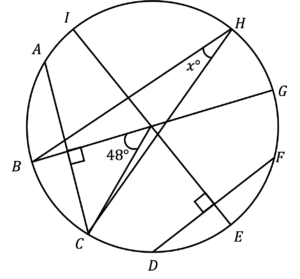
[4 marks]
We know that perpendicular bisectors to chords pass through the centre (rule 8), so the point where EI and BG cross must be the centre of the circle.
This means we can use rule 4, as we have an angle at the centre and an angle at the circumference. Using this rule, we know x will be half the size of 48, and hence, is 24\degree.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.