Revise
Arc Length and Sector Area
Arc Length and Sector Area Revision
Arc Length and Sector Area
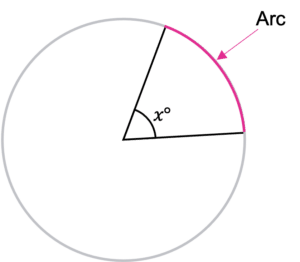
An arc is part of the circumference of a circle, and you will need to know how to calculate the length of an arc based on the angle at the centre of the circle.
A sector a section of a circle, with the edges being two radii and an arc. You will need to know how to calculate the area of a sector.
Arc Length
Arc length can be calculated using the following equation:
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
Remember:
Circumference of a circle =\pi d
Where d is the diameter
Sector Area
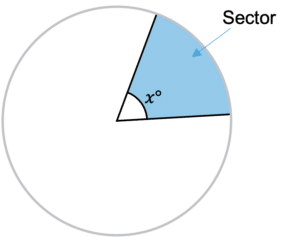
Sector area can be calculated using the following equation:
Area of Sector = \dfrac{x}{360}\times Area of full Circle
Remember:
Area of a circle = \pi r^2
Where r is the radius
Example 1: Arc Length in terms of \pi
Find the length of the following arc, giving your answer in its exact form.
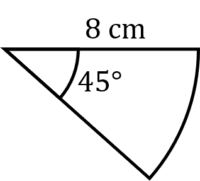
[3 marks]
When a question asks for an answer in its exact form, we can give the answer in terms of \pi.
Firstly, we need to find the overall circumference of the circle that the arc is part of.
The equation for the circumference of a circle is:
Circumference = \pi d
As the radius is 8\text{ cm}, the diameter is 16\text{ cm}, so the circumference is 16\pi
We can now work out the length of the arc:
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
Length of Arc = \dfrac{45}{360}\times16\pi
Length of Arc = 2\pi\text{ cm}
Example 2: Sector Area in terms of \pi
Find the area of the following sector, giving your answer in its exact form.
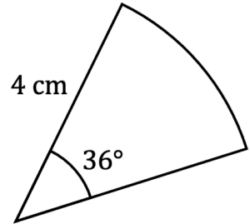
[3 marks]
Firstly, we need to find the overall area of the circle that the sector is part of.
The equation for the area of a circle is:
Area = \pi r^2
AS r=4 \rightarrow Area = \pi\times4^2 = 16\pi\text{ cm}^2
We can now work out the area of the sector:
Area of Sector = \dfrac{x}{360}\times Area of full Circle
Area of Sector = \dfrac{36}{360}\times16\pi
Area of Sector = \dfrac{8}{5}\pi\text{ cm}^2
Example 3: Arc Length
Find the length of the following arc to 3 significant figures.
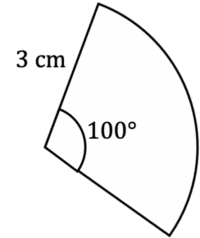
[3 marks]
Firstly, we need to find the overall circumference of the circle that the arc is part of.
The equation for the circumference of a circle is:
Circumference = \pi d
As the radius is 3\text{ cm}, the diameter is 6\text{ cm}, so the circumference is 6\pi
We can now work out the length of the arc:
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
Length of Arc = \dfrac{100}{360}\times6\pi
Length of Arc = 5.24\text{ cm}
Arc Length and Sector Area Example Questions
Question 1: Find the length of the following arc, giving your answer in exact form.
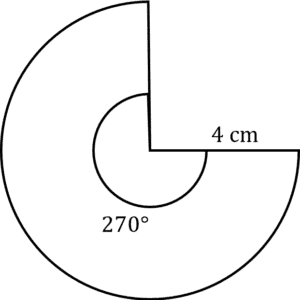
[3 marks]
Firstly, find the circumference,
Circumference = \pi d
Circumference = 8\pi
And now, the length of the arc,
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
Length of Arc = \dfrac{270}{360}\times8\pi
Length of Arc = 6\pi\text{ cm}
Question 1: Find the area of the sector, to 2 decimal places.
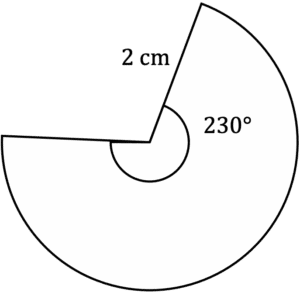
[3 marks]
Find the area of the full circle:
=\pi\times2^2 =4\pi
Area of the sector:
=\dfrac{230}{360}\times4\pi =8.03\text{ cm}^2Question 2: Find the perimeter of the following shape to the nearest whole number.
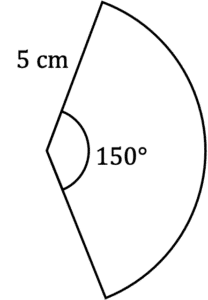
[4 marks]
Firstly, let’s find the length of the arc.
Length of full circle circumference:
=10\piLength of arc:
=\dfrac{150}{360}\times 10\pi =\dfrac{25}{6}\pi
Total perimeter also includes the two radii:
\dfrac{25}{6}\pi+5+5=23\text{ cm} (to the nearest whole number)
Question 3: A sector, with an angle of 72\degree, has an area of \dfrac{36}{5}\pi. Calculate the radius of the circle.
[4 marks]
Working backwards, the equation is:
\dfrac{36}{5}\pi=\dfrac{72}{360}\times \pi r^2Cancel out the pi’s:
\dfrac{36}{5}=\dfrac{72}{360}\times r^2Divide through by \dfrac{72}{360}:
36=r^2r=6 (we can ignore the negative root as lengths are always positive)
