Revise
3D Symmetry
3D Symmetry Revision
3D Symmetry
Similarly to 2D shapes, some 3D shapes are also symmetrical. Rather than having lines of symmetry, 3D shapes have planes of symmetry. A plane of symmetry occurs if you can cut the shape into two halves, the halves are mirror images of each other.
We will look at the 3D symmetry of cylinders, prisms, and pyramids.
Cylinders
Cylinders have circular symmetry, meaning they have an infinite number of planes of symmetry.
They have one plane of symmetry across the curved face:
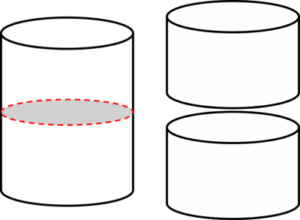
If the cylinder is cut in half at this plane of symmetry, it produces two shapes that are mirror images of eachother.
Cylinders have circular symmetry with planes of symmetry such as the following:
These planes of symmetry can be infinitely rotated, giving an infinite number of planes of symmetry.
Prisms
Regular triangular prisms have 4 planes of symmetry.
They have one plane of symmetry across the rectangular face:
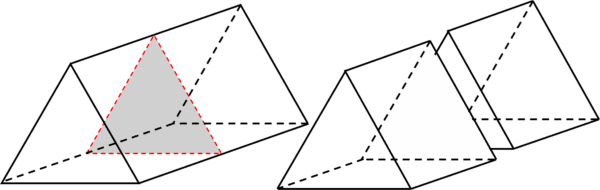
And they have 3 planes of symmetry as following:
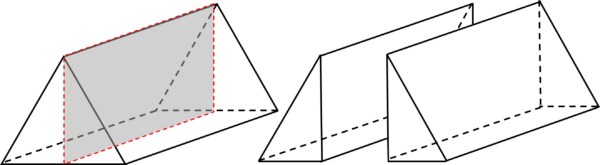
This plane of symmetry can be from any of the 3 vertices, giving the shape a total of 4 planes of symmetry.
For other prisms, it is useful to draw or visualise the shape and identify the planes of symmetry.
Pyramids
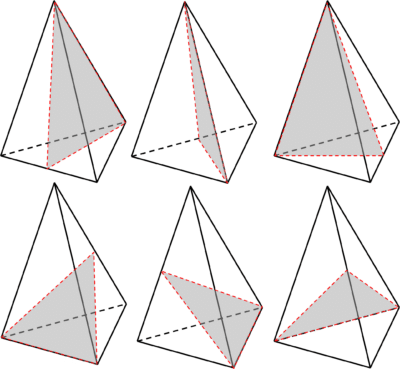
Square based pyramids have 4 planes of symmetry, as shown below:
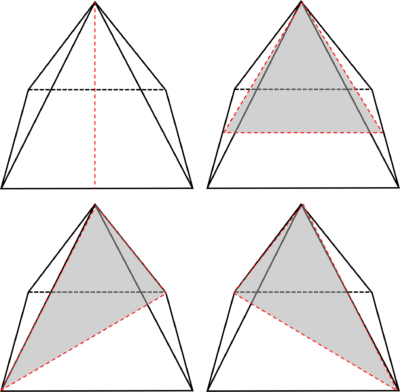
Regular triangular based pyramids have up to 6 planes of symmetry, as shown below:
3D Symmetry Example Questions
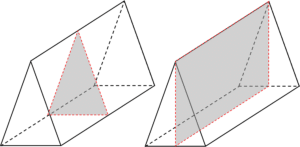
Question 1: State the number of planes of symmetry in an isosceles triangular prism.
[2 marks]
Question 2: State the number of planes of symmetry in a sphere.
[2 marks]
A sphere contains infinitely many planes of symmetry.
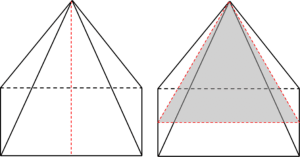
Question 3: State the number of planes of symmetry in a rectangular-based pyramid.
[2 marks]
