3D Pythagoras and Trigonometry

GCSELevel 6-7AQACambridge iGCSEEdexcelEdexcel iGCSEOCRWJEC

3D Pythagoras and Trigonometry Revision

3D Pythagoras and Trigonometry

$3D$ Pythagoras and Trigonometry is just adding a $3$ rd dimension.

First lets recap the basics.

Pythagoras’ Theorem.

$\textcolor{red}{a}^2 + \textcolor{limegreen}{b}^2 = \textcolor{blue}{c}^2$ ,

Secondly, trigonometry and SOHCAHTOA.

$\sin(x) = \dfrac{O}{H}, \,\, \cos(x) = \dfrac{A}{H}, \,\, \tan(x) = \dfrac{O}{A}$

Make sure you are happy with these topics before continuing

– Revise trigonometry

– Revise Pythagoras

3D Pythagoras

For $3D$ Pythagoras, there is a new equation we can use, which just uses Pythagoras’ theorem twice.

In the diagram shown, find the length of $\textcolor{red}{d}$

[3 marks]

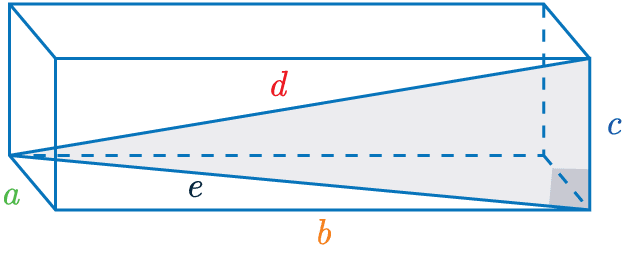
We already know that,

Equation $1$ :

$\textcolor{limegreen}{a}^2 + \textcolor{orange}{b}^2 = \textcolor{black}{e}^2$

and we can see that $edc$ also forms a right angled triangle so we know,

Equation $2$ :

$\textcolor{black}{e}^2 + \textcolor{blue}{c}^2 =\textcolor{red}{d}^2$

So this means we can combine equation $1$ and $2$ , to give our $3D$ Pythagoras equation.

$\textcolor{limegreen}{a}^2 + \textcolor{orange}{b}^2 +\textcolor{blue}{c}^2 =\textcolor{red}{d}^2$

3D Trigonometry

With $3D$ Trigonometry, there is no trick, you need to solve each section in steps which makes it a harder topic.

Example: Shape $ABCDEFG$ is a cuboid.

[3 marks]

Find the length of side $FC$ , marked in red, to $3$ sf.

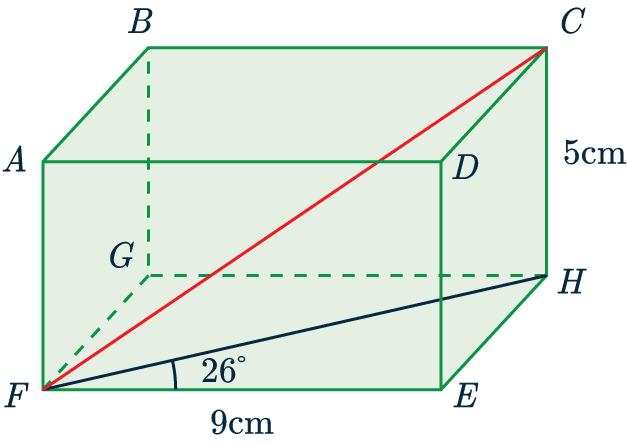
Firstly, the shape is a cuboid, which means every corner is a right-angle.

First what we need to do is find $FH$ , this will give us the base of the right-angled triangle $FHC$ , which will let us find $FC.$

To find side-length $FH$ , we need to use trigonometry

Adjacent $FE=9\text{ cm}$

Hypotenuse $=x$

This means we will be using ‘ $CAH$ ‘

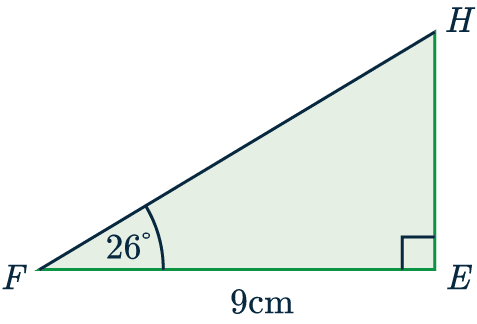
$\cos(26) = \dfrac{\text{Adjacent}}{\text{Hypotenuse}} = \dfrac{9}{FH}$

$FH \times \cos(26) = 9$

$FH = 9 \div \cos(26) = 10.013…$ cm

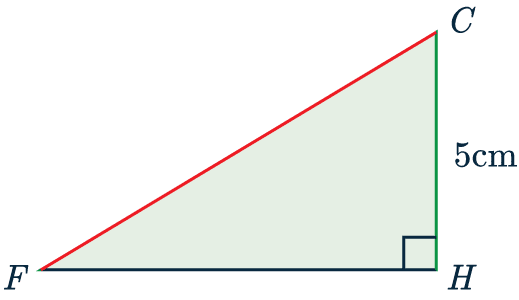
Now we know $FH$ , our first triangle, $FCH$ , looks like this:

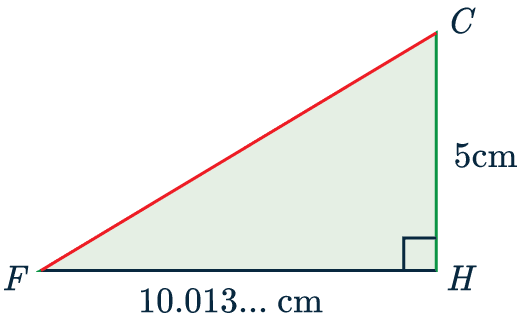
Now, we know two side-lengths of this triangle, we can use Pythagoras’ theorem to find the third, $FC$ , which is the answer to the whole question.

$(FC)^2 = 5^2 + (10.013\dots)^2$

$FC = \sqrt{5^{2} + (10.013…)^{2}} = 11.2$ cm ( $3$ sf).

3D Pythagoras and Trigonometry Example Questions

Question 1: $ABCDE$ is a square-based pyramid. The apex of the pyramid, $E$ , is directly over the centre of the base.

Calculate the perpendicular height of the pyramid. Leave your answer in surd form.

[3 marks]

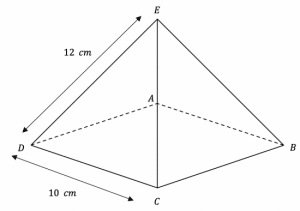
If we draw a line from the apex at $E$ down to the centre of the base, then that line represents the perpendicular height, since we know the apex is directly above the centre. Consider the triangle formed by this line, the line which goes from the centre to $C$ , and the line $EC$ .

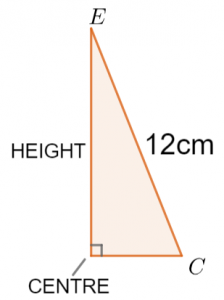
We know the hypotenuse, but we need further information. Here, we observe the distance from the centre to $C$ is half the distance from $A$ to $C$ . Given that we know the width of the square-based triangle, we can find the length of $AC$ , halve it, and then use the result as a part of Pythagoras’ theorem to find the perpendicular height.

For finding $AC$ , consider the triangle $ABC$ .

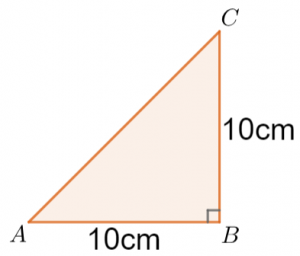
Therefore, the distance from the centre of the base to $C$ is $5\sqrt{2}$ . Finally, we consider again the first triangle, which we now know has base of $5\sqrt{2}$ cm, and calculate the perpendicular height.

$12^2 = (\text{HEIGHT})^2 + (5\sqrt{2})^2$

$(\text{HEIGHT})^2 = 12^2 - (5\sqrt{2})^2 = 144 - 50 = 94$

$\text{HEIGHT } = \sqrt{94}$ cm.

Save your answers with

Gold Standard Education

Question 2: The cuboid shown in the diagram below has the dimensions: $9$ cm by $6$ cm by $12$ cm.

$CY = 6$ cm

Find the length of the line $AY$ .

Leave your answer in surd form.

[2 marks]

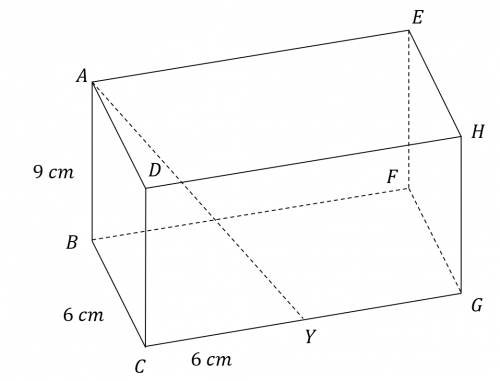
Cuboid Length Question

Here we use $3D$ Pythagoras to find that $AY$ is

$AY^2 =9^2 + 6^2+6^2$

$AY =\sqrt{81+36+36}=\sqrt{153}=3\sqrt{17}$ cm.

Save your answers with

Gold Standard Education

Question 3: The cuboid shown in the diagram below has the dimensions: $9$ cm by $6$ cm by $12$ cm.

Find the length of the diagonal line $CE$ . Leave your answer in surd form.

[2 marks]

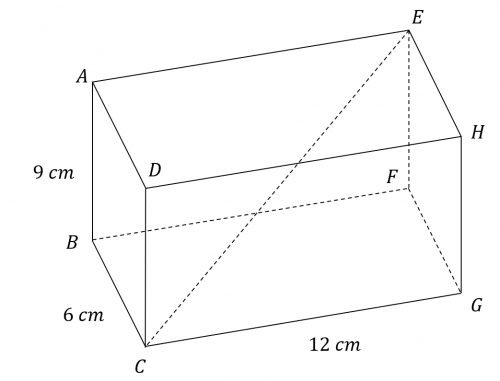
Cuboid Length Question

Here we use $3D$ Pythagoras to find that $CE$ is

$CE^2 =9^2 + 6^2+12^2$

$CE =\sqrt{81+36+144}=\sqrt{261}=3\sqrt{29}$ cm.

Save your answers with

Gold Standard Education

Question 4: $ABCDE$ is a square-based pyramid. The apex of the pyramid, $E$ , is directly over the centre of the base. Calculate the angle $EDB$ . Give your answer to $1$ decimal place.

[3 marks]

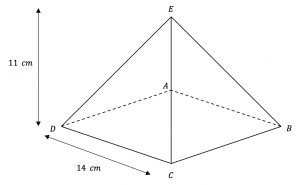
Pyramid Angle Question

First of all, we can work out the length of $DB$ by Pythagoras or by recognizing that the diagonal of a square is $\sqrt{2} \times \text{ side length}$ , thus:

$DB=14\sqrt{2}$

Hence the length from $D$ to the centre of the square, $O$ , is half this value

$DO=7\sqrt{2}$

Now we have enough information to find the required angle,

$\tan(EDB) = \dfrac{O}{A} = \dfrac{11}{7\sqrt{2}}=$

$\text{Angle} \, EDB = tan^{-1} \bigg( \dfrac{11}{7\sqrt{2}} \bigg)=48.0\degree$

Save your answers with

Gold Standard Education